

如何补偿信道对信号带来的高频衰减?
电子说
描述
为了补偿信道对信号带来的高频衰减,发送端通常要求有预/去加重功能,即通过将带有权重pre cursor和post cursor叠加在main cursor上,形成一阶FIR滤波器,从而用其高通的频域特性来补偿信道的低通特性,使信号的质量得到改善。
去加重(De-emphasis):保持信号高频分量不变,减小中低频分量。
预加重(Pre-emphasis):保持信号低频分量不变,增大中高频分量。
去加重补偿后的信号摆幅比预加重补偿后的信号摆幅小,眼图高度低,功耗小,EMC辐射小。
1.FFE
1 **.1 **原理
图1给出了tx发送端框图,包含并串转换(piso)、预驱动(Pre-Drv)、均衡、阻抗匹配。考虑EMC、功耗、摆幅等因素tx端往往采用去加重。
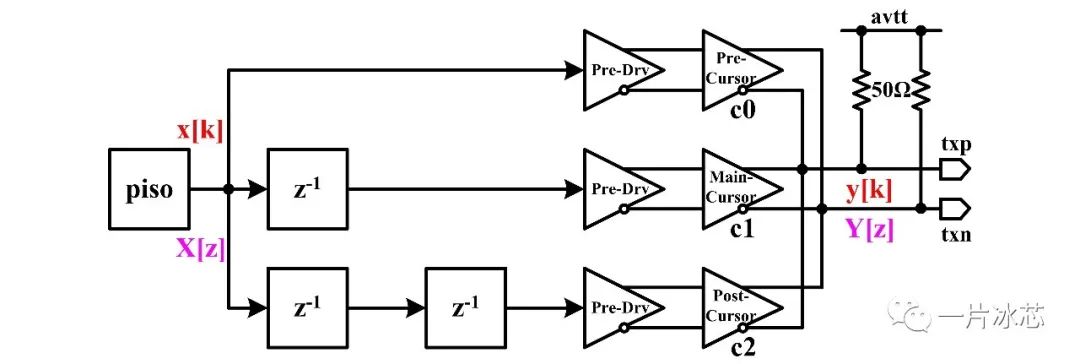
Fig1. tx发送端框图
时域和z域表达式如下:
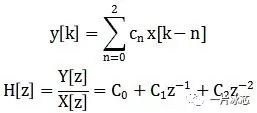
从时域表达式可以看出,当c0或c2为负时,可抑制main cursor上的ISI分量。因此,要想起到补偿,c0和c2可同时为负,也可一正一零,但不能同时为正,c1一定为正。假设c0=-0.1,c1=0.7,c2=-0.2其时域均衡过程如图2所示,可见x[k]经延迟加权再求和可消除输入x[k]上的ISI,经FFE后的波形如图中y[k]。
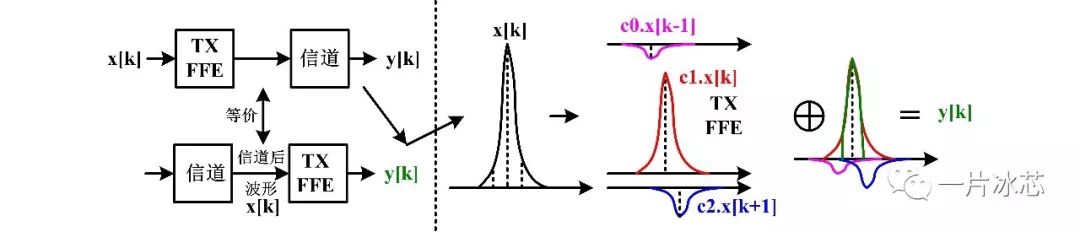
Fig2. FFE时域表示
当c0=-0.1,c1=0.7,c2=-0.2时为去加重,当c0=-0.1,c1=1.3,c2=-0.2时为预加重。
1.2****Matlab验证
用Matlab搭建图3所示的去加重和预加重模型,图中Scope1波形如图4所示,从上到下依次为去加重、输入(111100110101)、预加重波形。可以明显看出去加重可以保持信号高频分量不变,减小中低频分量;预加重可以保持信号低频分量不变,增大中高频分量。
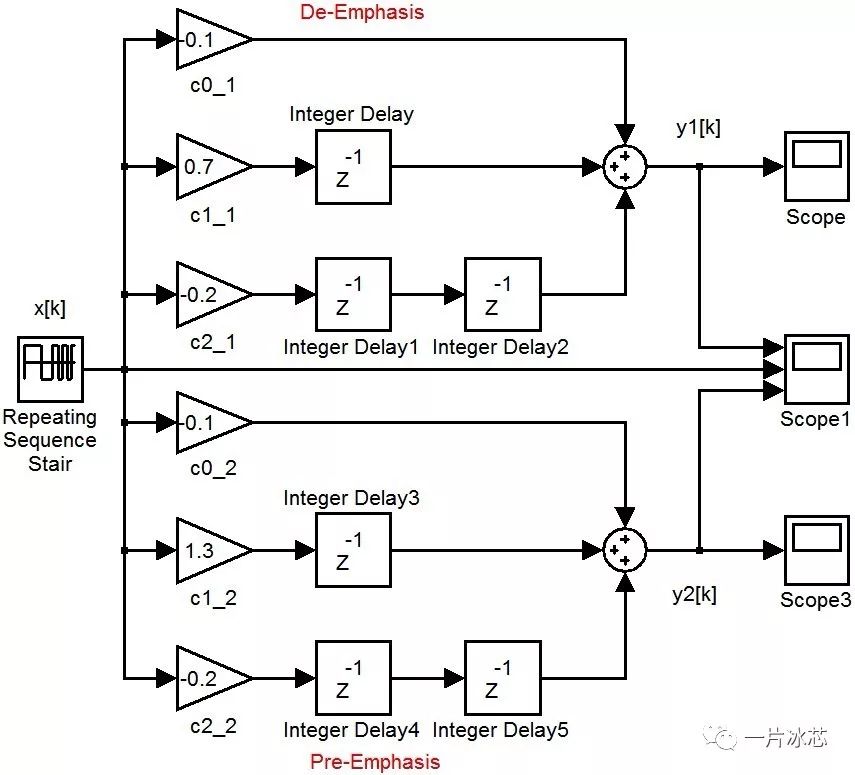
Fig3. Matlab下搭建的De/Pre-Emphasis
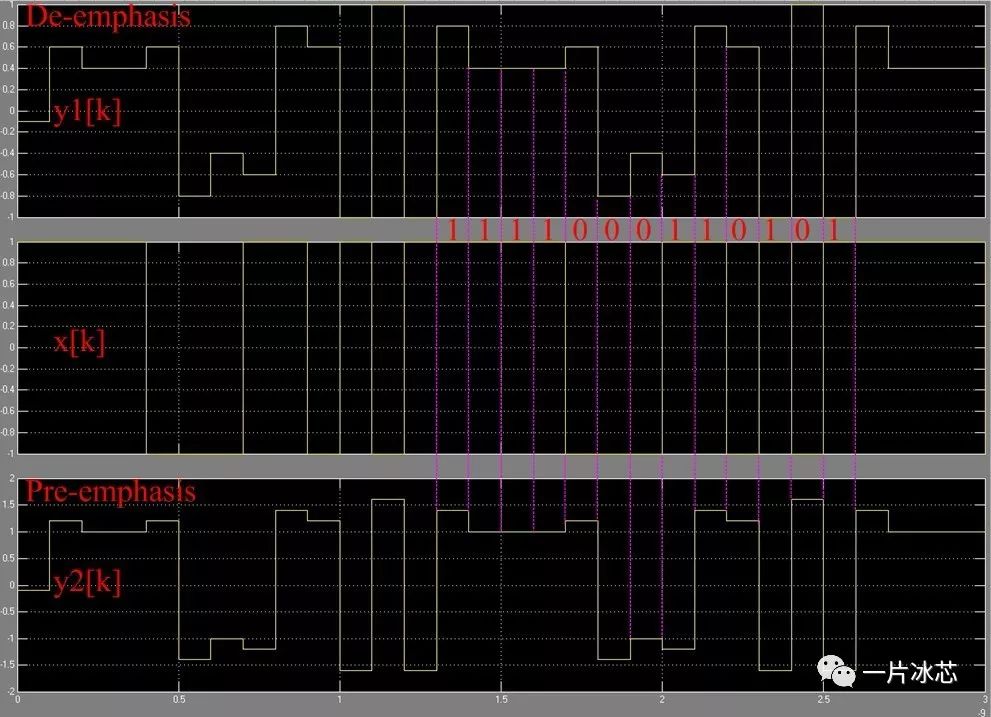
Fig4. 去加重、输入、预加重波形
c0=-0.1,c2=-0.2时去加重(c1=0.7)和预加重(c1=1.3)的0~2π和0~4π的频谱如图5和图6所示。可得出以下结论:①采样频率(fs)位置对应2π,0~π(0~fs/2)之间FIR滤波器呈现高通特性用;②去加重幅度为0.4~1,对信号无放大功能,预加重幅度为1~1.6,可放大信号且在高频下的放大倍数较大。③FFE的频谱以2π为周期进行重复。
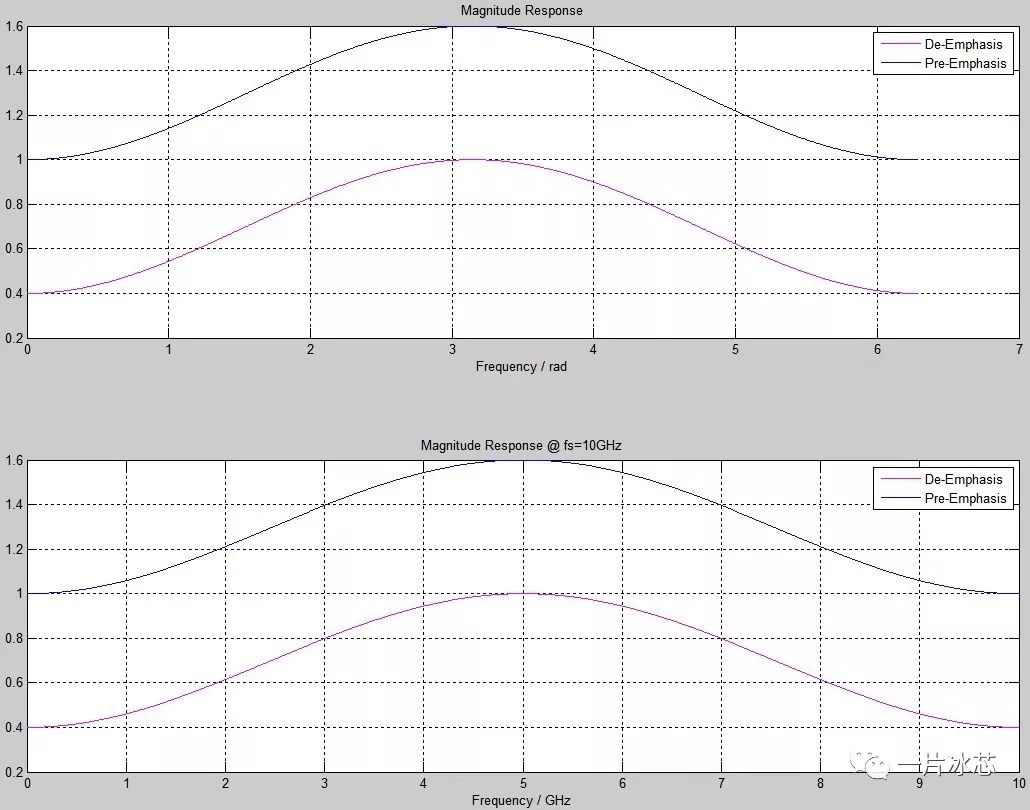
Fig5. 去加重、预加重频谱(0~2π)
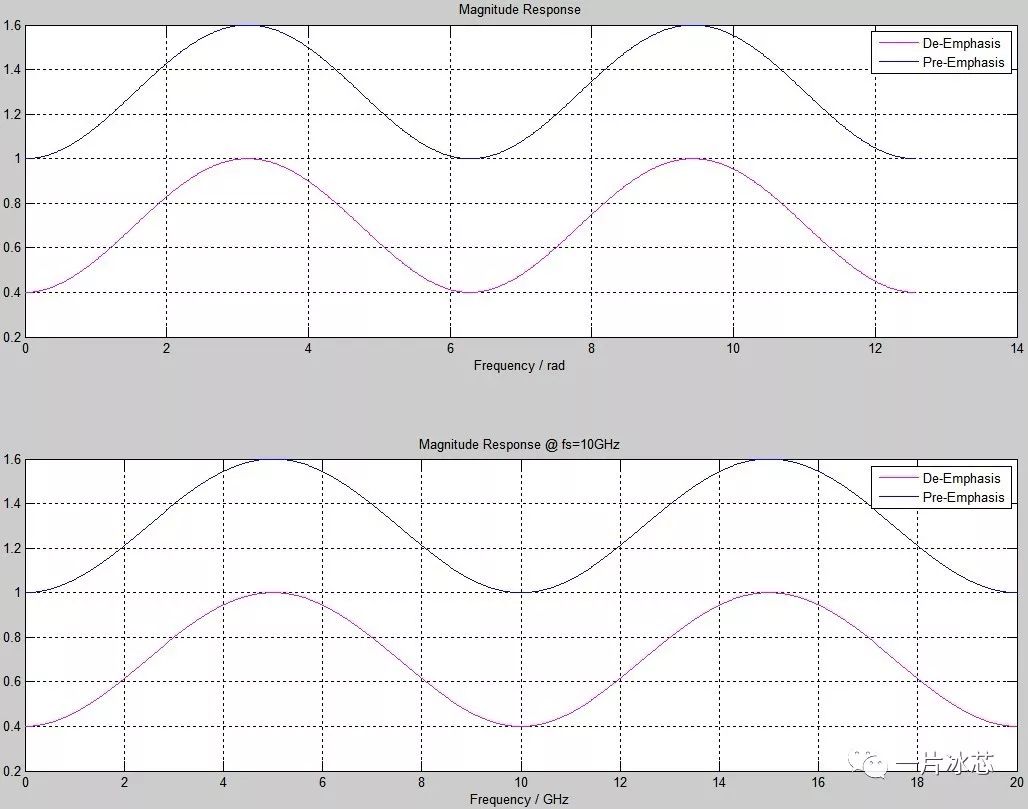
Fig6. 去加重、预加重频谱(0~4π)
计算De/Pre-Emphasis频谱的Matlab Code如下:
clc;
clear all;
close all;
numde = [-0.1 0.7 -0.2];
numpre = [-0.1 1.3 -0.2];
den = [1];
fs=10e9;
w = linspace (0, 2*pi, 1000);
Hde = freqz (numde, den, w);
Hpre = freqz (numpre, den, w);
subplot(2,1,1);
plot (w, abs(Hde),'m-',w, abs(Hpre),'b-');
grid on;
xlabel ('Frequency / rad');
title ('Magnitude Response');
legend('De-Emphasis','Pre-Emphasis');
subplot(2,1,2);
plot (wfs/2/pi/1e9, abs(Hde),'m-',wfs/2/pi/1e9, abs(Hpre),'b-');
grid on;
xlabel ('Frequency / GHz');
title ('Magnitude Response @ fs=10GHz');
legend('De-Emphasis','Pre-Emphasis');
1.3****FIR滤波器系数的计算

ZFS算法Matlab Code如下:
clc;
clear all;
close all;
X=[0.7 0.1 0;0.2 0.7 0.1;0 0.2 0.7]
Xn=X^-1
Y=[0;1;0]
C=Xn*Y
Csigma=(abs(C(1,1))+abs(C(2,1))+abs(C(3,1)))
C0=C(1,1)/Csigma
C1=C(2,1)/Csigma
C2=C(3,1)/Csigma
MMSE算法不强制要求码间干扰在相邻的符号间隔为0,而是使FFE输出端残余的码间干扰的总功率最小,这种算法要优于ZFS。
-
信号衰减的原因和主要影响2023-07-10 14087
-
高频信号衰减,求解??2012-08-24 6008
-
运放放大电路高频衰减问题2015-03-20 5970
-
信号、信道及噪声2008-10-22 452
-
超声衰减增益补偿电路的设计2010-04-27 895
-
信号带宽与信道带宽2009-05-02 4745
-
Labwindows/CVI+Matlab建立高频衰减模型2011-11-22 3553
-
MTVA系列温度补偿衰减器的简单介绍2021-09-03 1892
-
如何延长温度补偿衰减器使用寿命2023-06-28 1351
-
信号完整性-衰减与眼图2023-09-25 3119
-
为什么高频信号不能直接通过电阻的分压来实现信号的衰减呢?2023-10-20 4182
-
传输信号的信道是什么意思?信道的分类 信道在通信中的作用2024-02-01 8292
-
信道对信号的影响可分为哪两类2024-10-15 1995
-
RS485信号衰减的影响及补偿方法2024-11-28 2177
-
高频信号衰减器的工作原理 如何测量衰减器的衰减值2024-12-09 3726
全部0条评论

快来发表一下你的评论吧 !

