机器人柔顺控制系统原理详解

写在前面

理解知识原理 VS 实际用好知识原理，是不同的两码事。原理知识，只是一个因素，不是全部；在用之中，知识只是一个参与者，是一个支撑因素，它既不是目标，也不是全部方法，还不一定是思路的关键。这里涉及到认识论问题：还原论 VS 系统论。分解还原之后，需要用到使用的理论原理知识；但脱离它的局部范围，而进入到整体的系统范围，这是系统论发挥作用的地方。还原的那些单点原理知识需要，但远远不够。而且只理解理论原理，不会穿透它来灵活精巧用之，也等于废知识、死知识。

From 穆博士

对于柔顺控制来说，其核心在于实现整个系统的柔顺交互/接触动力学行为，而不仅局限于阻抗/导纳控制原理和算法。实际上，交互动力学行为受到接触力感知动态、力/位置控制内环动态、环境阻抗不确定性、接触前的速度/加速度，采样延迟效应和关节摩擦力等各种因素影响。从影响交互动力学行为的主导因素这一视角分析，并对硬件实现、工作点（接近速度、加速度等）、算法设计及实现进行系统考虑和统筹，才能实现期望的柔顺控制性能。本文在前文的基础上，进一步对交互动力学行为进行介绍。

从接触不稳定谈起     以导纳控制为例（如图1），导纳控制根据感知到的外力F和导纳控制器对参考位置 x_0进行修正，参考位置减去位置修正量delta_x，生成实际位置指令x_r ，再送入位置控制环路，从而实现柔顺交互。

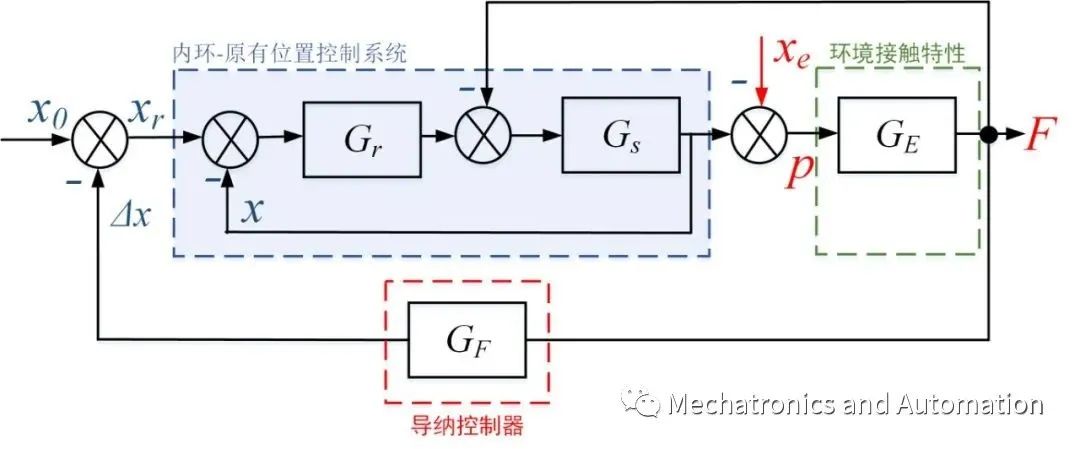
图1. 导纳控制原理

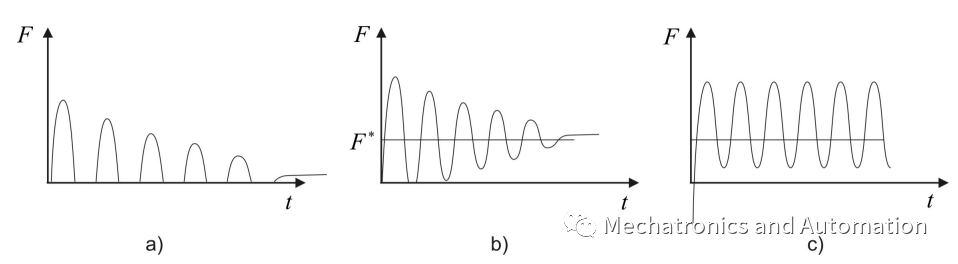
图2. 典型的接触不稳定现象

对于导纳控制，如果环境刚度过大，则在机器人与环境接触时（first impact），将会受到较大的交互力，在位置修正量的作用下，机器人末端将会回退（向脱离接触的方向）。如果阻抗参数设计不合理，位置修正过大，机械臂将会与环境脱离接触，脱离接触后，机械臂回到位置控制模式（此时位置修正量为零），在位置控制模式的作用下，机械臂会再向接触面运动并进行接触，产生交互力，循环往复（bump and then contact lost），相当长的时间内机器人都无法与环境建立接触，甚至会产生过大的冲击力导致机械臂或者接触环境的损害。接触瞬态不稳定现象（contact transition unstability）是机器人柔顺控制系统中首先要避免的问题。

接触瞬态稳定性（contact transient stability）和接触耦合稳定性（ coupled stability）是机器人柔顺控制中极为重要的概念，前者保证是否能够建立接触（一旦建立接触后能一直保持）；后者则定义了建立接触后，接触是否能够稳定（如交互力是否收敛到稳态值）；其中，接触瞬态稳定性是比接触耦合稳定性更为严苛的要求，尤其对于高刚度环境来说（对于刚度相对较小的环境，机器人末端容易透入环境，此时耦合稳定性变为主要矛盾）。根据以上两种接触稳定性概念，可以将接触不稳定现象划分为以下三类（分别如图2a, b, c）：

接触瞬态不稳定，即在首次冲击后接触丢失，然后撞击和脱离接触周期性切换；

接触瞬态不稳定但达到了接触耦合稳定条件，即在首次接触丢失后，在后续过程中，能够实现一个相对稳定接触平衡力（取决于初始接触条件和运动参数，如速度、加速度、参考轨迹，这种情况下也有可能始终无法建立接触，即如情况a）；

接触瞬态稳定但接触耦合处于临界稳定状态，此时接触力出现周期性振荡；

事实上，在柔顺控制系统调试中，由于系统设计不合理或者阻抗参数设计不合理，经常会出现接触不稳定的现象。如桂凯博士在一个实际测试视频中所展示的，当环境接触刚度减小时，柔顺控制就可以从接触不稳定转变为接触稳定。

实际的交互动态

和一般的控制系统分析和控制算法设计类似，柔顺控制中的接触/交互稳定性是一个十分重要的概念，但由于涉及到复杂的理论分析，往往会被人们忽视。当赋予这些理论分析以物理意义时，人们才会开始注意并欣赏稳定性分析的价值。在引入数学工具前，我们需要对实际的接触/交互动态行为从物理直觉上进行描述。不失一般性地，下文分析仍以工业机械臂+导纳控制组成的柔顺控制系统为例，结合图3~5进行说明实际的交互动态。为简化分析，这里限定交互只发生在一个方向，且为单边接触（unilateral contact），其中图3给出了交互过程中涉及的物理量，图4则给出了典型交互过程中（机器人预期轨迹x_0上升-保持两次，最终脱离接触回到原位），各个物理量的变化情况，图5则对接触建立阶段各个物理量变化做了具体说明。

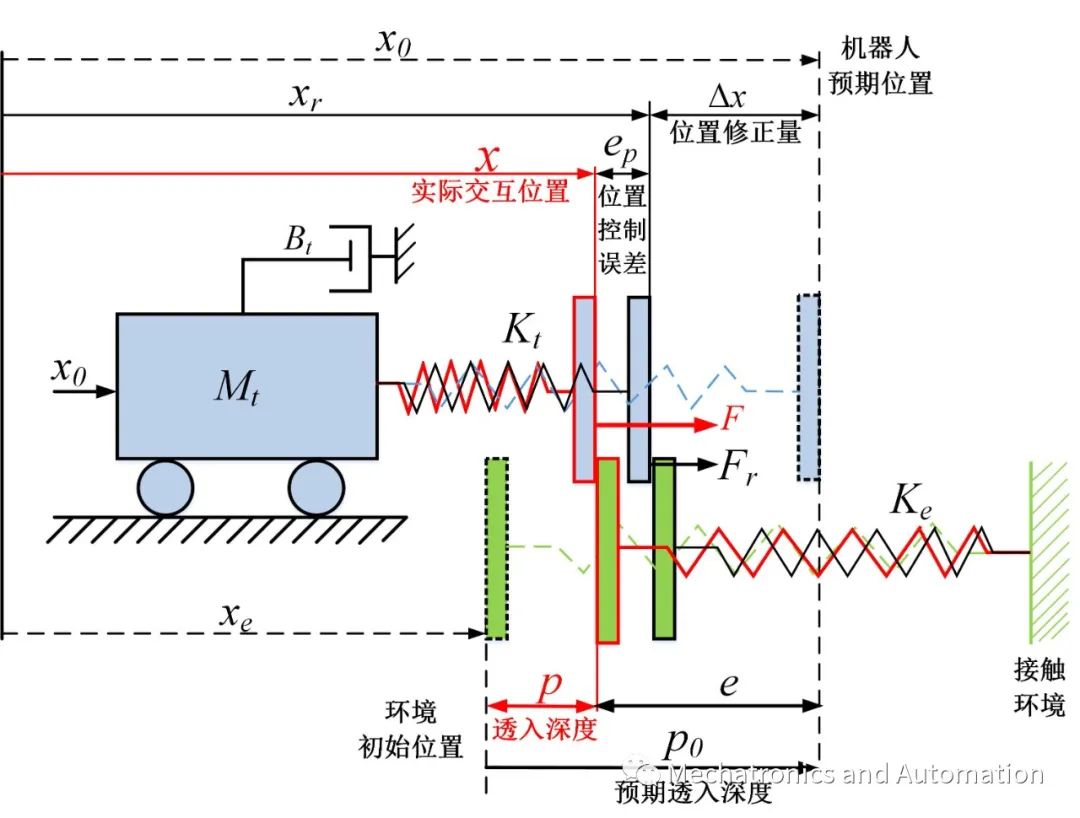
图3. 导纳控制系统等效系统（单自由度）及相关物理量说明

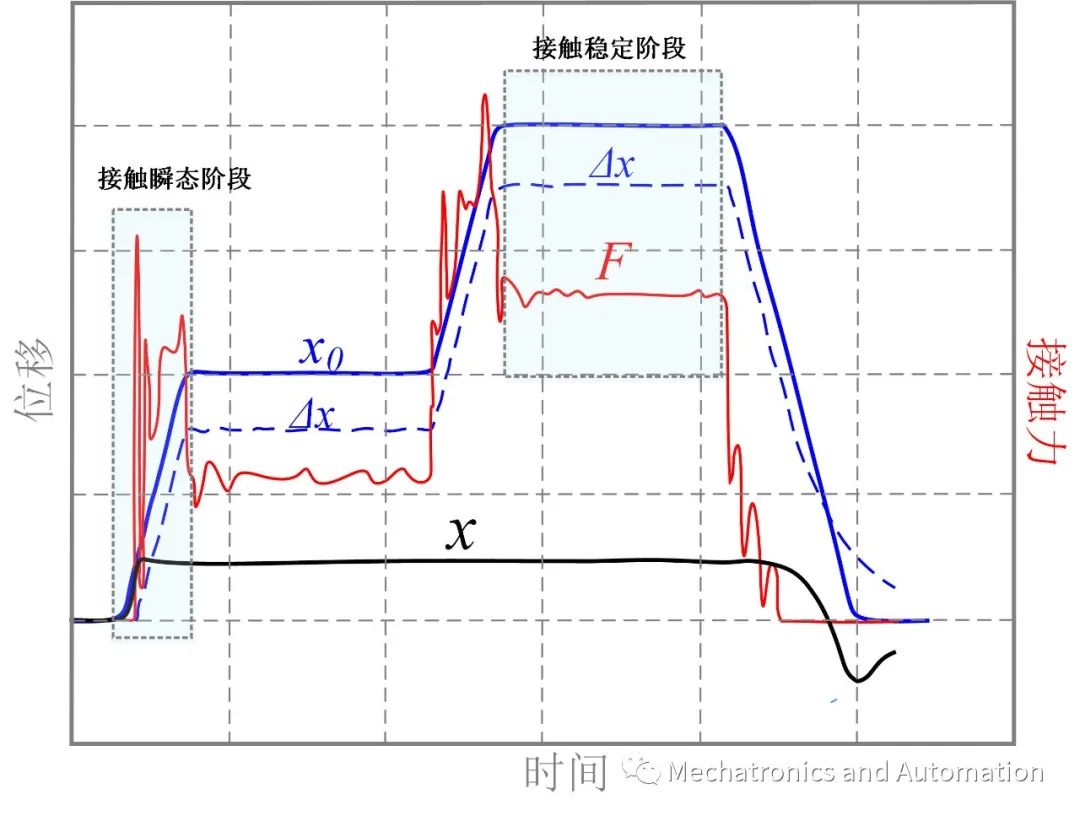
图4. 整个交互过程

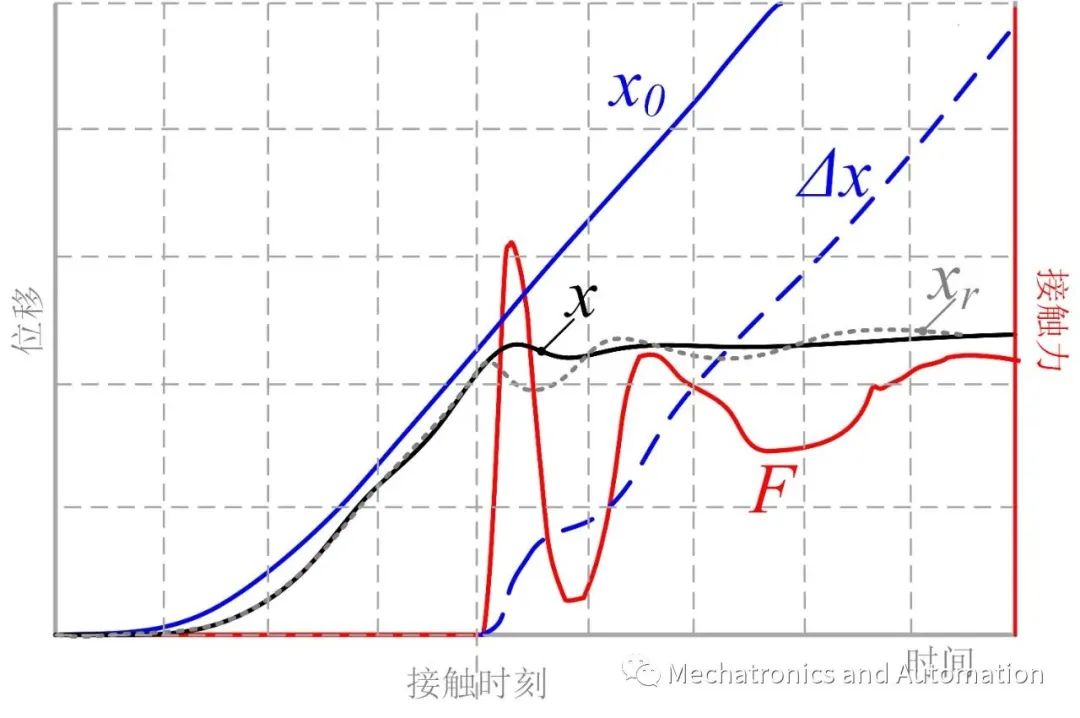
图5、接触建立阶段

在机械臂末端与环境交互过程中，通常可以分为两个阶段-接触建立阶段（或者接触瞬态阶段）和接触稳态阶段。其中在接触建立阶段，各个动态过程如下（参考图5）：

机器人以一定(速度, 加速度)沿轨迹x_0向环境进行移动，由于尚未与环境接触，此时交互力F为0；

机器人继续移动，在环境初始位置x_e处发生接触（此时透入深度为p=x-x_e），在环境刚度K_e作用下，交互力F=K_e*p随之产生，并经过力/力矩传感器（接触力感知动态、采样延迟）送入到柔顺控制系统；

参考图1，感知到的交互力F在导纳控制器G_F的作用下（本质为二阶滤波器，存在一定时延），产生位移修正量delta_x，相应的参考位移x_r随之产生并变化；

位置控制系统接受更新的参考位移x_r，机器人实际位置x 随之发生变化（受位置控制环带宽、位置控制回路非理想因素影响）；

机器人的实际位置x进一步影响着交互位移/透入深度p，透入深度p经环境接触刚度K_e进一步改变交互力F；

值得注意的是，在接触建立阶段，如果系统设计不合理，有可能出现如图2（a）所示的接触瞬态不稳定现象。

当机器人期望轨迹x_0到达设定值后，交互力F 和位移修正量delta_x的稳态值随之确定。然而受限于接触力感知动态、环境阻抗以及实际实现的阻抗（Realized Impedance，受位置控制系统动态和期望阻抗动态综合影响），将会出现交互力F在稳态值附近波动的状态，甚至出现如图2c所示的临界稳定状况。

总结

受限于各个动态因素之间的耦合，柔顺控制系统可能会出现非预期的交互动力学行为，即使对于导纳控制系统这一相对容易实现的柔顺控制方案来说。结合实际物理概念，从系统动力学的角度分析各个因素对动力学行为的影响，然后有针对性地引入数学工具进行理论分析和设计，这一思路对于柔顺控制系统设计和实现来说，仍然是十分重要的。下文将引入接触稳定性的概念，并给出相关的稳定性判据，为避免交互不稳定现象提供理论依据。

以上。

审核编辑：汤梓红