

多元线性回归的特点是什么
描述
何为多元线性回归?对比于前一天学习的线性回归,多元线性回归的特点是什么?
多元线性回归与简单线性回归一样,都是尝试通过使用一个方程式来适配数据,得出相应结果。不同的是,多元线性回归方程,适配的是两个及以上的特征(即X1、X2、...),而简单线性回归一般只有一个特征(X)。
另外,与简单线性回归相比,多元线性回归有一个显著的特点,即能拿到每个特征的权重,这样你能知道哪些因素对结果的影响最大。
请注意多元线性回归的以下4个前提:
1.线性:自变量和因变量的关系应该大致呈线性的。
2.呈现多元正态分布。
3.保持误差项的方差齐性(误差项方差必须等同)。
4.缺少多重共线性。
第一、二点比较好理解,第三、四点需要详细地讲一下:
第三点,保持误差项的方差齐性的意义 : 首先,明确什么叫误差项?误差项也可以叫随机误差项,一般包括:
1)模型中省略的对被解释变量(Y)不重要的影响因素 (解释变量(X));
2)解释变量(X)和被解释变量(Y)的观测误差;
3)经济系统中无法控制、不易度量的随机因素。
再确定什么叫 方差齐性 :顾名思义,方差相等。与什么东西的方差呢?这里需要引入残差的概念:残差,即预测值和真实值之间的差值。而方差齐性,指的就是满足随机分布的残差,如下图所示:
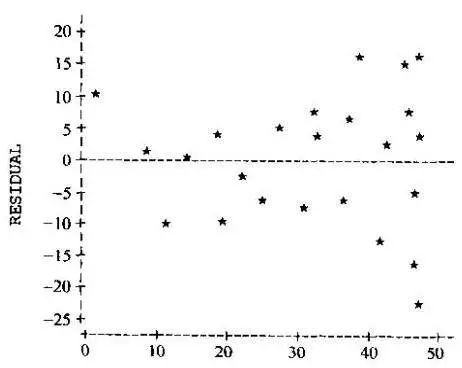
如何判断数据是否满足方差齐性呢?精确的判断是很难做到的,我们可以通过上图绘制X值与残差的关系来大致估计,也可以用一个巧妙的方法: 对残差做简单线性回归,如果得到的直线大致平行于X轴,则说明满足方差齐性 。
这种观察自变量与残差之间是否存在线性关系(BP法)或非线性关系(White检验)是较为常用的两种方差齐性检验的方法。
第四点,缺少多重共线性的意义 :根据回归分析的结果,一般而言我们能发现自变量X1、X2、... 等因素对Y的影响。但是存在一种情况:如果各个自变量x之间有很强的线性关系,就无法固定其他变量,也就找不到x和y之间真实的关系了,这就叫做多重共线性。
有多种方法可以检测多重共线性,较常使用的是回归分析中的VIF值(方差膨胀因子),VIF值越大,多重共线性越严重。VIF怎么计算? VIF=1/(1-R^2) , 其中R^2是样本可决系数。样本可决系数怎么计算?答案是通过残差,这里有详细的计算方法:

一般认为VIF大于10时(严格是5),代表模型存在严重的共线性问题。
讲了这么多理论知识,大家可能觉得比较枯燥,但是实际上本文最难的也就是这些理论知识,希望大家能好好消化。下面正式开始实操部分。
1.准****备
开始之前,你要确保Python和pip已经成功安装在电脑上,如果没有,请访问这篇文章:超详细Python安装指南 进行安装。
如果你用Python的目的是数据分析,可以直接安装Anaconda:Python数据分析与挖掘好帮手—Anaconda,它内置了Python和pip.
此外,推荐大家用VSCode编辑器,因为它有许多许多的优点:Python 编程的最好搭档—VSCode 详细指南。
准备输入命令安装依赖,如果你没有VSCode编辑器,Windows环境下打开 Cmd (开始-运行-CMD),苹果系统环境下请打开 Terminal (command+空格输入Terminal),如果你用的是VSCode编辑器或Pycharm,可以直接在下方的Terminal中输入命令:
pip install pandas
pip install numpy
pip install matplotlib
pip install scikit-learn
本篇文章使用的50_Startups.csv文件,由研发开销、管理开销、市场开销、州和利润五列数据组成。
本文源代码和数据文件,可以关注Python实用宝典公众号,后台回复:**机器学习3 **下载。
2.数据预处理
导入库
import pandas as pd
import numpy as np
导入数据集
最后一列利润为Y值,其他均为X值。
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[:, :-1].values
Y = dataset.iloc[:, 4].values
将类别数据数字化
将“州”这一列数字化。
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[:, 3] = labelencoder.fit_transform(X[:, 3])
# 一共有3个州
onehotencoder = OneHotEncoder(categorical_features=[3])
X = onehotencoder.fit_transform(X).toarray()
躲避虚拟变量陷阱
原始数据如下:
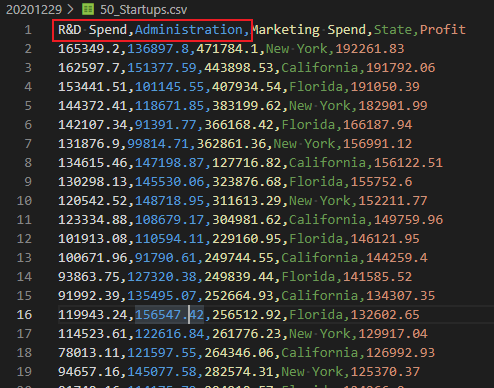
在我们对“州”这列变量进行数字化后,会在前面出现三列one_hot变量,每一列代表一个州。
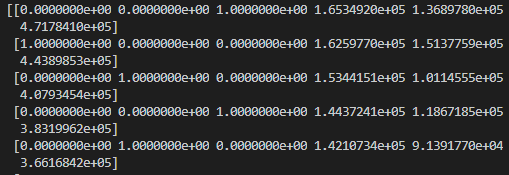
这就出现虚拟变量陷阱了,比如第一列我们能通过另外两列的值得到:如果2、3列为0,第1列肯定为1,如果2、3列存在不为0的值,则第1列肯定为1。
因此,这里第一列没有使用的必要。
X = X[: , 1:]
拆分数据集为训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state = 0)
3. 训练模型
与简单线性回归一样,使用LinearRegression即可实现多元线性回归(sklearn已经帮你处理好多元的情况)。
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, Y_train)
4. 预测结果
一行搞定:
y_pred = regressor.predict(X_test)
print("real:", Y_test)
print("predict:", y_pred)
看看效果:

画个图看看对比效果:
map_index = list(range(len(Y_test)))
plt.scatter(map_index, Y_test, color='red')
plt.plot(map_index, y_pred, color='blue')
plt.show()
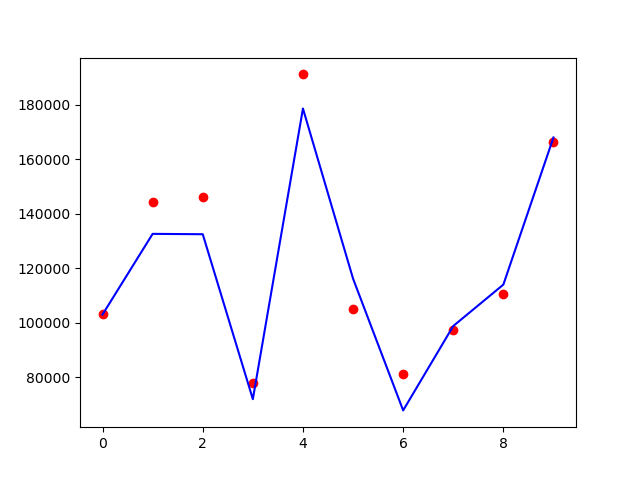
蓝色的线是预测值,红色的点是真实的值,可以看到预测效果还是不错的。
-
基于RK3568国产处理器教学实验箱操作案例分享:一元线性回归实验2024-12-05 1628
-
如何用C语言实现一个简单的一元线性回归算法2021-07-20 1614
-
TensorFlow实现简单线性回归2020-08-11 1898
-
回归算法有哪些,常用回归算法(3种)详解2020-07-28 2615
-
Multivariate Linear Regression多变量线性回归2020-06-11 1224
-
Tensorflow的非线性回归2020-05-12 1722
-
生产应用中使用线性回归进行实际操练2020-05-08 1072
-
线性回归定义2019-09-03 1226
-
线性回归的标准方程法使用2019-05-07 2003
-
最小二乘多元线性回归及Mie光散射便携式扬尘粒子监测系统的资料概述2018-11-20 1458
-
基于Weierstrass逼近定理在非线性回归模型中应用2018-01-12 820
-
基于多元线性回归的阻性和容性电流分解2017-01-07 551
-
matlab回归分析总结2012-03-20 12022
全部0条评论

快来发表一下你的评论吧 !

