

Python在函数方向导数计算中的应用
描述
方向导数是在函数f(x)在某一点沿着特定方向的变化率。假设我们有一个多维空间中的函数f(x, y, z),并且我们想要在点(x0, y0, z0)沿着向量(dx, dy, dz)的方向导数。
函数方向导数的计算步骤如下:
- 找到函数在某点处的梯度向量(gradient vector)或方向导数向量(directional derivative vector);
- 确定一个方向向量,这个向量是从函数在某点处的切线向量到需要计算的方向导数的点的向量;
- 将两个向量进行点积运算,得到的就是函数在该点处沿着这个方向向量的方向导数;
- 如果这个方向向量有多个分量,需要将它们分别对应到梯度向量的分量上进行点积运算,然后将得到的所有值相加即可得到最终的结果。
以下是一个使用Python计算方向导数的简单示例。
import numpy as np
# 定义函数 f(x, y, z) = x^2 + y^2 + z^2
def func(x, y, z):
return x**2 + y**2 + z**2
# 定义点 (x0, y0, z0)
x0, y0, z0 = 1.0, 2.0, 3.0
# 定义方向向量 (dx, dy, dz)
dx, dy, dz = 0.1, 0.2, 0.3
# 为了计算方向导数,我们需要计算函数在点 (x0, y0, z0) + t * (dx, dy, dz) 的值
# 然后求导数,即 t = 0 时的导数值
t = np.linspace(0, 0, 1) # 创建一个包含单个元素0的数组,以便在t=0处求导
points = np.array([x0 + t[0] * dx, y0 + t[0] * dy, z0 + t[0] * dz]) # 生成点集
values = np.array([func(point[0], point[1], point[2]) for point in points]) # 计算函数值
# 使用numpy的gradient函数计算导数
derivatives = np.gradient(values) # 这将返回一个数组,其中第一个元素是函数值对t的导数
directional_derivative = derivatives[0] # 取导数的第一个元素,即t=0处的导数
print(f"Directional derivative at point ({x0}, {y0}, {z0}) in direction ({dx}, {dy}, {dz}) is: {directional_derivative}")
在这个例子中,函数f(x, y, z) = x^2 + y^2 + z^2在点(1.0, 2.0, 3.0)沿着方向(0.1, 0.2, 0.3)的方向导数为:
Directional derivative at point (1.0, 2.0, 3.0) in direction (0.1, 0.2, 0.3) is: 5.7345137877764745
这段代码计算的就是函数f(x, y, z)方向导数。
下面给出计算并绘制函数x^2+y^2的方向导数的Python代码。
import numpy as np
import matplotlib.pyplot as plt
# 定义函数
def f(x, y):
return x**2 + y**2
# 定义方向导数函数
def directional_derivative(x, y, direction):
h = 0.0001
return (f(x + h*direction[0], y + h*direction[1]) - f(x, y)) / h
# 定义图形绘制函数
def plot_derivative(x, y, direction, xlabel, ylabel, title):
dx, dy = direction
derivative = directional_derivative(x, y, [dx, dy])
plt.figure(figsize=(10, 6))
plt.plot(dx, dy, 'ro') # 绘制方向向量
plt.quiver(0, 0, dx, dy, angles='xy', scale_units='xy', scale=1) # 绘制向量场
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.grid(True)
# 使用例子
x = 1
y = 1
direction = [1, 1] # 任意方向
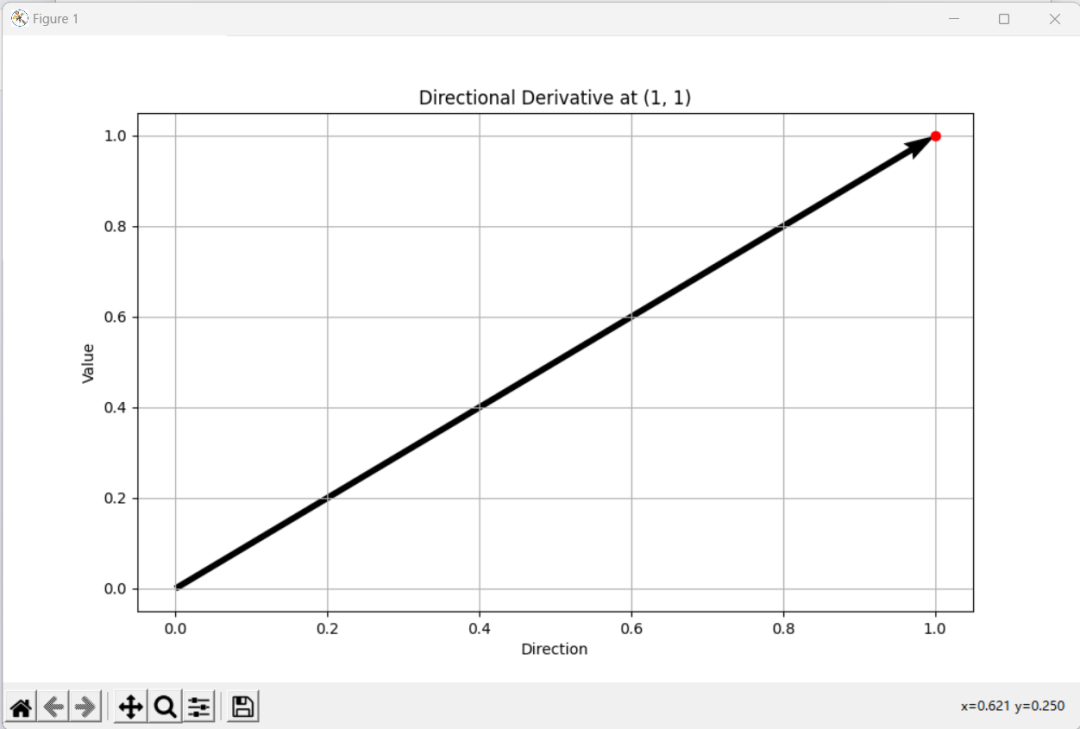
plot_derivative(x, y, direction, 'Direction', 'Value', 'Directional Derivative at ({}, {})'.format(x, y))
plt.show()
在上述代码中,首先定义了函数f(x, y),然后定义了一个计算方向导数的函数directional_derivative。接着定义了一个用于绘制方向导数的函数plot_derivative,该函数使用matplotlib库绘制方向向量和向量场,并显示方向导数的值。在主程序部分,选择了函数f(x, y)上的一点(1, 1)和一个方向[1, 1],并调用了plot_derivative函数来显示该点的方向导数。
这短代码在运行时应该显示一个图形,其中包括从原点出发的向量和一个箭头,箭头的方向表示函数在给定方向上的变化率最大的方向。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
python中open函数的用法详解2024-01-30 3600
-
不属于python的内置函数2023-11-29 2198
-
复数中i在Python中如何定义2023-11-22 4583
-
Python 梯度计算模块如何实现一个逻辑回归模型2023-10-21 1055
-
python定义函数与调用函数的顺序2023-10-04 2572
-
深入了解WinDaq导数算法2022-12-05 1228
-
在Python中实现更简单好用的函数运算缓存2022-08-05 1469
-
怎么在python中执行函数2022-03-29 2656
-
基于布尔函数导数的布尔置换构造2021-06-17 852
-
Python十大应用领域和就业方向2018-11-21 4340
-
学习Python的发展方向2018-04-02 7946
-
学python有哪些方向?2018-03-09 4717
-
从方向导数这个角度来解析梯度的负方向为什么是局部下降最快的方向2018-02-05 10354
全部0条评论

快来发表一下你的评论吧 !

