

用Python实现矩阵与线性变换
描述
认识矩阵
矩阵是向量的集合,把多个向量组织在一起就构成了一个矩阵。例如在三维空间内,有A、B、C三个向量。
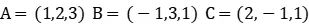
将A、B、C三个向量按照行的方式组织在一起构成了矩阵M:

将A、B、C三个向量按照列的方式组织在一起构成了矩阵T:

矩阵M的向量称为行向量,矩阵T的向量称为列向量。下面给出矩阵的定义:
矩阵是由m X n个数aij排列成的m行n列的数表,称为m行n列矩阵,简称m X n 矩阵。矩阵表示如下:

在上述定义中,可以把矩阵A看作是由m个:

向量构成的。
如果矩阵的行和列相同,即矩阵是由n X n个数aij排列成的n行n列的数表,称为n阶矩阵。
矩阵的转置运算
前面的矩阵M和矩阵T可以互相转换,这种转换称为矩阵的转置运算。矩阵的转置就是把矩阵的行列互换,行变成列,列变成行。例如对M矩阵行列互换后,就构成了矩阵T。
下面给出矩阵的转置概念:
把m X n矩阵A的行列依次互换得到n X m矩阵,称为矩阵A的转置矩阵,记作AT。

矩阵的转置运算满足下面的运算律:
(AT)T = A
转置矩阵的转置矩阵是原矩阵。
(A + B)T = AT + BT
A与B和的转置矩阵等于A的转置矩阵与B的转置矩阵的和。
(AB)T = BTAT
A与B矩阵积的转置矩阵等于B的转置矩阵与A的转置的积(顺序不能颠倒)。
矩阵的加法运算
设有矩阵A和矩阵B:

如何计算A+B和A-B呢?
两个矩阵进行加法和减法运算有一个前提条件,就是两个矩阵的行数和列数相同,在这种情况下,两个矩阵相加和相减的结果是一个新的矩阵,新矩阵的行数和列数和原来矩阵的行列数相同,其元素分别是两个矩阵对应元素的和值和差值。


矩阵的加法和减法运算可以看作矩阵内对应向量的加法或减法运算。例如在计算A+B的过程中,A的列向量或行向量分别与B的列向量或行向量相加,结果是新矩阵的列向量或行向量。
纯量与矩阵的乘法运算
纯量与矩阵相乘,结果矩阵与原矩阵的行列数相同,其元素的值是原矩阵中每个对应元素与纯量相乘的数值。
(-1)* B的计算过程如下所示:

例1:编写Python程序,实现前面矩阵A和B的加法运算和减法运算。
在Python程序中,使用嵌套列表定义一个二维数组,这个二维数组就是一个矩阵。
#使用嵌套列表定义矩阵A和B
A = [[-1,3,2],[5,7,-2],[-3,0,1]]
B = [[8,2,-1],[6,4,0],[-2,3,5]]
#定义矩阵C,存储A+B的结果
C = [[0,0,0],[0,0,0],[0,0,0]]
#定义矩阵D,存储A-B的结果
D = [[0,0,0],[0,0,0],[0,0,0]]
遍历A矩阵的行
for i in range(len(A)):
遍历A矩阵的列
for j in range(len(A[0])):
C[i][j] = A[i][j] + B[i][j]
D[i][j] = A[i][j] - B[i][j]
print(C)
print(D)
在实际应用中,一般使用numpy对矩阵进行运算。
导入numpy模块
import numpy as np
定义矩阵
A = np.array([[-1,3,2],[5,7,-2],[-3,0,1]])
B = np.array([[8,2,-1],[6,4,0],[-2,3,5]])
矩阵运算
print(A+B)
print(A-B)
矩阵的线性变换
变换本质是一个函数,它是一个映射,它接受输入内容并输出对应结果。
例如函数:

当x取不同实数时,都会有唯一对应的输出结果来对应输入的x。
对线性代数来说,变换是接受一个向量,并输出一个向量。在线性代数中,一个向量到另外一个向量的映射之所以称为变换,不称为函数,是因为考虑到了向量的变换实际是向量的运动。
如:二维空间的向量A到向量B的变换,实际是向量A通过变换移动到了向量B的位置。
A =(10,0,60.0) B=(56.6,22.3)

图中向量A到向量B的变换是一种旋转变换,该变换为线性变换,它满足下面的性质。
设旋转变换为T,对线性空间V中的任意向量A和B及实数k,均有
T(A+B)= T(A)+T(B)
T(kA) = kT(A)
要验证旋转变换是否是线性变换,需要求出变换T,看变换T是否满足线性变换的两个性质。下图是二维空间向量V围绕原点逆时针旋转的示意图。

如上图所示,向量V绕原点逆时针旋转θ角,得到向量V’,假设向量V=(x,y),则向量V’为:

旋转变换T为:

若T是线性变换,应满足线性变换的两个性质。下面我们用Python程序来验证T是线性变换。验证代码如下:
import numpy as np
# 定义向量A
A = np.array([3,2])
# 定义向量B
B = np.array([-1,5])
# 定义纯量K
k = 3.14
# 定义旋转角度
r = 30
# 定义变换T函数
# v:向量 a:旋转的角度
def T(v,a):
# 转换为弧度
a = a / 180 * np.pi
# 向量v旋转a到m
m = np.array([v[0]*np.cos(a)-v[1]*np.sin(a),
v[0]*np.sin(a)+v[1]*np.cos(a)])
return m
print("T(A+B)=T(A)+T(B):%s:%s" % (str(T(A+B,r)),str(T(A,r)+T(B,r))))
print("kT(A)=T(kA):%s:%s" % (str(k*T(A,r)),str(T(k*A,r))))
输出结果如下图所示:

旋转变换T可以用矩阵表示,T也称为旋转变换矩阵:

计算向量V到向量V’的转换可以使用矩阵乘法:

使用矩阵乘法可以对多个二维向量组进行旋转:

Python代码如下:
import numpy as np
#定义旋转矩阵T
# a:旋转角度
def T(a):
# 转换为弧度
a = a / 180 * np.pi
return np.array([
[np.cos(a),-np.sin(a)],
[np.sin(a),np.cos(a)]
])
# 定义矩阵A
# 矩阵A为待旋转的向量组
A = np.array([[3,2],
[-1,5],
[5,-2],
[2,-3],
[1,-1]
])
# 对矩阵A进行转置再相乘
C = np.matmul(T(30),np.transpose(A))
print(C)
输出结果如下图所示:

-
滤波器设计与信号处理的MATLAB实现2023-09-26 589
-
变换矩阵无法实现正常变换2021-08-27 1225
-
如何用双线性变换法来设计数字滤波器?2021-04-12 1465
-
西门子PLC模拟量线性变换子程序的编写2020-03-19 7261
-
基于Matrix矩阵变换的图形变换技巧分享2017-09-06 964
-
传递函数 2.3状态空间表达式的建立 2.4线性变换2016-12-13 886
-
模拟信号线性变换该如何设计2015-03-25 3051
-
双线性变换法中预畸变概念的补充2011-04-07 1230
-
a稳定分布噪声中谐波恢复的非线性变换方法2010-01-12 583
-
用双线性变换法设计IIR滤波器2009-05-10 1692
-
Stein方程的线性变换解法2008-12-10 858
-
设计IIR滤波器的双线性变换法2008-08-01 5377
全部0条评论

快来发表一下你的评论吧 !

