异步FIFO设计之格雷码

     相邻的格雷码只有1bit的差异，因此格雷码常常用于异步fifo设计中，保证afifo的读地址（或写地址）被写时钟（或读时钟）采样时最多只有1bit发生跳变。

在不考虑路径延时的情况下，因为源数据（读写地址）只有1bit变化，即使发生了亚稳态，最终的结果相当于被目的时钟延迟一拍采样。

需要注意的是：异步fifo中使用格雷码无法避免亚稳态，它起到的作用是，即使发生了亚稳态，依旧能够保证异步fifo的功能正确        

10进制	二进制	格雷码
0	000	000
1	001	001
2	010	011
3	011	010
4	100	110
5	101	111
6	110	101
7	111	100

1.二进制转格雷码   

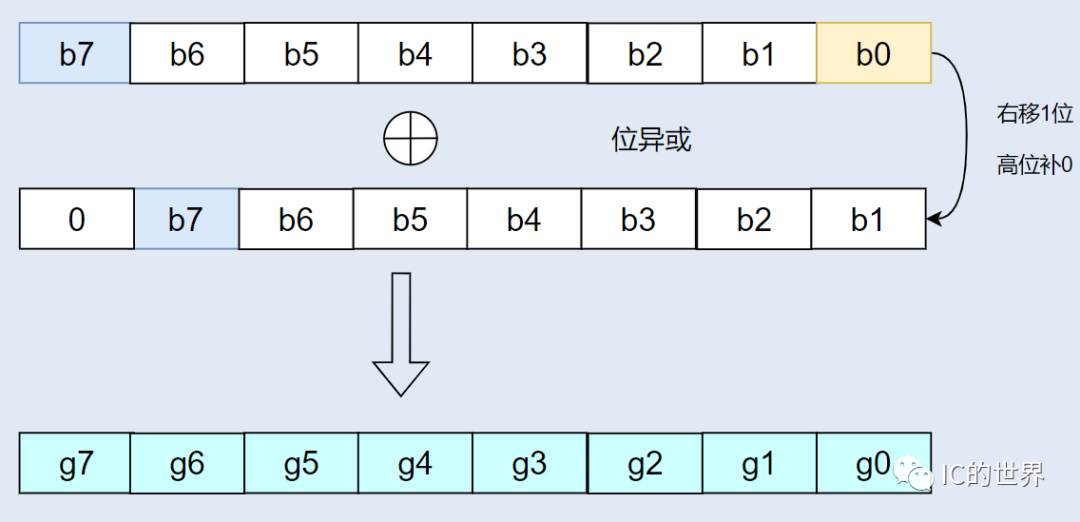图1：二进制转格雷码

如图所示，二进制转格雷码实现简单，二进制数据右移1bit，高位补零后与自身进行位异或得到格雷码。代码实现如下：waddr为二进制写地址，waddr_gray为对应的写地址格雷码
 

assign waddr_gray[ADDR_WDTH:0]=waddr[ADDR_WDTH:0] ^ {1’b0,waddr[ADDR_WDTH:1] }；      

 

2.格雷码转二进制  

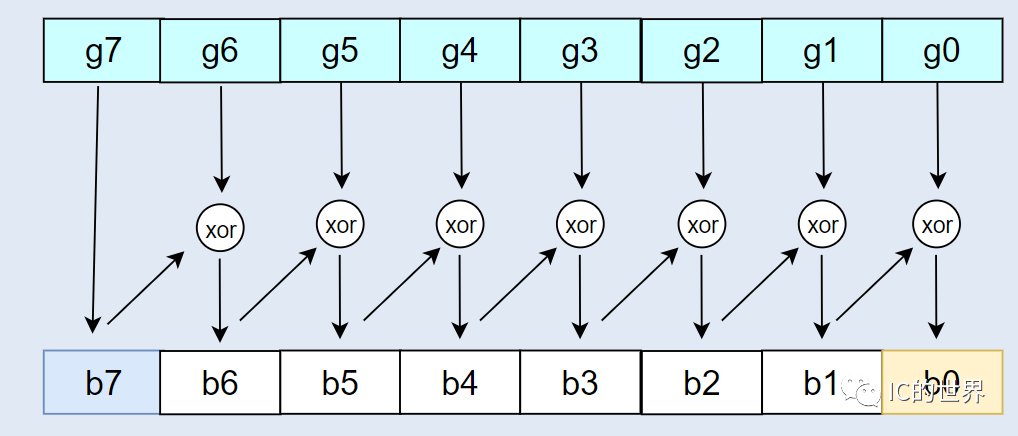
图2：格雷码转2进制 首先需要强调一下异或操作的特点：

  A、B、C为1bit二进制整数，假设等式为A^B==C，那么已知B和C的情况下，可以通过A==B^C求得A数值。此处可以使用穷举法尝试一下，只有4种情况。  

 


从二进制转格雷码也可以反推出格雷码转二进制的思路。

首先：最高bit位是相等的，b7等于g7。

因为g6==b7^b6，根据异或特性（由A^B==C得到A==B^C），可得知b6=b7^g6，即b6=g7^g6

因为g5==b5^b6，根据异或特性，可得知b5=g5^b6，即b5=g5^g6^g7

依次类推:b0=g0^g1^g2^g3^g4^g6^g7        

 

在如下Verilog代码实现中，我们提供了3种写法。
写法1和写法2都是已知确定位宽的情况下，实现格雷码转二进制码，不利于参数化。

写法3采用function函数实现，不限制位宽，支持参数化。   

 

//写法 1


assign bin_code[0]=gray_code[0]^gray_code[1]^gray_code[2]^gray_code[3] ;
assign bin_code[1]=gray_code[1]^gray_code[2]^gray_code[3] ;
assign bin_code[2]=gray_code[2]^gray_code[3] ;
assign bin_code[3]=gray_code[3] ;




//写法2
assign bin_code = {gray_code[3], ^gray_code[3:2], ^gray_code[3:1], ^gray_code};






//写法3：
function       [ADDR_WIDTH:0]   bin_out;    
   input       [ADDR_WIDTH:0]   gray_in;    
   reg         [ADDR_WIDTH:0]   gray_code;  
   reg         [ADDR_WIDTH:0]   bin_code;   
   integer i,j;                             
   reg tmp;                                 
   begin
       gray_code = gray_in;
       for(i=0;i<=ADDR_WIDTH;i=i+1)
           begin
           tmp=1'b0;
           for(j=i;j<=ADDR_WIDTH;j=j+1)
              tmp=gray_code[j]^tmp;
           bin_code[i]=tmp;
           end
       bin_out= bin_code;
   end
endfunction 

         

 

　　审核编辑：汤梓红