一文详解正弦交流电路的基础知识

4.1 正弦量

一、时变电压和时变电流

时变电压和时变电流：随时间不断变化的电压和电流。

瞬时值：时变电压和时变电流在任一时刻的数值，用 u(t)和i(t) 来表示，解析式是一个时间函数。

图1

周期量：每个值在经过相等的时间间隔后循环出现的时变电压和电流，对应周期性函数。这个最小的相等的时间间隔称为周期，一般用符号T来表示。周期的倒数称为频率，用f来表示；

称为角频率

图2

交变量：考虑一个周期内波形面积平均值为零的时变电压或时变电流。

图3

二、正弦量的三要素

正弦量：随时间按照正弦（余弦）规律变化的交流量，解析式是一个正弦函数表达式。

设正弦电流

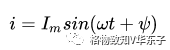
正弦量的三要素：幅值(决定大小)、角频率（决定变化快慢）、初相位（决定初始位置）。

1.幅值：交流电的最大瞬时值称为幅值或最大值，如 Im 。幅值必用大写字母下标加 m来表示。

表征正弦量变化快慢的三个参数：

①周期 T：变化一周所需的时间。单位：秒(s)

②频率 f：每秒变化的次数。单位：赫兹(Hz)

③角频率ω：每秒变化的弧度。单位：弧度/秒(rad/s)

三者间的关系：

电网频率（工频）：我国：50Hz；美国和日本：60Hz 无线通信频率：30 kHz ～ 30GMHz

相位和初相位:

三、相位差

1.相位差 φ ：两个同频率正弦量间的相位之差，即初相位之差。

2.两个正弦量的相位关系

需要强调的是：对不同频率的正弦量进行比较没有意义。两个同频率正弦量之间的相位差为常数，和频率以及计时起点的选择无关。

规定：相位差的绝对值不超过π。

四、正弦量的有效值

1.有效值：如果一个周期电流 i 通过一个电阻 R , 在一个周期 T 内消耗的热能等于直流电流 I 在同样时间内通过该电阻 R 消耗的能量 , 则I 定义为 i 的有效值。用无下标的大写字母表示。

2.正弦量的有效值与最大值关系

一般交流电压表和电流表测量的数据均为有效值；无特殊说明，交流设备铭牌标注的电压、电流也是有效值。

对于正弦交流电路，电路中各部分的电压、电流瞬时大小都是随时间按照正弦规律变化的。我们在中学学过正弦函数的运算，在时域里，正弦量的加减乘除是非常麻烦的，不利于对正弦交流电路的分析。另外，对于电感、电容这样的储能元件伏安特性要用微分形式，电路的时域方程是微分方程。微分方程求解，即使是一阶、二阶微分方程都太难了，更不要讲高阶微分方程。

科学们想到了一种方法，那就是相量法，用一个复数（相量）来表示一个正弦量，将电路的时域形式映射到频域。在频域里，正弦交流电路的方程是代数方程，运算就变成了复数运算（相量运算），我们可以使用初等方法了；来分析电路，从而大大简化了电路分析的过程。

电感和电容的阻抗就是应用相量法得到的理论计算结果；

相量法（相量变换）的好处是：将对时域电路的分析映射到频域里，这样做的好处是将描述时域电路的微分方程转化为频域内的代数方程，从而大大简化对电路分析的复杂性。

借用网上的解释：如果说自然数是来源于对数量的刻画，有理数是来源于对比列的刻画，无理数是来源于对长度的刻画，那么，复数就完全是人为制造。

我想说的是：正是因为电工技术的发展，证明了复数存在的价值。

如果将来学到经典控制理论（自动控制原理），使用拉普拉斯变换，可以将一个系统的时域中的高阶微分方程转化为复频域内的代数方程，从解方程来看，好处是大大的。

4.2 正弦量的相量表示

一、正弦量的表示方法

1.解析式：使用函数表达式 瞬时值用小写字母表示

2.图形表示：波形图

为了便于运算，通常使用相量表示法：

二、旋转矢量与正弦量

设定：

则：该旋转的有向线段每一瞬时在纵轴上的投影即表示相应时刻正弦量的瞬时值。

三、用相量表示正弦量

相量：表示正弦量的复数称为相量。

相量表示法：用模值等于正弦量的最大值（或有效值）、辐角等于正弦量的初相的复数对应地表示相应的正弦量。

最大值相量：模用最大值表示，即

有效值相量：模用有效值表示，即

相量图：把相量表示在复平面的图形。

需要强调一下几点：

① 相量与正弦量是对应关系（ 是一种映射 时域到频域的映射 ），而并不是相等关系。

② 只有正弦量才能用相量表示，非正弦量不能用相量表示。

③ 只有同频率的正弦量才能画在同一相量图上。

4.3 正弦交流电路中的理想电路元件

在正弦电流电路中，无源元件除电阻外，还有电感和电容。

4.3.1 电阻

一、线性电阻元件

电阻元件伏安关系：关联参考方向

二、正弦交流电路中的电阻：

电阻元件两端电压和电流同相位,大小是电流的R倍。波形及相量如下图所示：

欧姆定律的相量形式：

电阻元件的功率（瞬时功率、平均功率、有功功率）：

4.3.2 电感

一、线性电感元件：

电感元件：描述线圈通有电流时产生磁场、储存磁场能量的性质。

磁链单位：韦伯（Wb） 电流单位：安培（A） 电感单位：亨利（H）

二、电感元件的电压电流关系：

关联参考方向

根据电磁感应定律，感应电动势的量值等于磁链的变化率，即

由感应电动势得电压，当取电压参考方向与磁链参考方向符合右螺旋法则时，即 u、e 和i参考方向均相同，如图所示，则有

电感两端的电压与通过该电感中电流的变化率成正比。

三、电感元件的磁场能量：

在电压和电流关联参考方向下，电感元件吸收的瞬时功率为

当电流由0增大到i时，电感元件储存的磁场能量为

能量单位：焦耳（J） 电流单位：安培（A） 电感单位：亨利（H）

总结：

• 电感元件是一种储能元件，同时又是一种无源元件。
• 磁场能量只与最终电流值有关，与电流建立过程无关。
• 电流i 绝对值增加时，电感元件吸收电能转换为磁场能量；i 绝对值减小时，电感元件释放磁场能量，转换为电能。

四、正弦交流电路中的电感元件

设电感元件的电流为：

感抗的大小，与频率有关，频率越高，感抗越大；对于直流电路，频率为零，所以感抗也为零（视为短路）。所以我们说，电感元件具有通直阻交的作用。

则在正弦交流电路中，电感元件伏安关系的相量形式可以表示为：

纯电感不消耗能量，只和电源进行能量交换。电感元件是储能元件。

在这里，我们做如下定义：

无功功率Q：瞬时功率的最大值，即

无功功率单位：乏（var）无功功率反映了电感元件与外部电路交换能量的规模。

4.3.3 电容

一、线性电容元件：

电容器：将两块金属极板用绝缘介质隔开，就形成了一个电容器。

电容元件：描述在这种两金属极板间的介质中所产生的电场和储存电场能量的性质。

电容定义为：

线性电容：C为常数；非线性电容：C不为常数

电荷单位为库仑（C） 电压单位为伏特（V） 电容单位为法拉（F）

二、电容元件的串、并联

串联：设n个电容相串联，则总电容

并联：设n个电容相并联，则总电容

三、电容元件的电压电流关系：

当电容器两个极板之间电压发生变化时，极板上电荷也会随着改变，于是连接电容器的电路中就会出现电流。按照如图参考方向下，电流为

u、i关联参考方向

通过电容的电流与电容两极板间电压的变化率成正比。

说明：当电容元件的电压、电流取非关联参考方向时，上式右边加负号。

四、电感元件的电场能量：

在电压和电流关联参考方向下，电容元件吸收的瞬时功率为

当电压由0增大时，电容元件储存的电场能量为

能量单位：焦耳（J） 电压单位：伏特（V）电容单位：法拉（F）

总结：

• 电容元件是一种储能元件，同时又是一种无源元件。
• 电场能量只与最终电压值有关，与电压的建立过程无关。
• 电压u绝对值增加时，电容元件吸收电能；u 绝对值减小时，电容元件释放电场能量。

五、正弦交流电路中的电容元件

设电容元件的电压为：

则电容元件的电流为：

令：

容抗的大小，与频率有关，频率越高，容抗越小；对于直流电路，频率为零，所以容抗为无穷大（视为开路）。所以我们说，电感元件具有隔直通交的作用。

则在正弦交流电路中，电容元件伏安关系的相量形式可以表示为：

六、电容元件的功率：假设

1.瞬时功率

2.平均功率

结论：纯电容不消耗能量，只和电源进行能量交换。电容元件是储能元件。

在这里，我们做如下定义：

无功功率Q：瞬时功率的最大值，即

无功功率单位：乏（var） 无功功率反映了电容元件与外部电路交换能量的规模。

4.4 耦合电感元件

一、耦合线圈的自感和互感

在上图中：

互感的定义：根据电磁场理论，只要磁场的介质是静止的，可以证明：

所以可统一用 M 表示，称为互感。其单位是：亨利 H 。互感在大小上反映了一个线圈在另一个线圈产生磁链的能力。

耦合系数K：表征耦合线圈的紧密程度，其定义为：

式中 L1 和 L2 为两个线圈的自感，M为互感。

耦合系数k 的范围为：0≤k≤1 。大小与L1和L2两个线圈的结构、相互位置以及磁介质有关。如果两个线圈紧密绕在一起，则 k 值可能接近于1。如果两线圈相隔很远，或者它们的轴线相互垂直，则 k 值很小，甚至可能接近于零。

二、耦合线圈的总磁链

取总磁链与自感磁链具有相同的参考方向：互感磁链有时为正，有时为负

显然，总磁链由自感磁链和互感磁链两部分构成，其中互感磁链有时为正，有时为负，同过同名端来表示互感磁链的正负。

同名端的概念：当电流 i1 和 i2 在耦合线圈中产生的磁场方向相同时，电流 i1 和 i2 流入（或流出）的两个端钮称为同名端，用一对符号“﹡”，“˙”，“△”表示。

解释：如果两个线圈的电流都由同名端流入，则每个线圈的总磁链为自感磁链与互感磁链相加；如果两个线圈的电流由异名端流入，则每个线圈的总磁链为自感磁链与互感磁链相减。

三、耦合线圈的感应电压

设每个线圈的电压、电流、磁链为关联的参考方向：

每个线圈的总电压均由自感电压和互感电压两部分组成。如果取自感电压，互感电压与线圈总电压参考方向相同，则自感电压总是正的，互感电压可能为正，也可能为负。

当电流的参考方向与另一个线圈电压的参考方向对同名端相关联时，互感电压为正；当电流的参考方向与另一个线圈电压的参考方向对同名端非关联时，互感电压为负。

四、耦合电感元件

由实际耦合线圈抽象出来的理想化的电路模型，由L1、L2和 M 三个参数表征，是一种线性二端口元件。

耦合电感元件的相量模型：正弦交流电路中的耦合电感元件

五、耦合电感的串联

1、同向串联：即把两线圈的异名端连接在一起。

两线圈同向串联时的等效电感

2、反向串联：即把两线圈的同名端连接在一起。

两线圈反向串联时的等效电感

两个线圈同向串联时，等效电感增大；反向串联时，等效电感减小。但其耦合等效电感 L 不可能为负（因为有 ）。所以：

六、耦合电感的并联

1、同名端并联

由基尔霍夫定律KCL和KCL：

可以得到：

可以推导出去耦等效电路如图，注意去耦等效之后原电路中的结点A的对应点为图中的A点而非A＇点。

耦合电感按同名端并联的等效阻抗为：

式中 L 为等效电感：

2、异名端并联

同理可得，去耦等效电路：

则耦合电感按异名端并联的等效电感为：

七、去耦

当耦合电感的两个线圈不是并联，但它们有一个端钮相连接，即有一个公共端的时候，仍然可以使用去耦法，可以把有耦合电感的电路化为去耦后的等效电路。

根据基尔霍夫两定律列写方程：

可以得到：

所以，去耦等效电路为：

如图(a)所示，耦合线圈同名端的位置发生改变，同理可推导其去耦等效电路，如图(b)所示：

含耦合电感电路的一般计算方法：

在计算含有耦合电感的正弦电流电路时，采用相量表示电压、电流，前面介绍的相量法仍然适用。但由于某些支路具有耦合电感，这些支路的电压不仅与本支路的电流有关，同时还与那些与之有耦合关系的支路电流有关，因而象阻抗的串并联公式、节电压法等不便直接应用。

而以电流为未知量的支路电流法、网孔电流法则可以直接应用，因为互感电压可以直接计入KVL方程中。