

贝叶斯深度学习介绍
描述
1 Introduction
基于深度学习的人工智能模型往往精于 “感知” 的任务,然而光有感知是不够的,“推理” 是更高阶人工智能的重要组成部分。比方说医生诊断,除了需要通过图像和音频等感知病人的症状,还应该能够推断症状与表征的关系,推断各种病症的概率,也就是说,需要有“thinking”的这种能力。具体而言就是识别条件依赖关系、因果推断、逻辑推理、处理不确定性等。
概率图模型(PGM)能够很好处理概率性推理问题,然而PGM的弊端在于难以应付大规模高维数据,比如图像,文本等。因此,这篇文章尝试将二者结合,融合到DBL的框架之中。
比如说在电影推荐系统中,深度学习适于处理高维数据,比如影评(文本)或者海报(图像);而概率图模型适于对条件依赖关系建模,比如观众和电影之间的网络关系。
从uncertainty的角度考虑,BDL适合于去处理这样的复杂任务。复杂任务的参数不确定性一般有如下几种:(1)神经网络的参数不确定性;(2)与任务相关的参数不确定性;(3)perception部分和task-specific部分信息传递的不确定性。通过将未知参数用概率分布而不是点估计的方式表示,能够很方便地将这三种uncertainty统一起来处理(这就是BDL框架想要做的事情)。
另外BDL还有 “隐式的”正则化作用,在数据缺少的时候能够避免过拟合。通常BDL由两部分组成:perception模块和task-specific模块。前者可以通过 权值衰减或者dropout正则化 (这些方法拥有贝叶斯解释),后者由于可以 加入先验 ,在数据缺少时也能较好地进行建模。
当然,BDL在实际应用中也存在着挑战,比如时间复杂性的问题,以及两个模块间信息传递的有效性。
2 Deep Learning
这一章主要介绍经典的深度学习方法,这里不用过多的篇幅去叙述,文章中提到的方法包括MLP、AutoEncoder、CNN、RNN等。
2.2 AutoEncoders
这一部分提一下自编码器。这是一种能将输入编码为更紧凑表示的神经网络,同时能够将这种紧凑表示进行重建。这方面的资料也很多,这里主要说明一下AE的变种——SDAE(Stacked Denoising AutoEncoders)
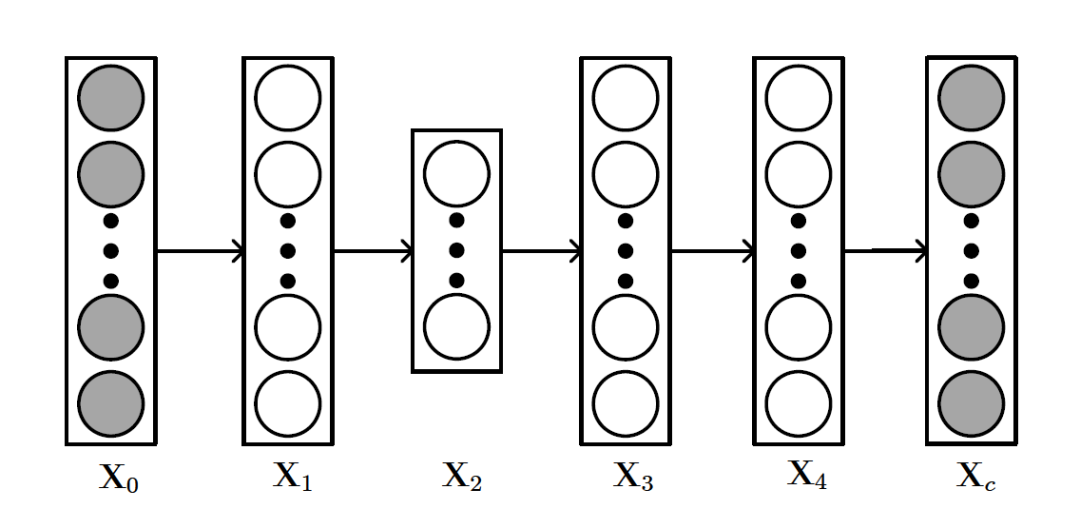
SDAE的结构如上图所示,和AE不同的是, 可以看做输入数据
可以看做输入数据 加入噪声或者做了一些随机处理后的结果(比如可以把
加入噪声或者做了一些随机处理后的结果(比如可以把 中的数据随机选30%变为零)。所以SDAE做的就是试图把处理过的corrupted data恢复成clean data。SDAE可以转化为如下优化问题:
中的数据随机选30%变为零)。所以SDAE做的就是试图把处理过的corrupted data恢复成clean data。SDAE可以转化为如下优化问题:
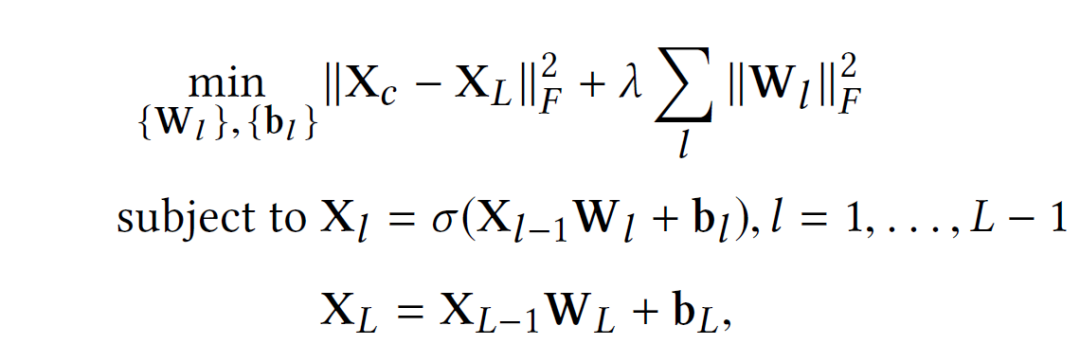
3 Probabilistic Graphical Model
这一章主要介绍概率图模型,也是为后面的内容做知识铺垫的,概率图模型的相关资料有不少,因此这里不过多叙述。文章主要介绍的是有向贝叶斯网(Bayesian Networks),如LDA等模型。LDA可以拓展出更多的topic model,如推荐系统中的协同话题回归(CTR)。
4 Bayesian Deep Learning
在这个部分,作者列举了一些BDL模型在推荐、控制等领域的应用,我们可以看到,众多当前实用的模型都可以统一到BDL这个大框架之下:
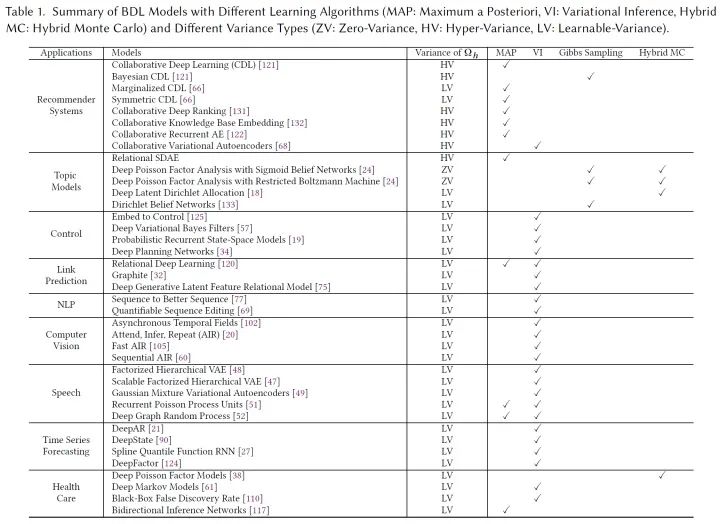
4.1 A Brief History of Bayesian Neural Networks and Bayesian Deep Learning
和BDL很相似的是BNN(Bayesian neural networks),这是一个相当古老的课题,然而BNN只是本文BDL框架下的一个子集——BNN相当于只有perception部分的BDL。
4.2 General Framework
如下图是文章提出的基本框架,红色部分是 感知模块 ,蓝色部分是 任务模块 。红色部分通常使用各种概率式的神经网络模型,而蓝色部分可以是贝叶斯网络,DBN,甚至是随机过程,这些模型会以概率图的形式表示出来。
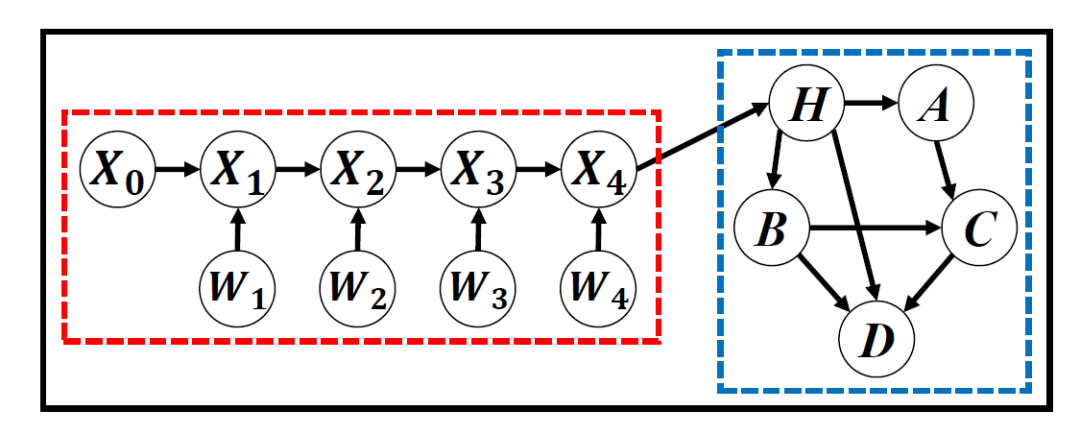
在这个基本框架中往往有三种变量:perception variables  (图中的X,W), hinge variables
(图中的X,W), hinge variables  (图中的H)和task variables
(图中的H)和task variables  (图中的A,B,C)。通常来说,红色模块和hinge variables之间的连接是独立的。因此,对于能归纳到BDL框架下的模型,我们都可以找到这样的结构——两个模块,三种变量。
(图中的A,B,C)。通常来说,红色模块和hinge variables之间的连接是独立的。因此,对于能归纳到BDL框架下的模型,我们都可以找到这样的结构——两个模块,三种变量。
BDL可以对红蓝两个部分之间信息交换的uncertainty进行建模,这个问题等价研究 的uncertainty(在公式中的体现就是条件方差)。方差的不同假设有:Zero-Variance(ZV,没有不确定性,方差为零),Hyper-Variance(HV,方差大小由超参数决定),Learnable Variance(LV,使用可学习参数表示)。显然,灵活性上有LV>HV>ZV。
的uncertainty(在公式中的体现就是条件方差)。方差的不同假设有:Zero-Variance(ZV,没有不确定性,方差为零),Hyper-Variance(HV,方差大小由超参数决定),Learnable Variance(LV,使用可学习参数表示)。显然,灵活性上有LV>HV>ZV。
4.3 Perception Component
通常来说,这一部分应该采用BNN等模型,当然我们可以使用一些更加灵活的模型,比如RBM,VAE,以及近来比较火的GAN等。文章提到了以下几个例子:
Restricted Boltzman Machine :RBM是一种特殊的BNN,主要特点有:(1)训练时不需要反向传播的过程;(2)隐神经元是binary的。RBM的具体结构如下:
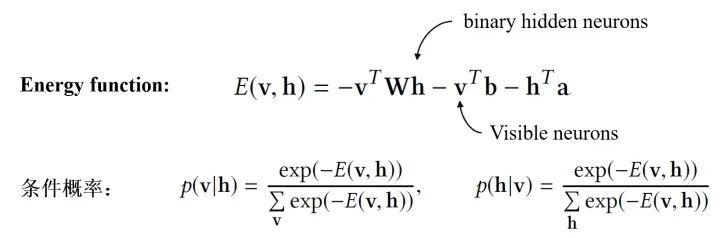
RBM通过Contrastive Divergence进行训练(而不是反向传播),训练结束后通过边缘化其他neurons就能求出 和
和 。
。
Probabilistic Generalized SDAE: 我们将2.2提到的SDAE加以改进,如果假设clear input  和corrupted input
和corrupted input  都是可以观察的 ,便可以定义如下的Probabilistic SDAE:
都是可以观察的 ,便可以定义如下的Probabilistic SDAE:

Variational Autoencoders :VAE的基本想法就是通过学习参数最大化ELBO,VAE也有诸多变种,比如IWAE(Importance weighted Autoencoders),Variational RNN等。
Natural-Parameter Networks :与确定性输入的vanilla NN不同,NPN将一个分布作为输入(和VAE只有中间层的output是分布不同)。当然除了高斯分布,其他指数族也可也当做NPN的输入,如Gamma、泊松等。
4.4 Task-Specific Component
这一个模块的主要目的是将概率先验融合进BDL模型中(很自然的我们可以用PGM来表示),这个模块可以是Bayesian Network,双向推断网络,甚至是随机过程。
Bayesian Networks :贝叶斯网是最常见的task-specific component。除了LDA,另一个例子是PMF(Probabilistic Matrix Factorization),原理是使用BN去对users,items和评分的条件依赖性建模。以下是PMF假设的生成过程:

Bidirectional Inference Networks :Deep Bayesian Network不止关注“浅相关”和线性结构,还会关注随机变量的非线性相关和模型的非线性结构。BIN是其中的一个例子。
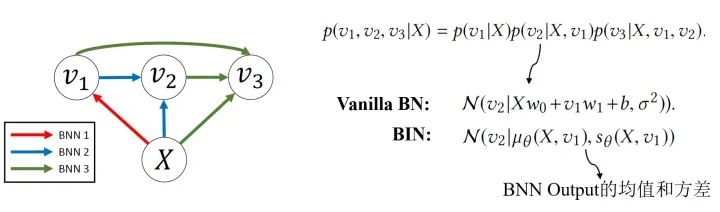
Stochastic Processes :随机过程也可以作为Task-component,比如说用维纳过程模拟离散布朗运动,用泊松过程模拟处理语音识别的任务等。随机过程可以被看做一种动态贝叶斯网(DBN)。
5 Concerte BDL Models and Applications
上一章讨论完构成BDL的基本模型结构,我们自然希望能够把这一套大一统的框架运用在一些实际的问题上。因此,这一章主要讨论了BDL的各种应用场景,包括推荐系统,控制问题等。在这里我们默认任务模块使用vanilla Bayesian networks作为这个部分的模型。
5.1 Supervised Bayesian Deep Learning for Recommender Systems
Collaborative Deep Learning 。文章在这个部分提出Collaborative Deep Learning(CDL)来处理推荐系统的问题,这种方法连接了content information(一般使用深度学习方法处理)和rating matrix(一般使用协同过滤)。
使用4.3.2提到的Probabilistic SDAE,CDL模型的生成过程如下:

为了效率,我们可以设置趋向正无穷,这个时候,CDL的图模型就可以用下图来表示了:
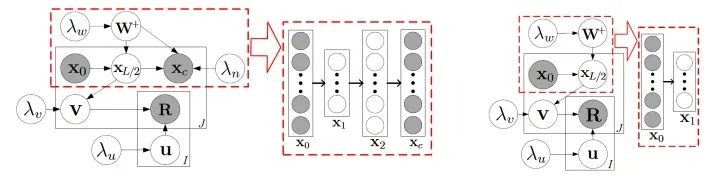
红色虚线框中的就是SDAE(图上是L=2的情况),右边是degenerated CDL,我们可以看到,degenerated CDL只有SDAE的encoder部分。根据我们之前定义过的, 就是hinge variable,而
就是hinge variable,而 是task variables,其他的是perception variables。
是task variables,其他的是perception variables。
那么我们应该如何训练这个模型呢?直观来看,由于现在 所有参数都被我们当做随机变量 ,我们可以使用纯贝叶斯方法,比如VI或MCMC,然而这样计算量往往是巨大的,因此,我们使用一个EM-style的算法去获得MAP估计。先定义需要优化的目标,我们希望最大化后验概率,可以等价为最大化给定 的joint log-likelihood。
的joint log-likelihood。
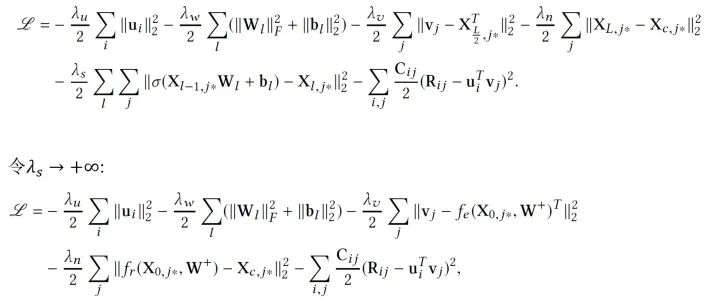
注意,当 趋向无穷时,训练CDL的概率图模型就退化为了训练下图的神经网络模型:两个网络有相同的加了噪音的输入,而输出是不同的。
趋向无穷时,训练CDL的概率图模型就退化为了训练下图的神经网络模型:两个网络有相同的加了噪音的输入,而输出是不同的。
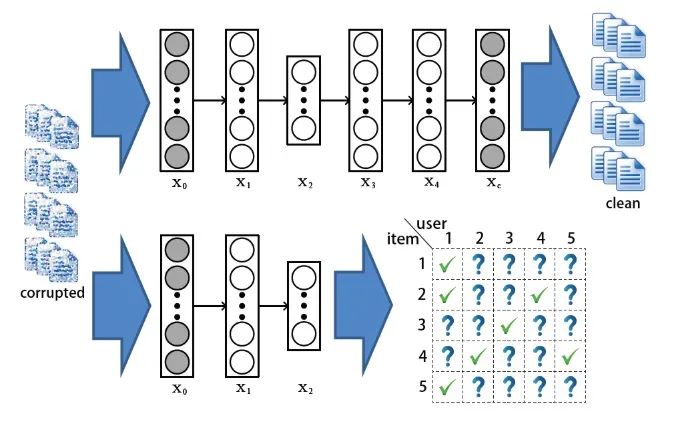
有了优化的目标,参数该如何去更新呢?和巧妙的EM算法的思路类似,我们通过迭代的方法去逐步找到一个局部最优解:
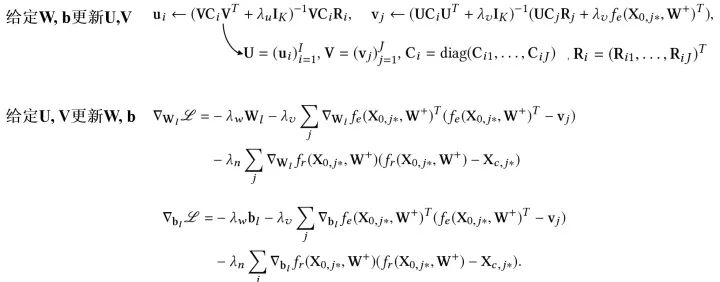
当我们估计好参数,预测新的评分就容易了,我们只需要求期望即可,也就是根据如下公式计算:
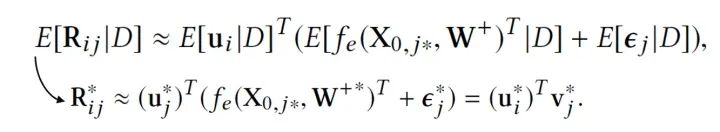
Bayesian Collaborative Deep Learning :除了这种模型,我们可以对上面提到的CDL进行另外一种扩展。这里我们不用MAP估计,而是sampling-based算法。主要过程如下:

当 趋向正无穷并使用adaptive rejection Metropolis sampling时,对
趋向正无穷并使用adaptive rejection Metropolis sampling时,对 采样就相当于BP的贝叶斯泛化版本。
采样就相当于BP的贝叶斯泛化版本。
Marginalized Collaborative Deep Learning :在SDAE的训练中,不同训练的epoch使用不同的corrupted input,因此训练过程中需要遍历所有的epochs,Marginalized SDAE做出了改进:通过边缘化corrupted input直接得到闭式解。
Collaborative Deep Ranking :除了关注精确的评分,我们也可以直接关注items的排名,比如CDR算法:

这个时候我们需要优化的log-likelihood就会成为:
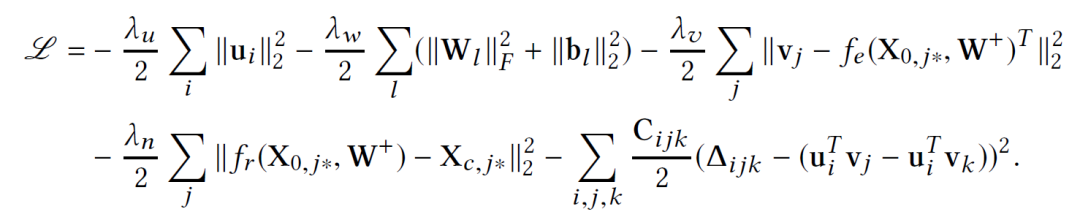
Collaborative Variational Autoencoders :另外,我们可以将感知模块的Probabilistic SDAE换成VAE,则生成过程如下:

总之,推荐系统问题往往涉及高维数据(文本、图像)处理以及条件关系推断(用户物品关系等),CDL这类模型使用BDL的框架,能发挥很重要的作用。当然其他监督学习的任务也可以参考推荐系统的应用使用CDL的方法。
5.2 Unsupervised Bayesian Deep Learning for Topic Models
这一小节过渡到非监督问题中,在这类问题中我们不再追求 “match” 我们的目标,而更多是 “describe” 我们的研究对象。
Relational Stacked Denoising Autoencoders as Topic Models (RSDAE) :在RSDAE中我们希望能在关系图的限制下学到一组topics(或者叫潜因子)。RSDAE能“原生地”集成潜在因素的层次结构和可用的关系信息。其图模型的形式和生成过程如下:
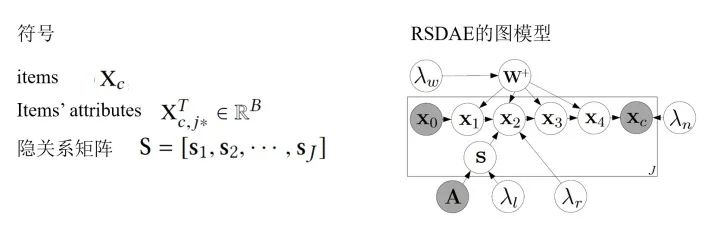

同样的,我们最大化后验概率,也就是最大化各种参数的joint log-likelihood:
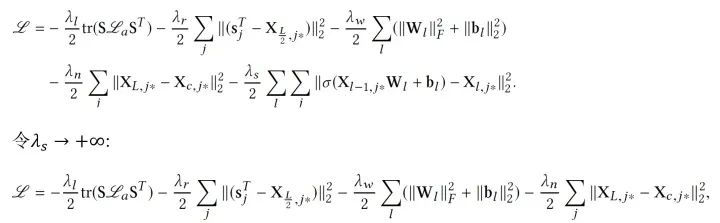
训练的时候我们依然使用EM-style的算法去找MAP估计,并求得一个局部最优解(当然也可以使用一些带skip的方法尝试跳出局部最优),具体如下:

Deep Poisson Factor Analysis with Sigmoid Belief Networks :泊松过程适合对于非负计数相关的过程建模,考虑到这个特性,我们可以尝试把Poisson factor analysis(PFA)用于非负矩阵分解。这里我们以文本中的topic问题作为例子,通过取不同的先验我们可以有多种不同的模型。
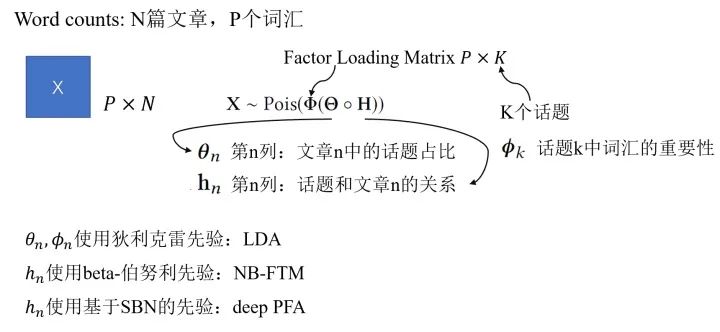
比如说,我们可以通过采用基于sigmoid belief networks(SBN)的深度先验,构成DeepPFA模型。DeepPFA的生成过程具体如下:

这个模型训练的方式是用Bayesian Conditional Density Filtering(BCDF),这是MCMC的一种online版本;也可以使用Stochastic Gradient Thermostats(SGT),属于hybrid Monto Carlo类的采样方法。
Deep Poisson Factor Analysis with Restricted Boltzmann Machine :我们也可以将DeepPFA中的SBN换成RBM模型达到相似的效果。
可以看到,在基于BDL的话题模型中, 感知模块用于推断文本的topic hierarchy,而任务模块用于对词汇与话题的生产过程,词汇-话题关系,文本内在关系建模 。
5.3 Bayesian Deep Representation Learning for Control
前面两小节主要谈论BDL在监督学习与无监督学习的应用,这一节主要关注另外一个领域:representation learning。用控制问题为例。
Stochastic Optimal Control :在这一节,我们考虑一个未知动态系统的随机最优控制问题,在BDL的框架下解决的具体过程如下:

BDL-Based Representation Learning for Control :为了能够优化上述问题,有三个关键的部分,具体如下:
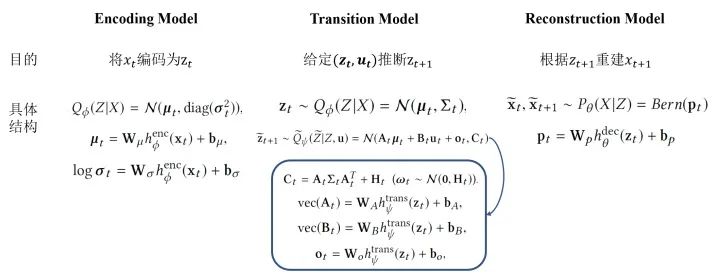
Learning Using Stochastic Gradient Variational Bayes :该模型的损失函数是如下这种形式:
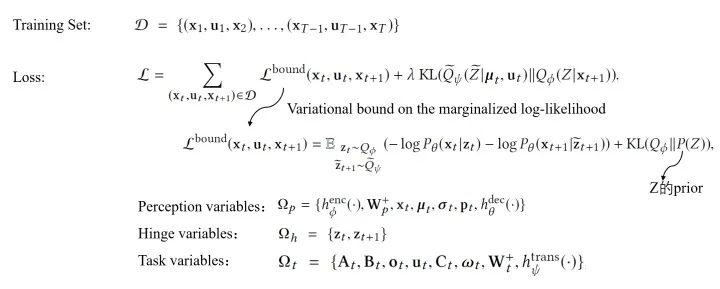
在控制的问题中,我们通常希望能够从原始输入中获取语义信息,并在系统状态空间中保持局部线性。而BDL的框架正好适用这一点,两个组件分别能完成不同的工作:感知模块可以捕获 live video,而任务模块可以推断动态系统的状态。
5.4 Bayesian Deep Learning for Other Applications
除了上面提到的,BDL还有其他诸多运用场景:链路预测、自然语言处理、计算机视觉、语音、时间序列预测等。比如,在链路预测中,可以将GCN作为感知模块,将stochastic blockmodel作为任务处理模块等。
6 Conclusion and Future Research
现实中很多任务都会涉及两个方面:感知高维数据(图像、信号等)和随机变量的概率推断。贝叶斯深度学习(BDL)正是应对这种问题的方案: 结合了神经网络( NN )和概率图模型(PGM)的长处 。而广泛的应用使得BDL能够成为非常有价值的研究对象,目前这类模型仍然有着众多可以挖掘的地方。
-
机器学习的朴素贝叶斯讲解2019-05-15 1739
-
六大步骤学习贝叶斯算法2019-07-16 2238
-
贝叶斯算法(bayesian)介绍2011-06-01 1285
-
机器学习之朴素贝叶斯应用教程2017-11-25 1530
-
机器学习之朴素贝叶斯2018-05-29 1123
全部0条评论

快来发表一下你的评论吧 !

