

支路电流法的电路分析
描述
在进行电路分析时,常常会遇到一些设计复杂的电路,这时就是一个头两个大,手上的欧姆定律好像有点不够用了。
对于不能简单用串联和并联进行简化的电路回路,常常就是比较难分析的那一类,这一类电路也叫复杂电路。碰到这类电路,就需要结合实际根据电路的结构特点来寻找和分析计算的简便方法。
比如说可以试试支路电流法,它可以说是计算复杂电路的最基本方法。
在分析上,它先是想象成各支路的电流都是未知的(未知量),然后根据基尔霍夫电流定律和基尔霍夫电压定律,根据未知量来列出方程,从而根据函数方程,来求解所需要的值是多少。
比如说下图中的电路,要如何进行支路电流法的使用来进行参数计算呢?
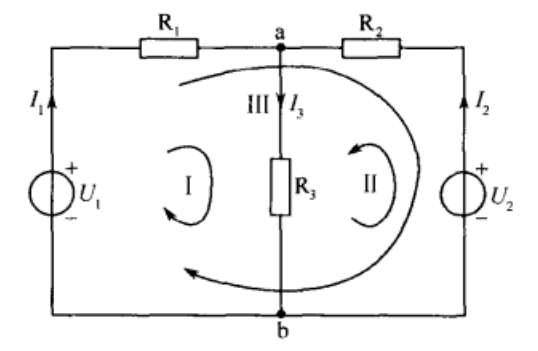
首先从图中可以看出,它是一个双电源电路,并且两个电源是并联的。此时先标出各个节点的字母位置标识(方面记录分析),画出各条支路上的电流方向。
本电路中有三条支路,2个节点(a和b),所以可以列出独立方程来进行求解。
所以根据基尔霍夫电流定律可以得到
结点a:I****1+I2-I3=0
结点b:I****3-I1-I2=0
然后电路也有回路(如图中画圈的箭头),通过基尔霍夫电压定律可以得到3个回路电压方程
回路1:U1-I1R1-I3R3=0
回路2:U2-I2R2-I3R3=0
回路3:U1-I1R1+I2R2-U2=0
通过以上的方式就可以列出多个方程来求解需要的未知量,就大体能求出相应的值啦。
最后求出来的值如果数值是正,则表示电流的实际方向和参考方向相同,如果数值是负,则表示电流的实际方向与参考方向相反。
那以上就是支路电流法求解复杂电路的方法了。
归结起来就是4步
(1)根据电路结构,确定电路的支路数和结点数,并标注好电流的参考方向和回路
(2)根据基尔霍夫电流定律,写出独立的电流方程式,其中与参考方向一致的电流为正,与参考方向相反的电流为负。
(3)根据基尔霍夫电压定律,写出独立的电压方程式,规定沿着绕行方向上,电压上升与下降分为为正和负
(4)最后根据第二步,第三步得到的公式来求解各参数
-
回路电流法和支路电流法的实质是什么2024-08-09 2713
-
支路电流法适用于非线性电路吗2024-08-08 1959
-
支路电流法是以什么为未知量2023-12-08 2841
-
支路电流法的解题步骤有哪些2021-09-28 6323
-
支路电流法计算步骤_支路电流法的适用条件2021-01-15 61948
-
支路电流法2009-07-27 9753
-
支路电流法说课稿2009-07-08 1540
-
电路的分析方法2009-07-07 2041
-
什么是支路电流法2008-08-16 4738
全部0条评论

快来发表一下你的评论吧 !

