与电源无关的偏置电流你真的懂了吗？

做模拟IC的，大部分都熟悉Razavi那本经典之作，书中有一小节介绍过一个“与电源无关的偏置电流（Current Bias）”。好了，问题来了，

请听题，以下这张图中，宽长比尺寸M3=M4, M2=K*M1 （K>1），请问哪个是正确的“与电源无关的偏置电流”，抑或是这两个都正确、实际IC中都可以用吗？

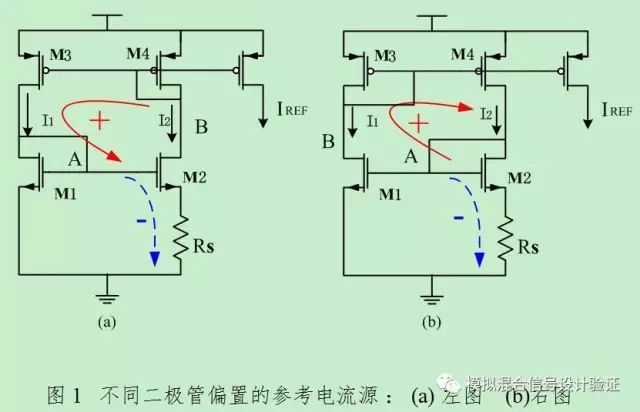
偏置电流？是的，一个IC系统，一般都需要有电流源来给其他模块提供参考电流。一个好的参考电流源，要环路稳定，也需要尽量减少其对电源电压、温度以及工艺的变化的影响。

表面上看这两个电路图都实现了Current Bias的功能。该电路中由两个M3和M4尺寸相等，构成电流镜结构，所以I1 =I2 。M2尺寸是M1的K倍，根据M1和M2的VGS之差(主要是有落在M2管源端电阻Rs上的压降造成的)可以得到输出电流的表达式：

若M1,M2管是工作在饱和区，则输出参考电流Iref以及M1的跨导分别为 ^[^ ^1^ ^]^ ：（拿个小本本，自己去推算了哦，这里就不写详细步骤了）

若M1,M2管是工作在亚阈值区，则由于亚阈值区的工作电流为：

其中，I0为单位饱和电流，VT = kT/q，ζ是亚阈值斜率因子。如果VDS >>VT ，那么exp(VGS /ζVT )可以忽略。因I1 =I2 ，所以输出参考电流Iref以及M1的跨导分别为：

虽然看着偏置电流值都一样，但是其他方面呢？正如上图红色箭头线所标志的一样，如果A点向上扰动的话，经过环路一整圈以后，还是向上扰动；也就是说这是一个正反馈环路。那么这个环路能稳定么？

以下通过两种方法来分析一下。

第一种稳定性分析方法是从整体环路增益角度来看两个电路。对于图1 (a)电路中的整体环路增益为(为计算方便，应从A点断开,信号向B点传输，即逆时针方向)：

而对于图1(b)电路中的整体反馈环路增益为(为计算方便，应从A点断开,信号向B点传输，即顺时针方向)：

根据奈奎斯特定律 ^[2]^ ：“如果一个系统在180°相移处，环路增益大于1，则这个放大器是不稳定的”；所以无论NMOS管是工作在饱和区，还是在亚阈值区，都有图1中(a)电路、也即传统经典电路是稳定的，而(b)则不是稳定的。

第二种稳定性分析方法是采用直观观察法；哈哈，终于等来了大家喜闻乐见的“直觉”感。由于M3, M4是电流镜，所以下面的NMOS管和电阻应该在相同的栅电平下保证能提供相同的电流。M1管的跨导为g m ，而M2和电阻的等效跨导为：

由于M2的等效跨导较小(其实也可以从负反馈角度考虑，负反馈检测电流，反馈回电压，所以M2是跨导放大器，由于结成了负反馈，所以肯定跨导要减小)，所以为了保证左右支路电流始终相等，还是从A点断开，A点左边的电压变化比A点右边的小即可满足。（挺住哈，别被饶晕过去哈！）

而图 1 (a)中正反馈的方向是逆时针的，所以M2处大的电压波动，到了M1的栅端反而变小了，所以正反馈减弱，系统稳定。

而图1 (b)中正反馈的方向是顺时针的，M1处有电压波动时，通过正反馈环，到M2处需要更大的电压波动才能保证相同的电流，即M1处的电压被放大了，所以系统不稳定。

随着集成电路工艺的不断先进，最小线宽的不断减小，其也同时要求最低工作电压在不断减小；在低压环境中，电源上的微小噪声就显得不再“微小”了，其就更是可以影响整个系统环境。随着数模混合电路和射频电路的不断发展，以及其单片片上集成(SOC)技术的发展，电源噪声对于一些敏感电路(对电源变化和噪声敏感的电路)而言，非常容易影响其的性能，进而影响整个系统的性能。

例如，手机或者蓝牙中一般含有的射频RF电路，包括LNA(低噪声放大器)、混频器mixer、锁相环PLL、压控振荡器VCO等，如果有电源噪声，则会增大VCO的相位噪声，而且会进入接收或者发送放大器，从而对系统正常工作造成非常大的影响，不仅是手机系统的音频质量会下降，而且会造成多媒体手机拍摄的图像中有可视的干扰，所以必须对电源噪声进行处理之后才能给敏感模块使用。

咱们的电流偏置，也更是要考虑低电压应用下，对电源的抑制能力(Power Supply Rejection)啊！

以上分析的经典电路，其电源抑制能力也较一般。原因在于虽然说M3,M4构成了电流镜，其栅源电压均相等，但是由于两者的漏端和电源VDD的相关性不同：M3的漏端随着VDD的变化而变化，M4的漏端和VDD没有直接关系；所以两者电流拷贝存在误差。

可以采用共源共栅结构来改善该问题，如下图图2所示。可以计算该电路的环路增益，其实和传统的参考电流源一样，但是通过共源共栅结构，使得电流镜拷贝准确度提高了大约gmro倍，使得电流较准。

但是低压环境限制了共源共栅的应用。因为该结构的最小电源电压为IRs+Vthn+Vonn+|Vthp|+|Vonp|，很容易超过2 V。哎呀，飞升上神的路上又遇阻了：有没有再理想的一种电流源结构，能很好的解决了PSR的问题，同时又不需要特别高的电源电压呢？

答案当然是有了！下文介绍的三支路电流源 ^[3]^ 就能很好的解决PSR的问题，同时又不需要特别高的电源电压。

因为其将M3管的diode连接结构转至M5管，那么电源变化时对M3和M4的影响就小了。同时可以通过调整M5和M6，使Vg6=Vg2，即图中B点和C点电压相等，VB=VC，那么M3，M4管工作状态基本完全一样，基准电流的电源抑制特性得到加强。

该电路也有环路，一个是红色实线显示的正反馈，一个是蓝色虚线显示的负反馈。可以分别计算一下其环路增益：(这里不妨假设M1管和M6管相同，M2管尺寸依然是两者的K倍；M1, M6, M2均可以工作在饱和区或者亚阈值区。)

可以看出来同经典的Bias电路相同，三支路电流源也是负反馈大于正反馈，所以该系统是稳定的。

这个电路，还有改进的空间！！做IC嘛，谁不是天天在压成本、省面积？所谓的：卖的白菜价、操的白粉心；学的比互联网难、挣的比互联网少。改进，继续改：这里主要改进的是M6管的连接方式，其电流也流过了Rs电阻（见图4），所以所需要的Rs电阻可以明显减小，从而节约了芯片总面积 。同时为了减小系统功耗，需要尽量的降低各路电流，所以Bias产生电流较小。若M1, M2, M6管工作在饱和区，那么可能需要用倒比管，而倒比管模型的仿真精确度不如常规的管子；所以可以采用M1, M2, M6管工作在亚阈值区。

假设Ki表示Mi管相对于单位尺寸的倍数，可以根据M1管和M2管的栅电压VG相同列出等式，其中将M1，M2管的Vgs电压通过式(1-4)代入等式，而可以得到输出参考电流表达式为：

这个偏置电流和电源电压的相关性非常小，所以PSR比较好。