夯实基础之模拟运算放大器分享

介绍一下为什么我们需要运算放大器这样一种电路。

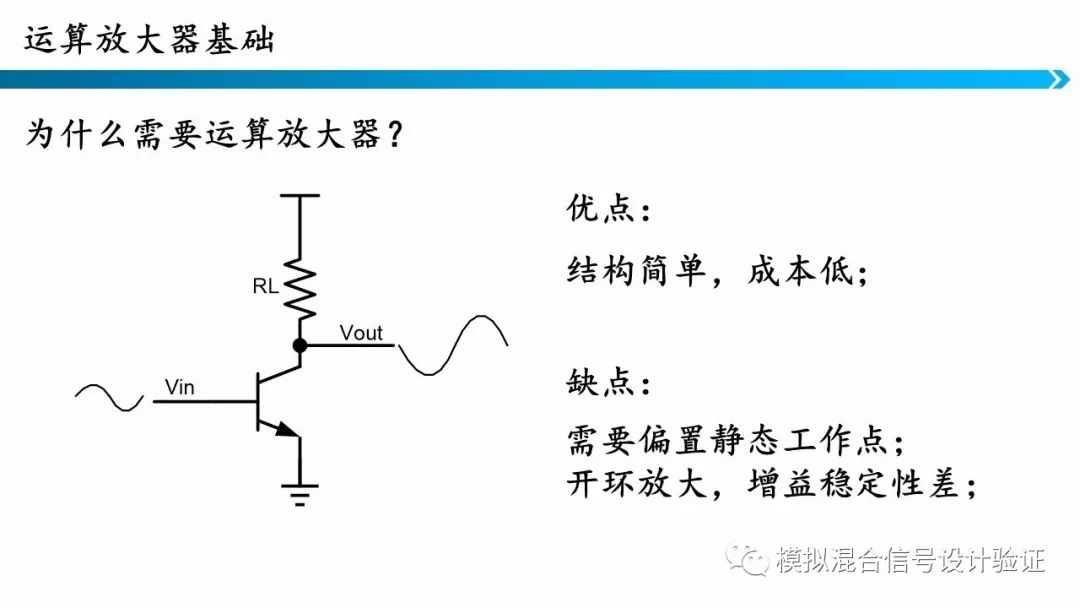
运算放大器出现之前，模拟放大器就已经存在了，它的结构如图所示，这个电路通过三极管实现反相放大，更早以前的放大电路是通过电子管构建的。这个电路的优点是结构简单，成本低。但是它也存在严重的缺点，首先是它需要一个静态工作点，而且每一个电路需要的工作点都有可能不相同，需要单独的调试。其次这个电路是开环放大的，所以电路的增益稳定性很差。

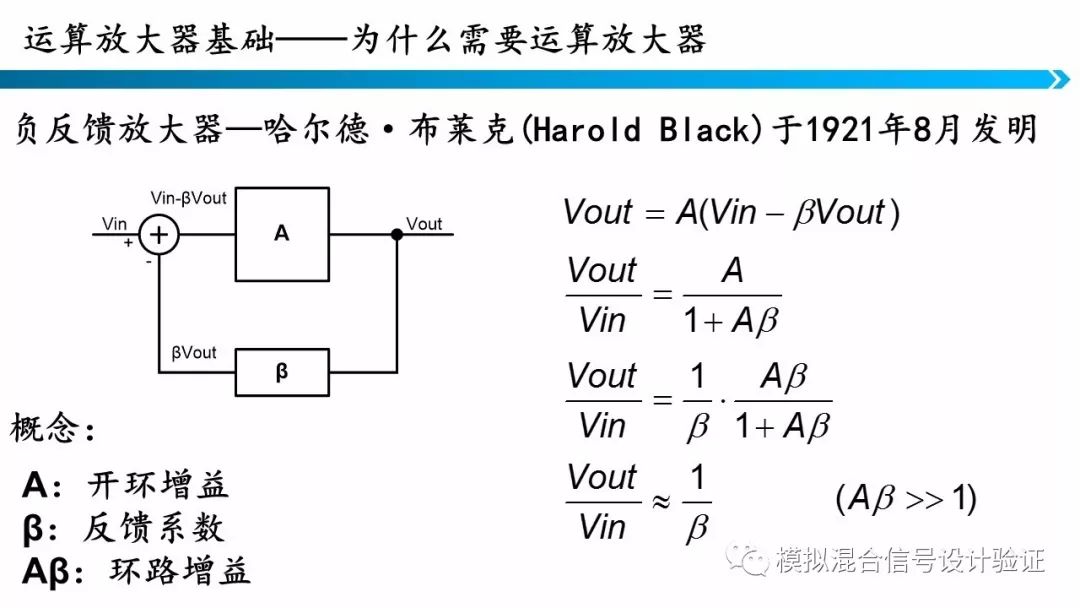
为了克服上面几个问题，布莱克在放大器中引入了负反馈，负反馈的具体推导如图，具体原理不再赘述。负反馈放大器中有三个非常重要的概念，首先是开环增益A，开环增益就是放大器的增益；其次是反馈系数β；最后是环路增益Aβ。环路增益在运算放大器中很重要，从图中的推导可以看出，在环路增益远大于1的条件下，系统闭环的增益只取决于反馈系数，避免了前向增益的影响，更详细的推导大家可以看教科书。在Aβ远大于1 这个条件下，我们可以看出，A必须取的很大，这个器件就是我们的运算放大器。β就代表我们的反馈网络。

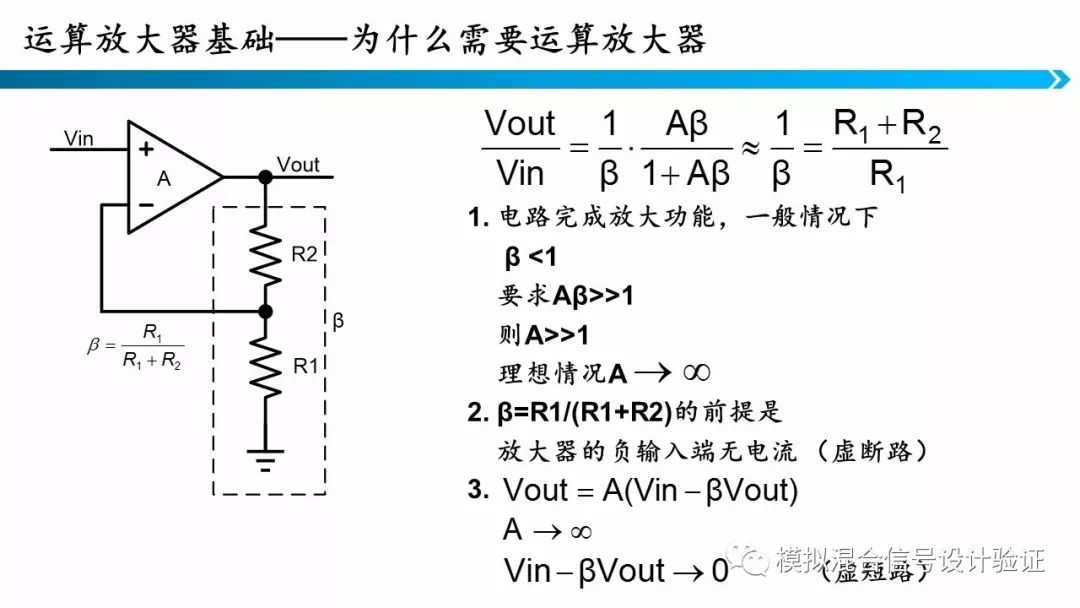
上一张是运算放大器的数学模型，这一张展示的就是实际运算放大器的一个例子。和上一张PPT相对应，运放提供了一个前馈增益，分压电阻提供了一个反馈网络。这里主要讲三点，第一，由于反馈系数β<1是恒成立的，为了保证Aβ远大于1 这个条件成立，就需要使A很大，对于理想放大器A可以视为无穷大。第二，对于电阻反馈网络，反馈系数写成R1和R2分压的形式，它的前提是放大器的负输入端应当是断路的。因为根据基尔霍夫电流定律，如果放大器负输入端有电流流入，反馈系数就不能简单写作分压的形式。这就是我们常说的“虚断路”。第三，从前向通路上看，输出电压可以写成前向增益A与误差(Vin-βVout)的乘积，在实际电路中，放大器的输出摆幅必定是有限的，而开环增益A是无穷大的，所以只能使放大器的正负输入端电压相等，这就是虚短路。

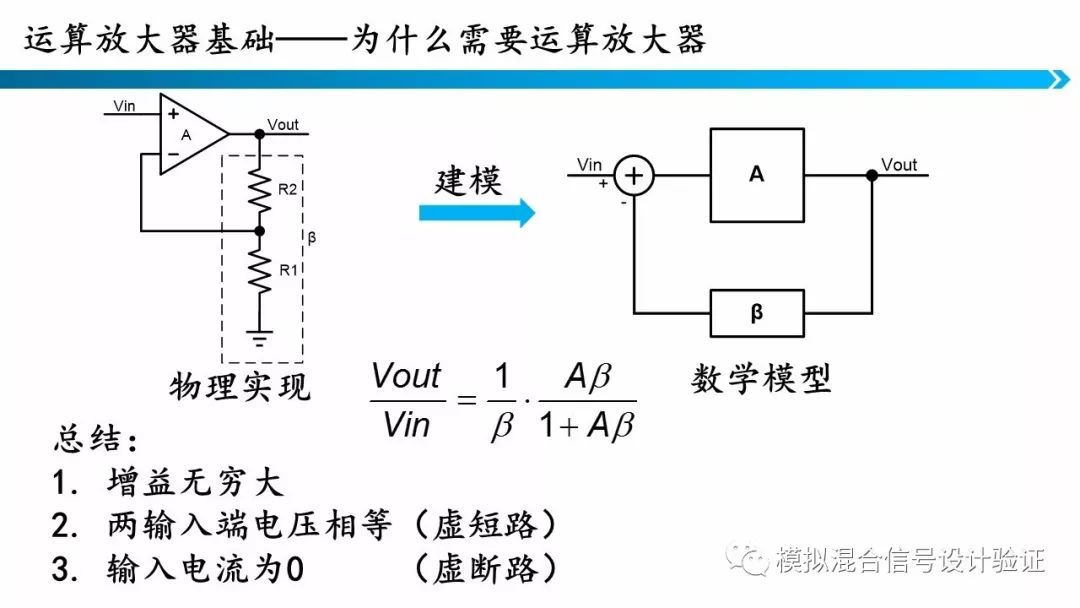
回到之前的问题，我们为什么会需要一个运算放大器呢？就是因为我们有这样的反馈系统，在这个反馈系统中，如果能够构建一个开环增益无穷大，同时输入端不需要电流的器件，就可以将这个器件放在反馈系统中，使反馈系统达到稳定。此时输出电压不依赖于前向增益，只依赖于电阻反馈网络，而电阻的比例是可以精确实现的。

运算放大器的设计目标就是这个理想的器件，但在实际中是很难达到的，实际放大器的设计往往是各种参数的折衷，提高了一个参数会牺牲另一个参数。

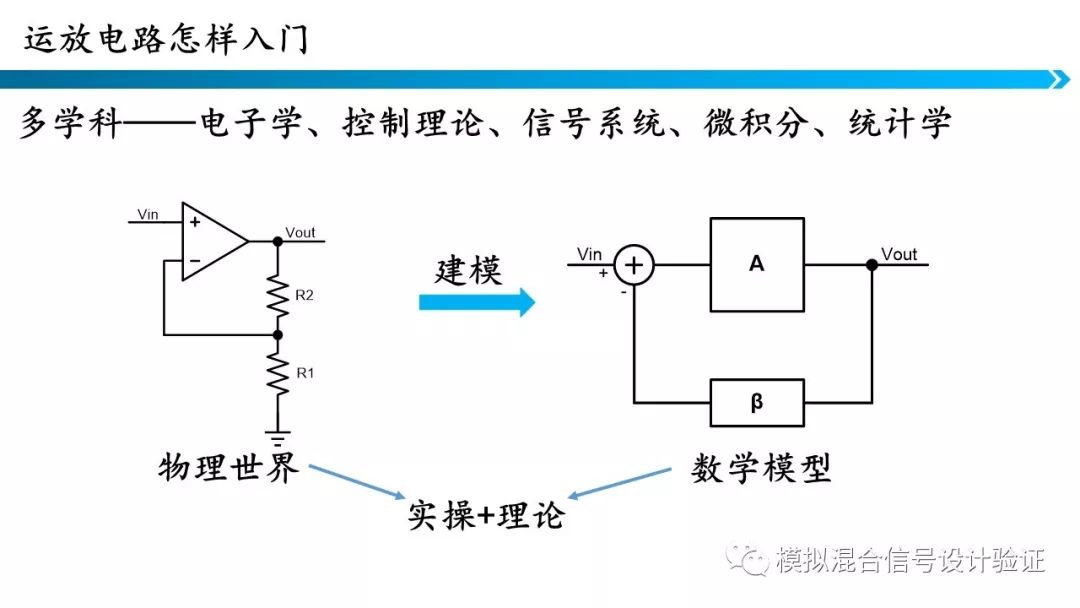
第二部分是关于运算放大器电路的分析，在分析运算放大器时需要哪些知识呢？实际上，模拟电路的确入门较难，需要多学科的交叉，包括电子学、控制理论、信号与系统、微积分等等。但是也不要因为这些就害怕学习模拟电路，因为模拟电路设计只是在某些时候会用到这些学科的基础知识，并不需要精通。

这一张ppt列举了很多做模拟电路需要了解的知识，其实这些知识在各自的学科中都很基础。打好基础会对我们设计模拟电路大有裨益。下面我们对刚刚列举的知识点作一个简单介绍。

1.能量守恒

能量守恒是电路系统必须满足的一个定律，实际上工作中很多人在分析电路时，用了很多复杂的分析方法，最后发现不满足能量守恒，这样就是明显的错误。其实能量守恒应用在电路中的最重要结论就是基尔霍夫电压定律。

2.电荷守恒

和能量守恒相对应的就是电荷守恒，在做一些和电容相关的分析时会经常用到。同样的，电荷守恒应用在电路中的最重要结论就是基尔霍夫电压定律。

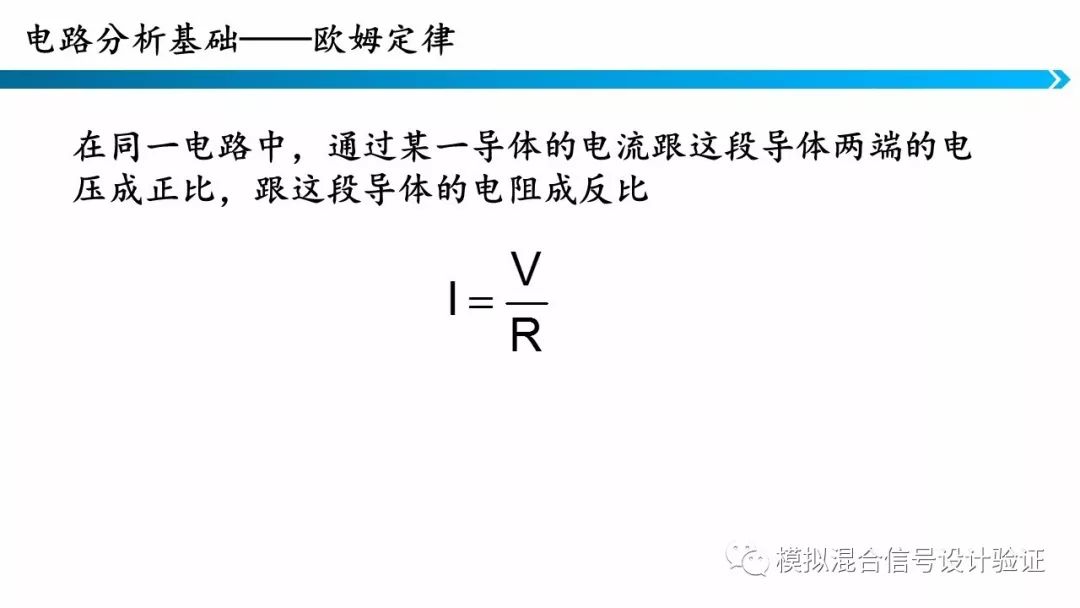
3.欧姆定律

欧姆定律描述了电阻器件两端口之间的电压电流关系。

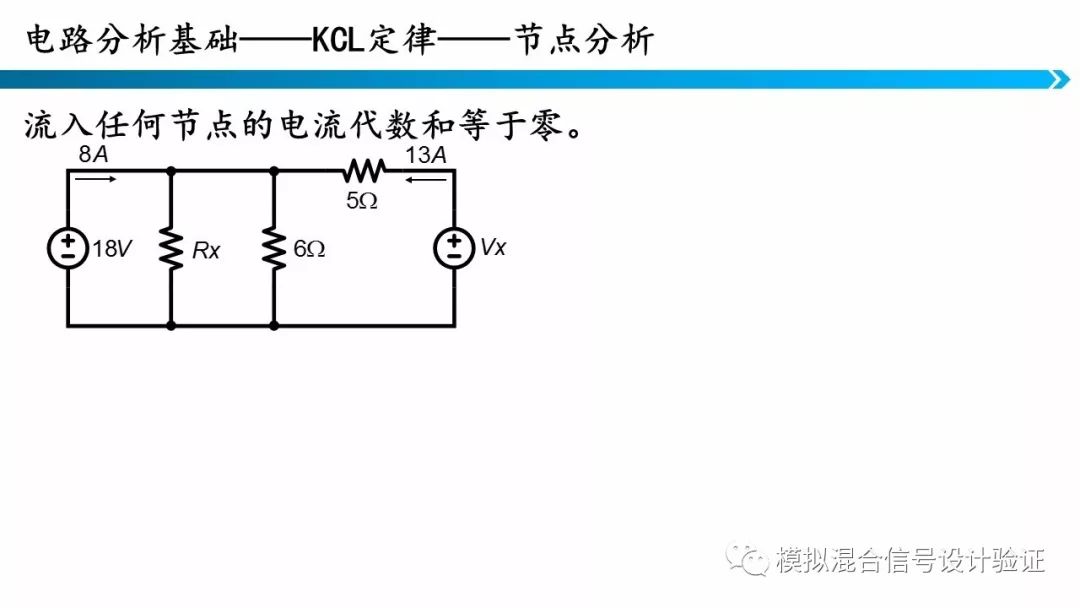
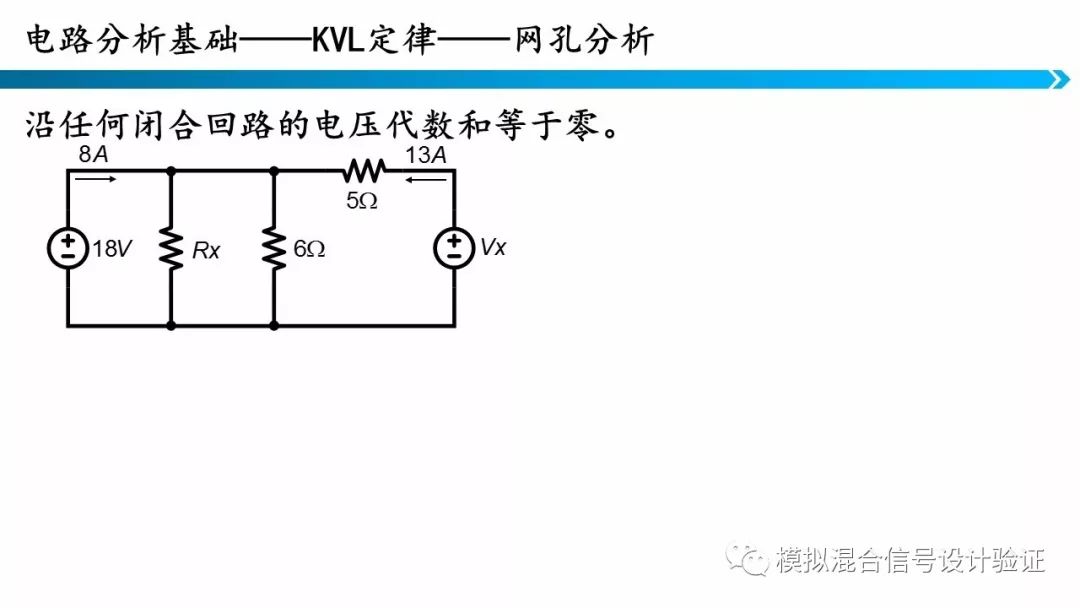
4.基尔霍夫电压定律与基尔霍夫电流定律

电路分析的基础方法就是基尔霍夫电压定律与基尔霍夫电流定律再加上欧姆定律列写电路方程并求解。当然了，当电路过于复杂时，利用这种方法求解电路会非常复杂，所以在电路分析中人们又引入了戴维南等效等工具来简化电路分析。

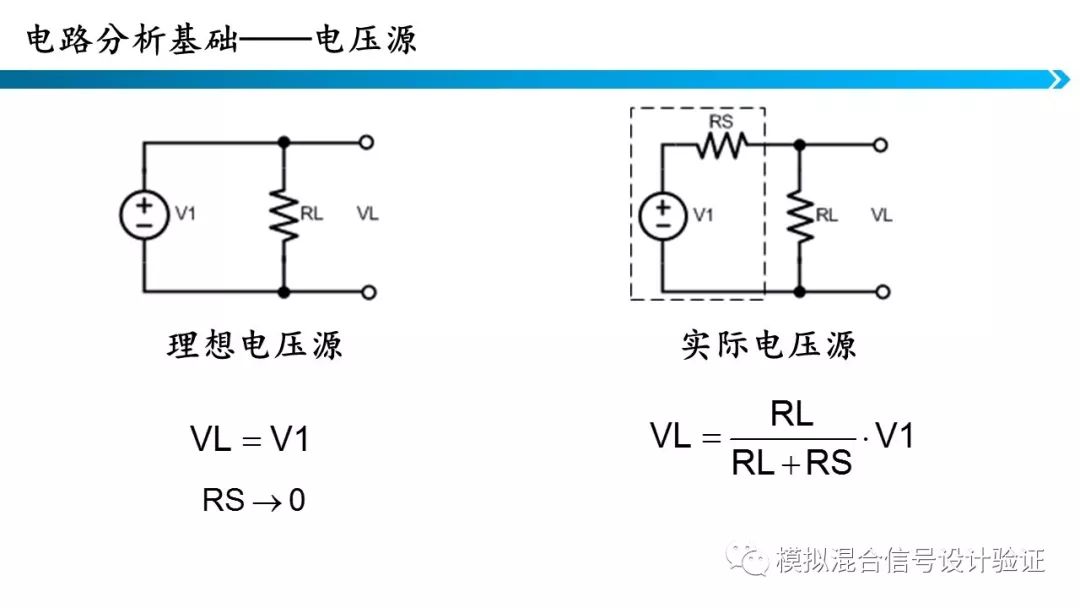
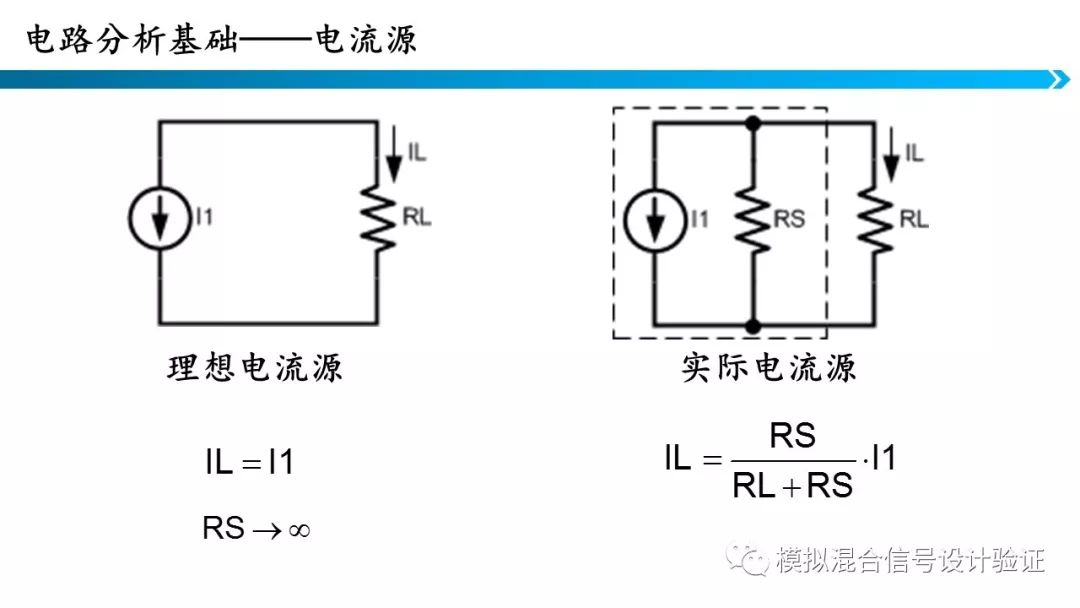
5.电压源和电流源

理想的电压电流源是分析时常用的模型，但实际中用到的电压源和电流源都有内阻。

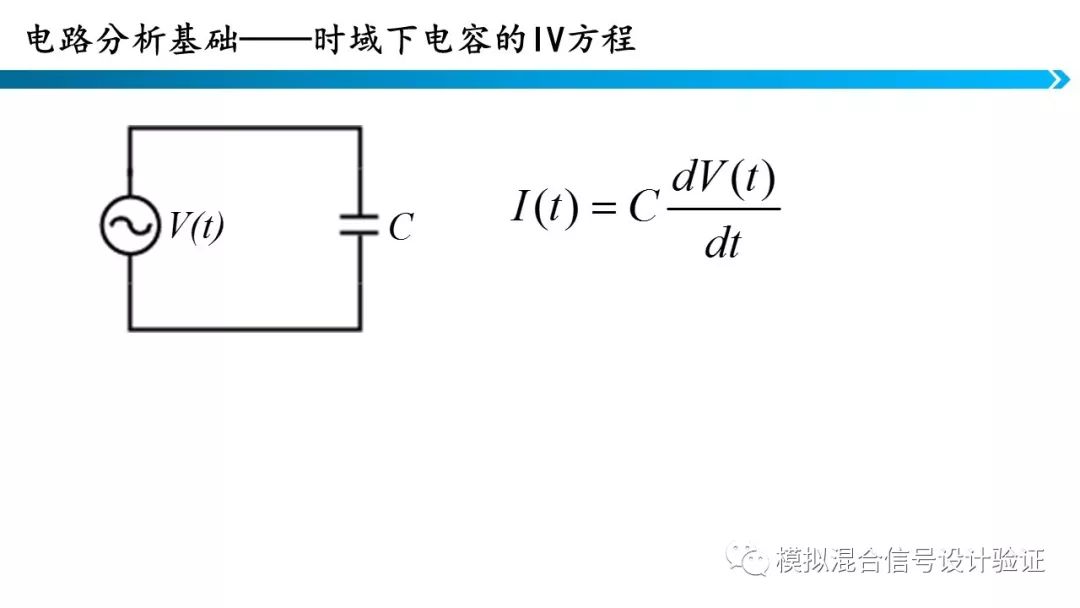
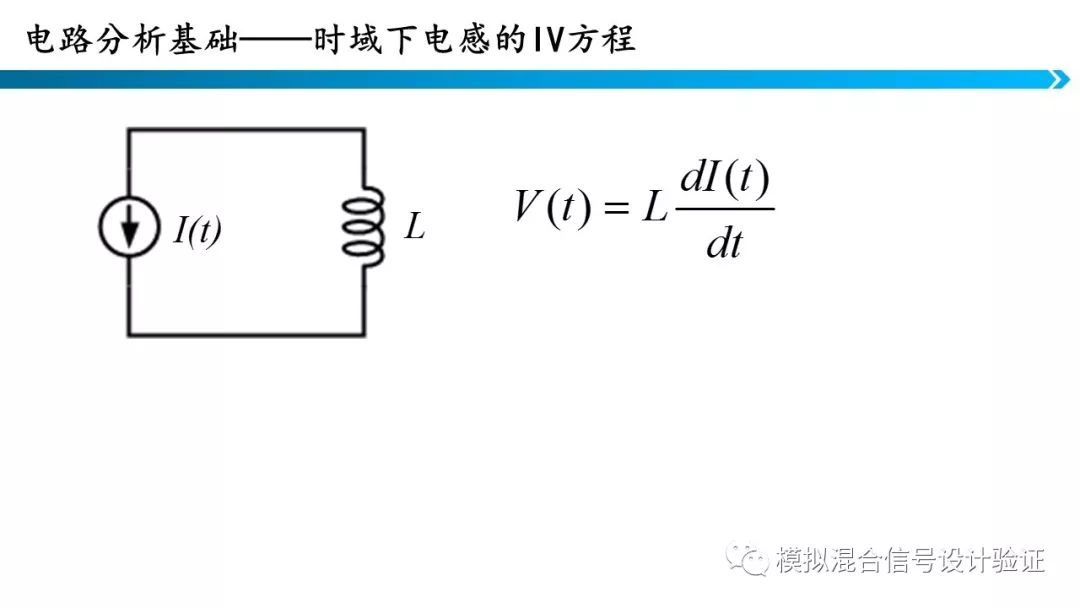
6.电容电感I-V关系

电容电感I-V关系实际上就是电容电感的欧姆定律，只不过由于电容电感的物理特性，方程中出现了微分。但这是在时域分析的结果，如果我们在频域中分析电容电感的I-V关系，就会发现电感的阻抗是正虚数，电容的阻抗是负虚数。

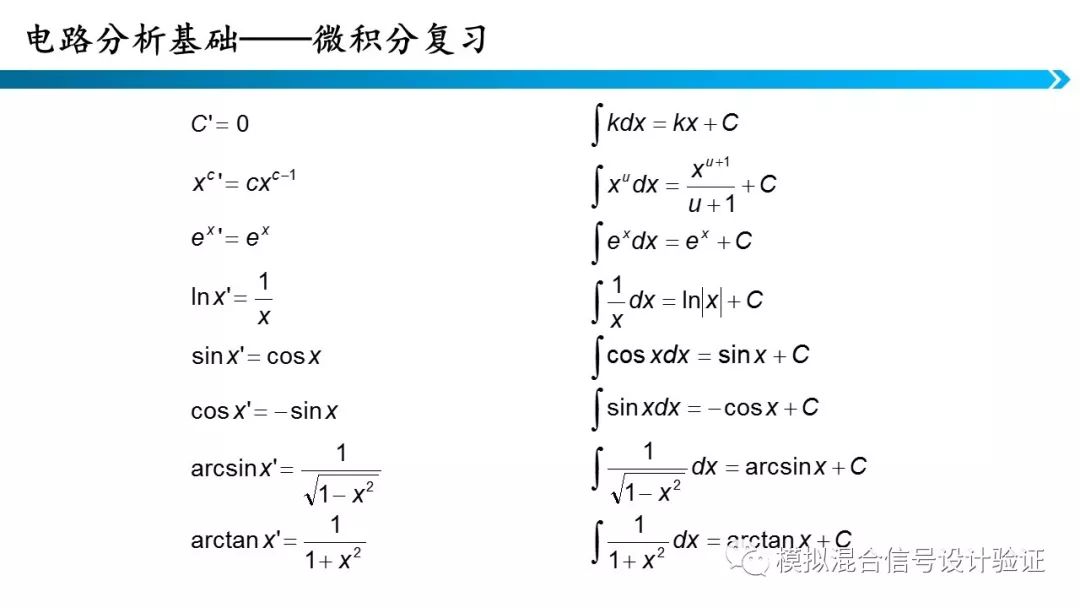
7.微积分的基础知识

有时我们需要在时域列写电路的方程，由于电感电容器件的存在，这些方程往往是微分方程，所以了解微积分的基础知识是必要的。

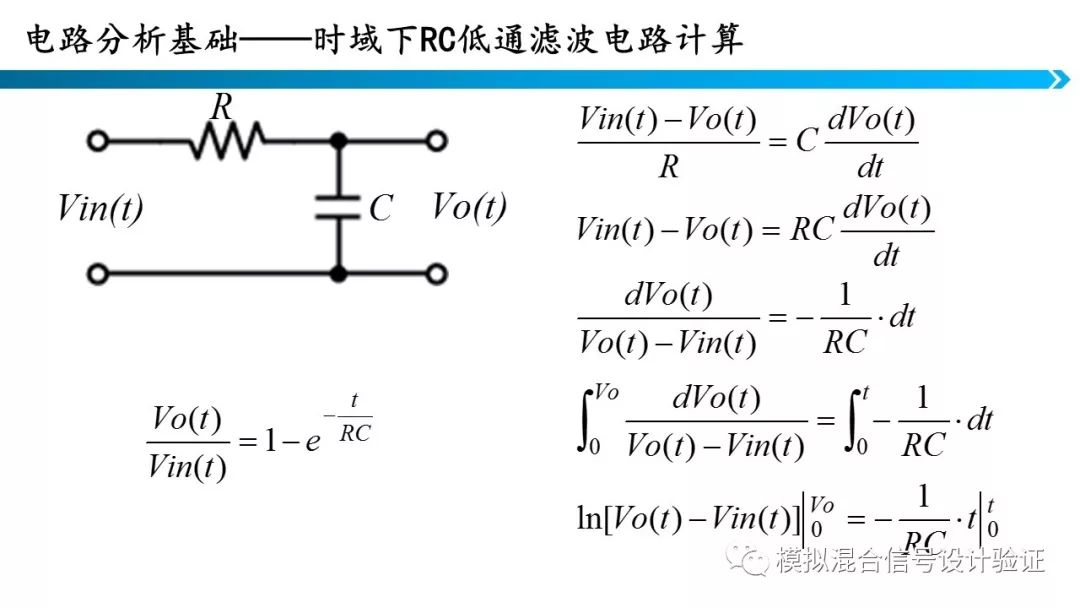
这里举一个低通RC滤波器电路计算的例子。

通过KCL、KVL以及电容电阻的欧姆定律列方程。求解方程组即可。从上面的推导可以看出，如果在时域求解这些方程，就必须要求解复杂的微分方程。有没有什么方法可以只要求解简单的代数方程就能就能得到答案呢？

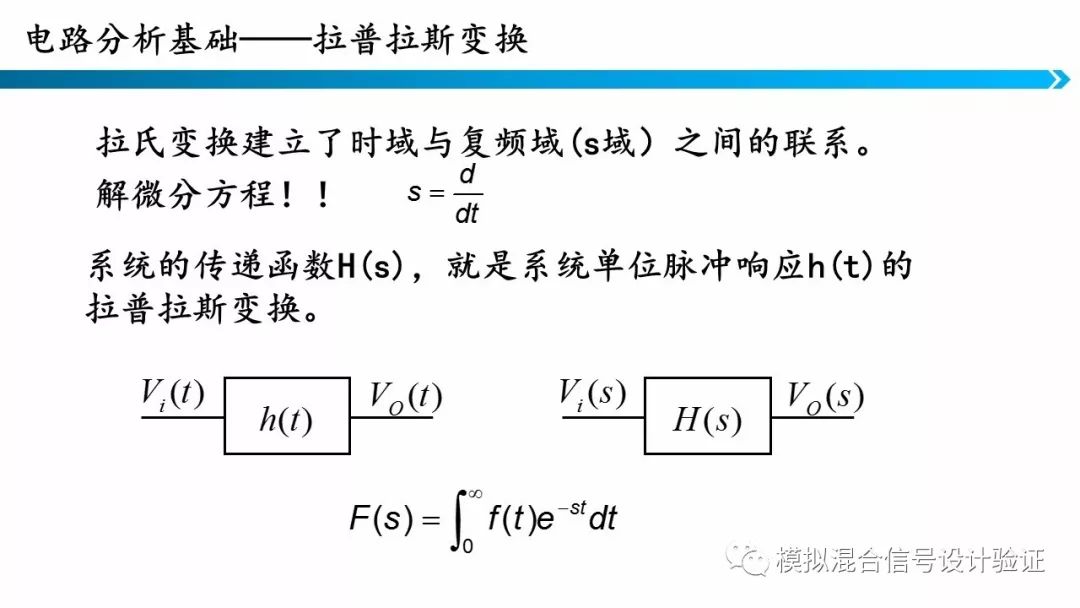
数学家提供了一种叫做拉氏变换的工具，通过拉氏变换，时域微分方程就变成了频域的代数方程。拉氏变换的定义图所示，这里写的比较简单，大家想要进一步了解需要查阅信号与系统书籍。上图中也给出了一些常用的函数对应的拉氏变换。

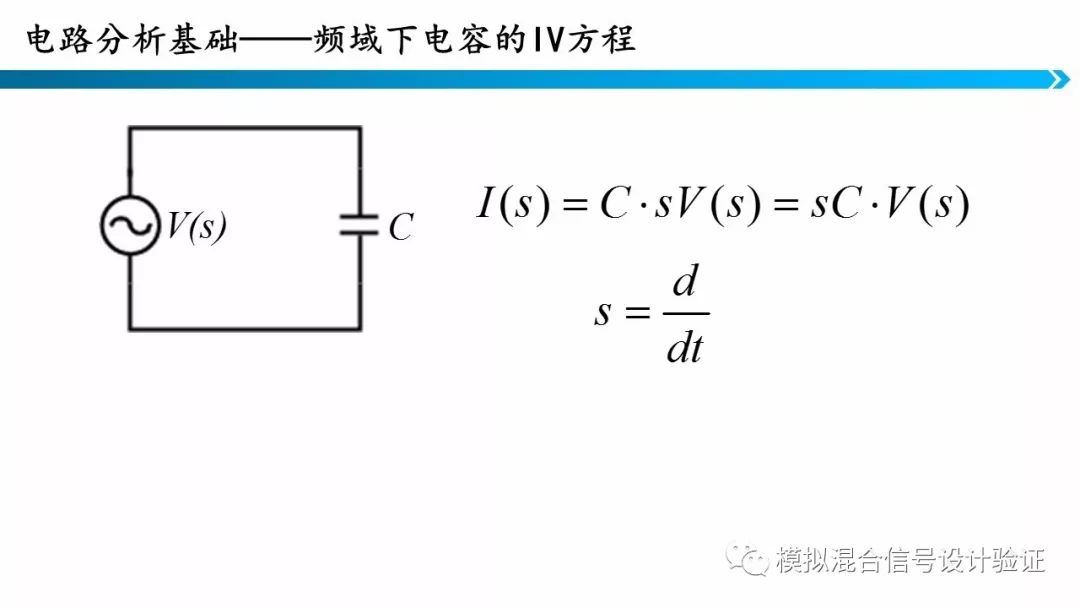
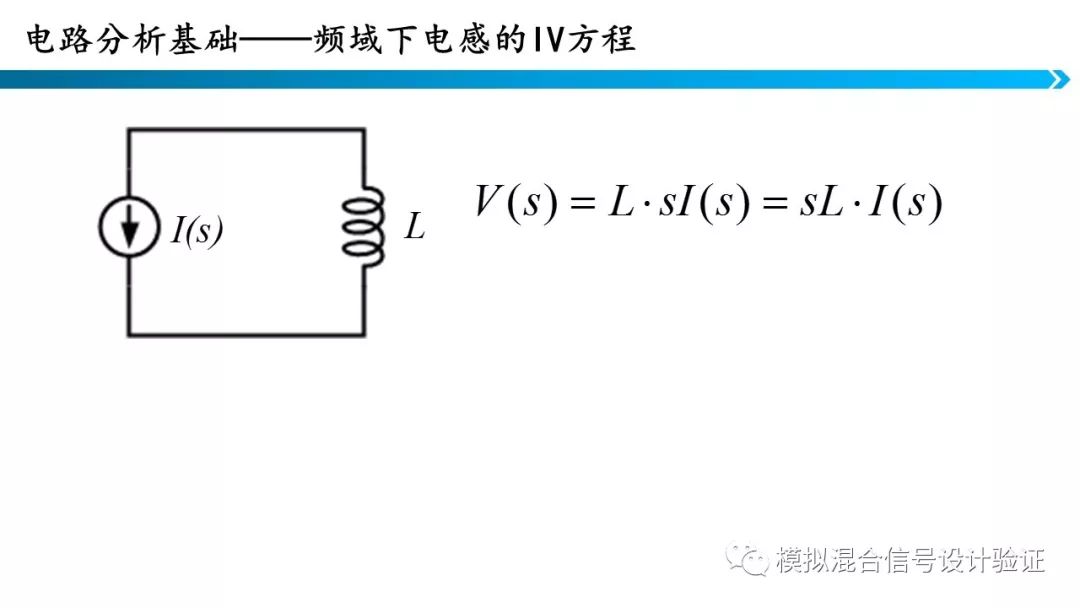
可以看到，在时域电容电感的I-V关系由微分方程描述，在频域就可以用代数方程描述了。

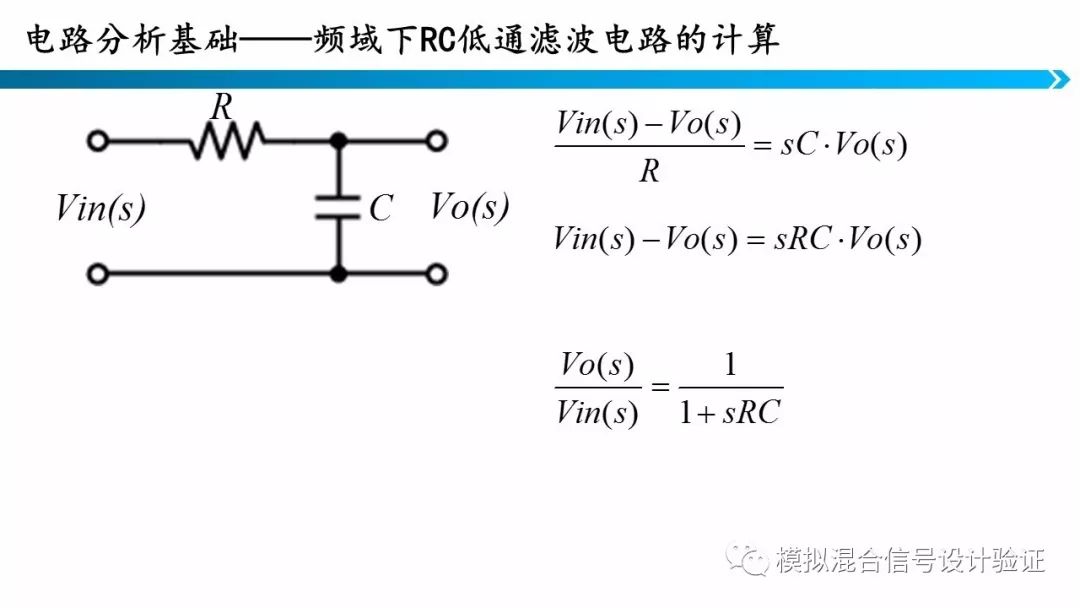
同样的电路，我们在频域分析时就非常简单了。对照上图中的拉氏变换对应表，将运算结果转回时域，可以发现两种运算方法是等价的。

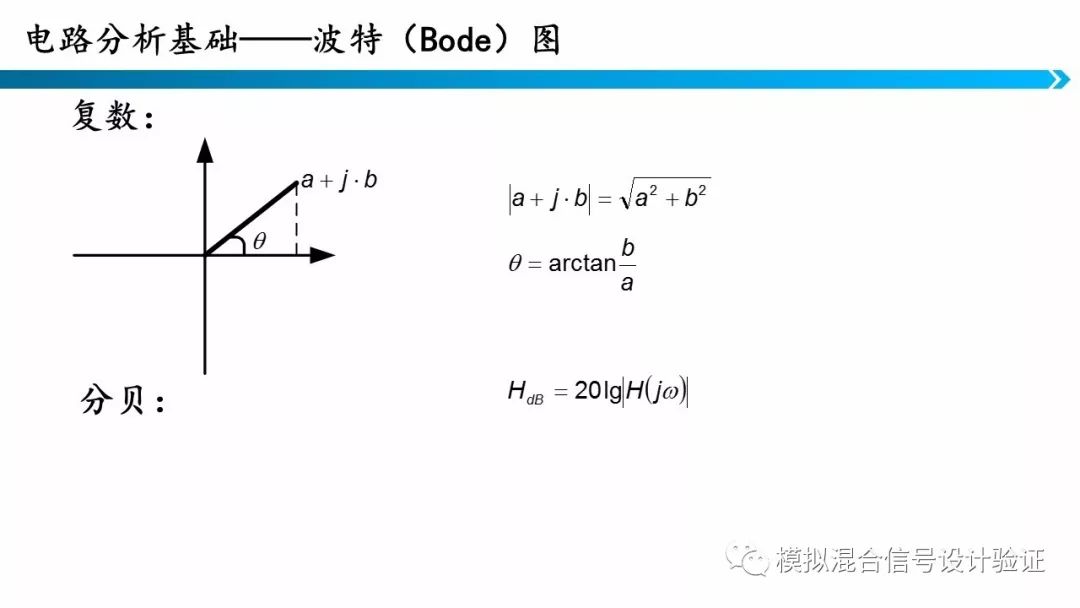
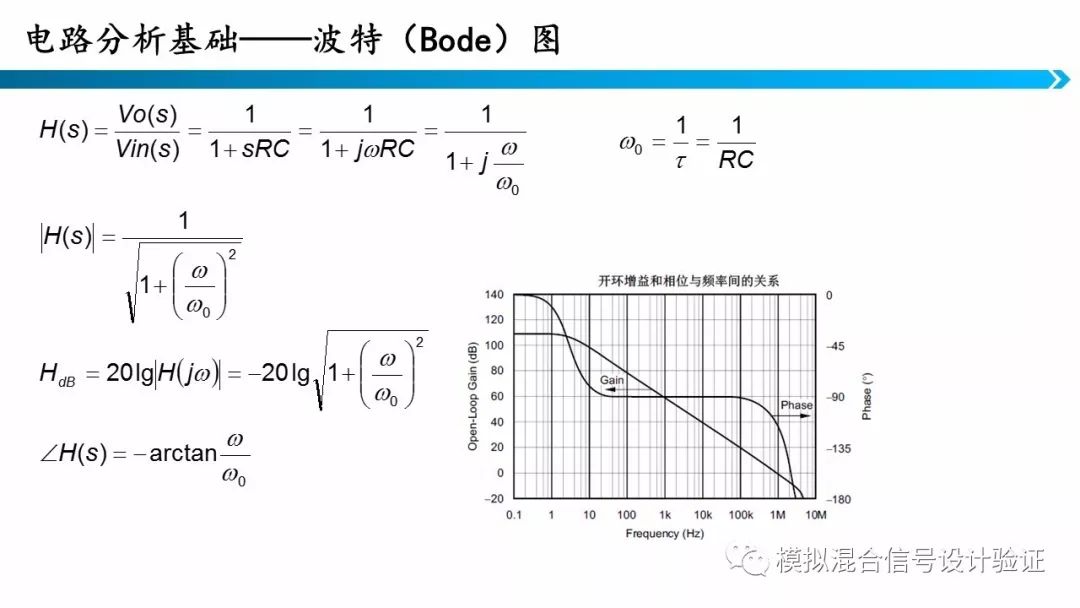
这里我们介绍分析电路常用的另一个工具——波特图，我们常用的波特图由两条曲线构成——幅频曲线和相频曲线。

由于电容电感的存在，电路输入输出的关系常常是一个复数。我们会比较关注复数的模以及相位。我们常用VOUT/VIN表达电路的输出函数，那么该结果的模就是电路的增益，相位就是输出信号相位和输入信号相位的相位差。

第三部分，我们介绍一下应用运算放大器电路的分析。

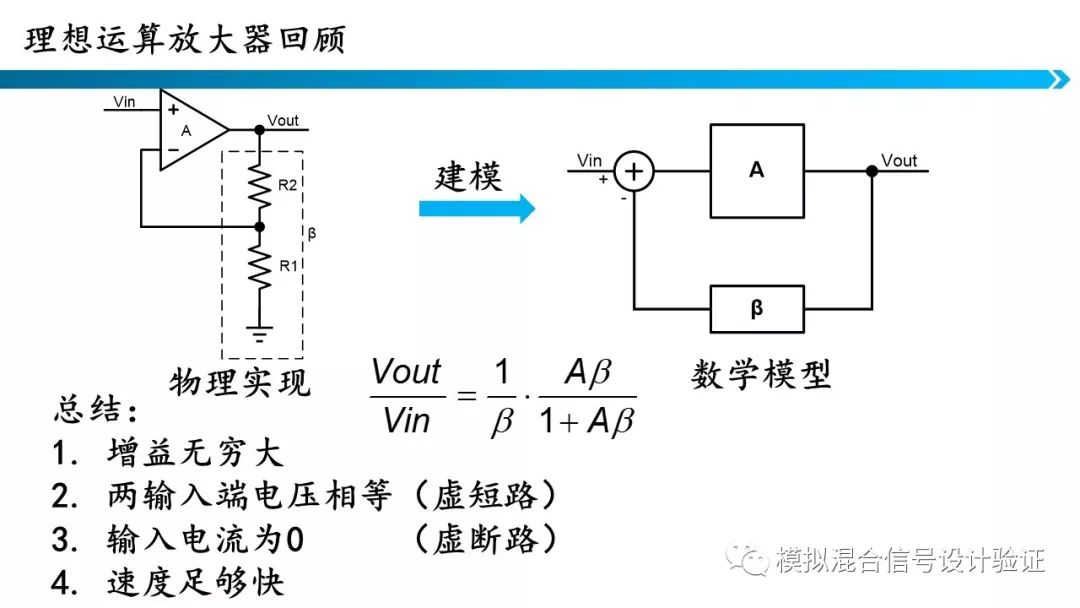
在分析应用运算放大器的电路时，我们经常把运算放大器当成一个黑盒子。应用前面分析的虚短虚断概念分析电路。除了这两点外，其实前面的分析有一点是隐含的，那就是输入输出没有延时，这一点在某些应用中需要被着重关注。

通过运算放大器可以构建很多不同功能的电路。

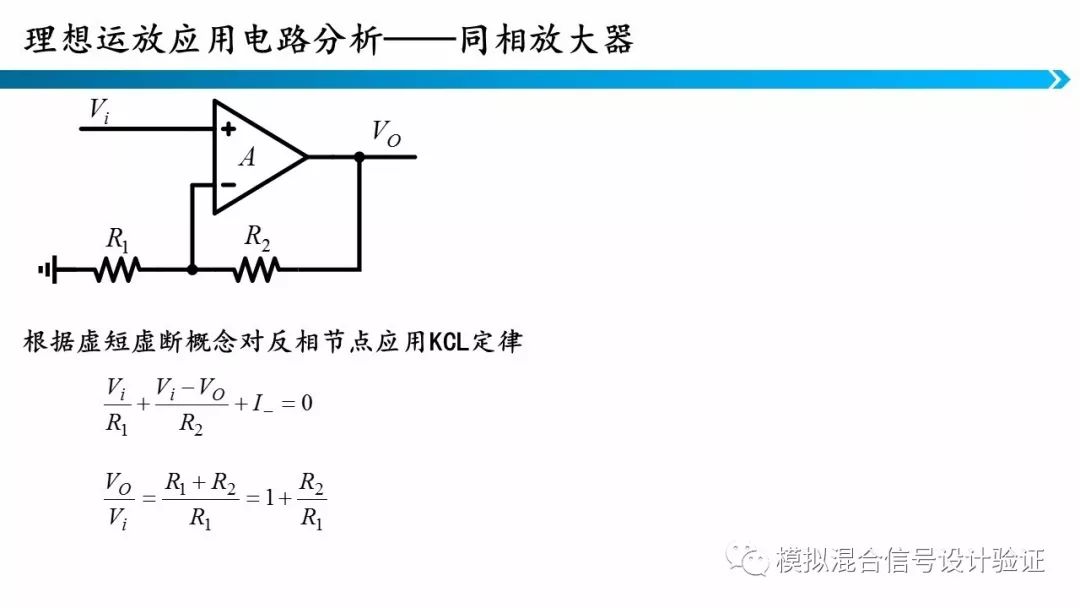
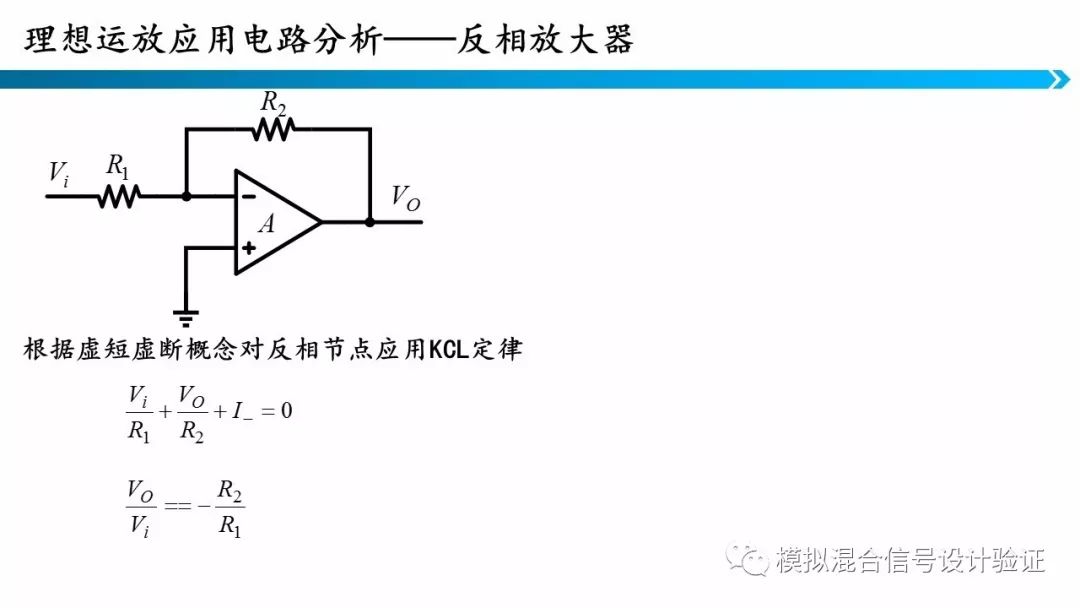
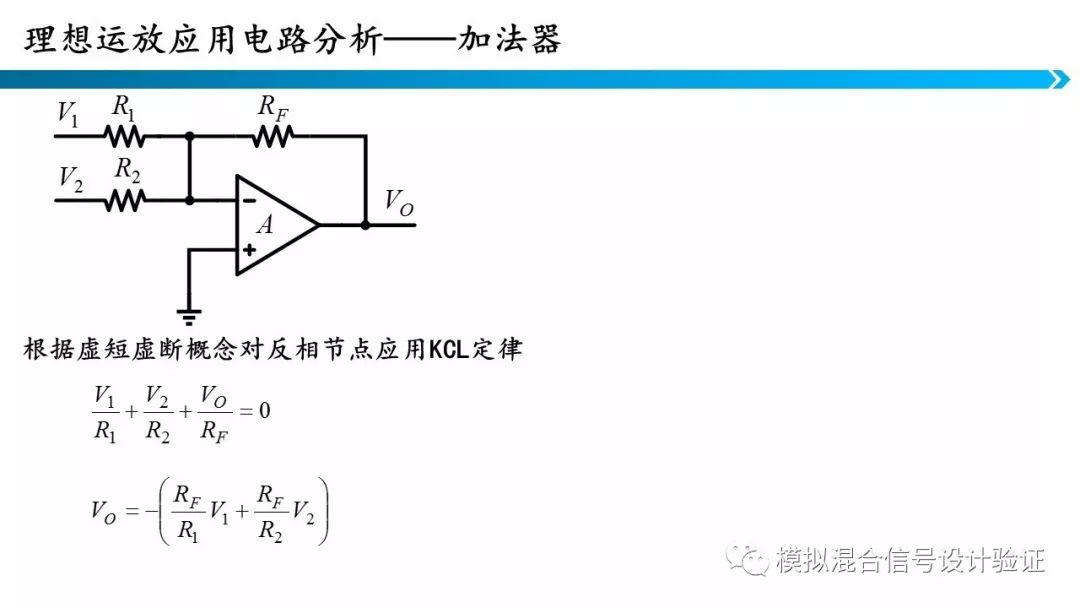
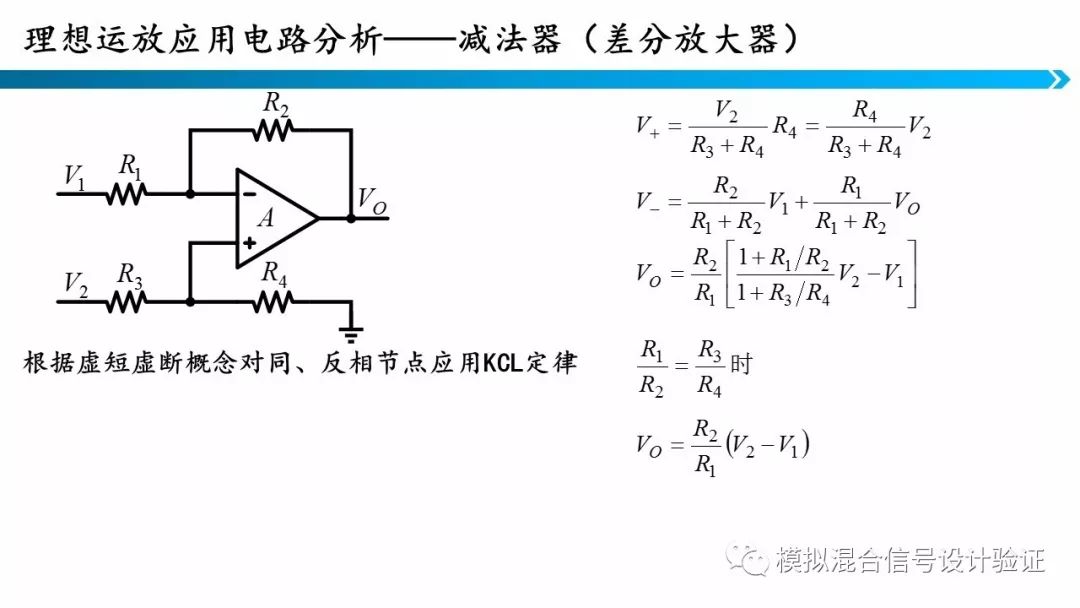
通过结合虚短虚断概念，KCL、KVL以及欧姆定律就可以分析这些电路，同相放大器、反相放大器、加法器、减法器等等都是同样的分析方法。他们的区别就是运算的复杂度逐渐增加了，但是方法是一致的。

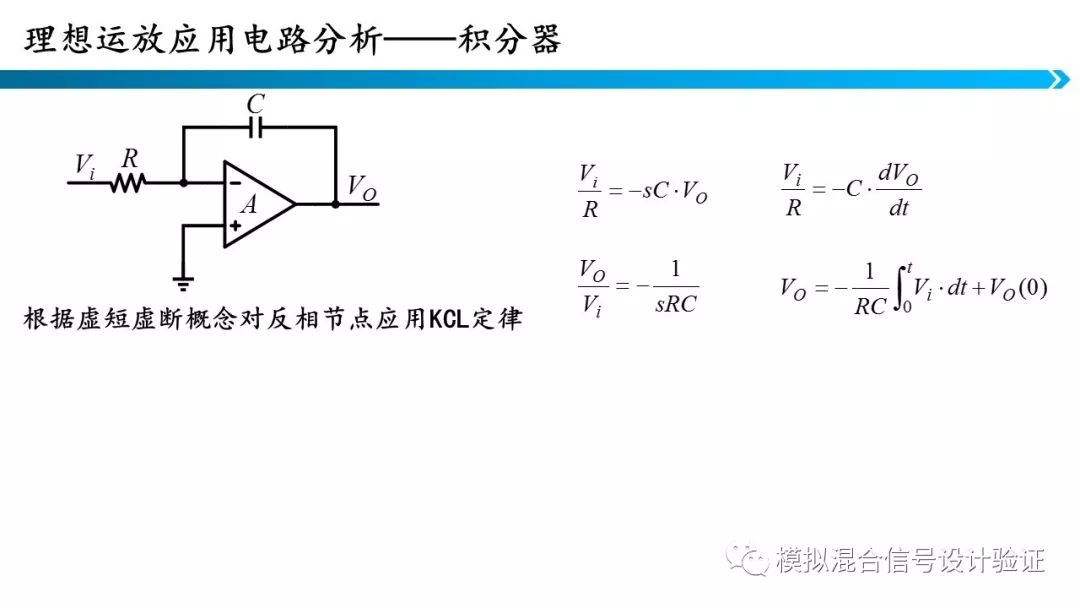
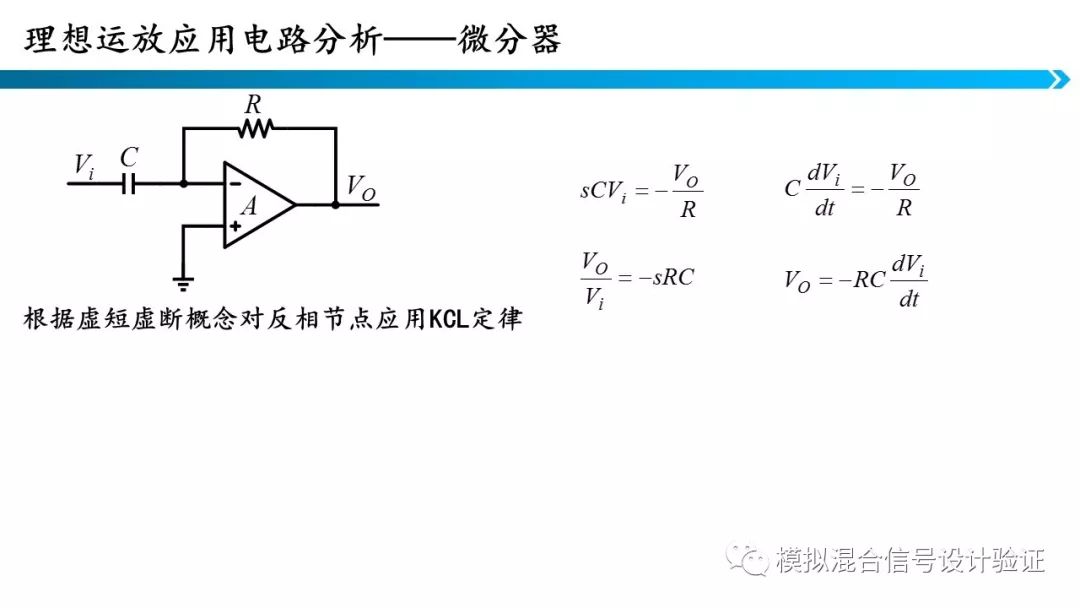
积分器和微分器也是可以通过运算放大器来构建，如果在时域下分析可以看到，电路的微分方程很复杂，但如果通过拉氏变换在频域分析，可以看到公式就简单很多。此外，我们还注意到积分器微分器电路中的对偶关系，积分器的电容电阻颠倒一下就变成微分器了。

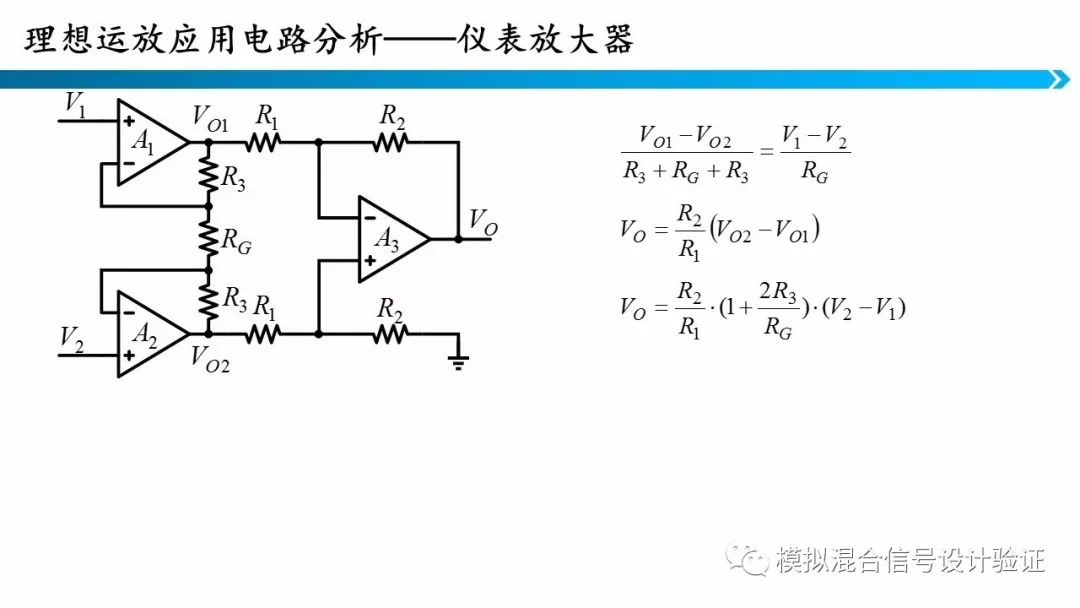
这张PPT展示了一个仪表放大器，可以看到仪表放大器的电路方程复杂度进一步提高。仪表放大器对克服放大器的非理想性很有用，这里就不再展开了。

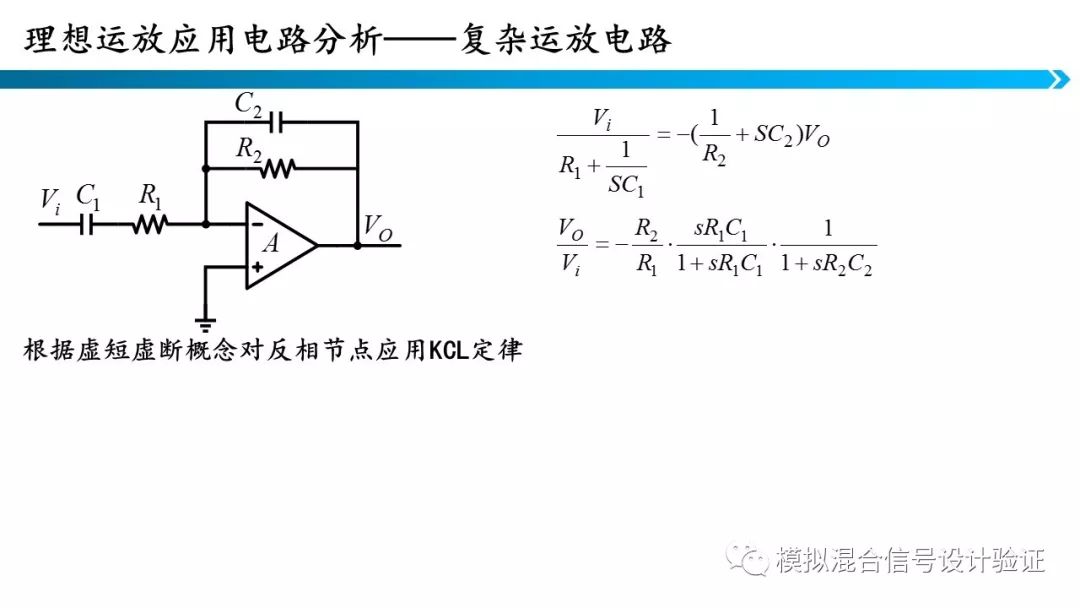
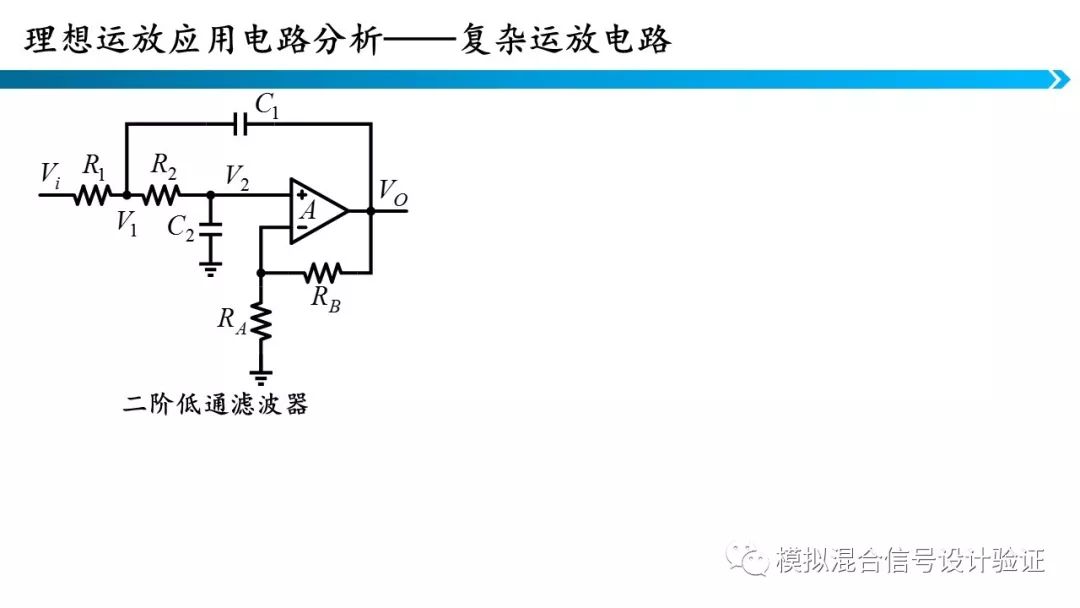
这张PPT展示了一个有源带通滤波器和二阶低通滤波器。如果列写时域方程求解的话，就会出现二阶微分方程，大大增加了计算的难度，但如果我们在频域分析，就只是一个关于s二次方程，求解简单很多。

最后，我们来讨论一下运放的非理想特性和运放的选型。

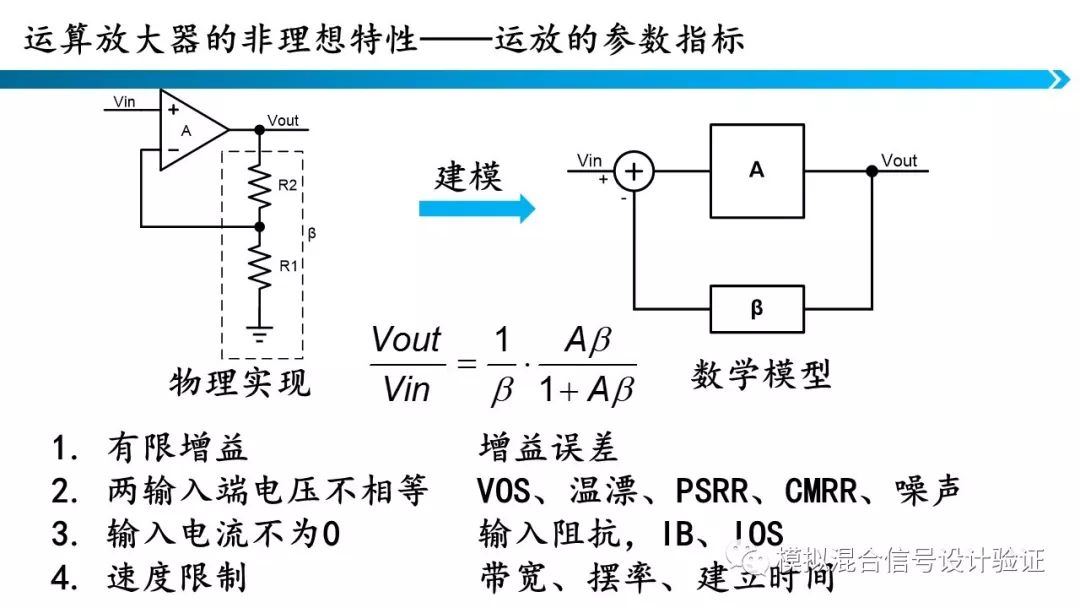
之前我们讨论的都是理想放大器，反复利用的都是虚短虚断概念。但在实际运算放大器中，会有很多非理想特性。首先实际放大器的增益是有限的，那么就会产生增益误差。第二，如果输入两端电压不相等，那么放大器就会存在失调（offset）、温漂、电源电压抑制比（PSRR）、共模电压抑制比（CMRR）、噪声。第三，由于输入电流不为零，带来的影响就是有限的输入阻抗、偏置电流（IB）、输入失调电流（IOS）。最后，由于有限的速度，实际电路中需要考虑带宽、摆率、建立时间等等。所有这些参数都描述了实际放大器的非理想特性。

这一页，给出了一些放大器的分类和选型方法，图中也展示了每一类放大器的特点，但这些参数都不是孤立的而是交叉在一起的，比如低功耗的运放肯定是低速的。

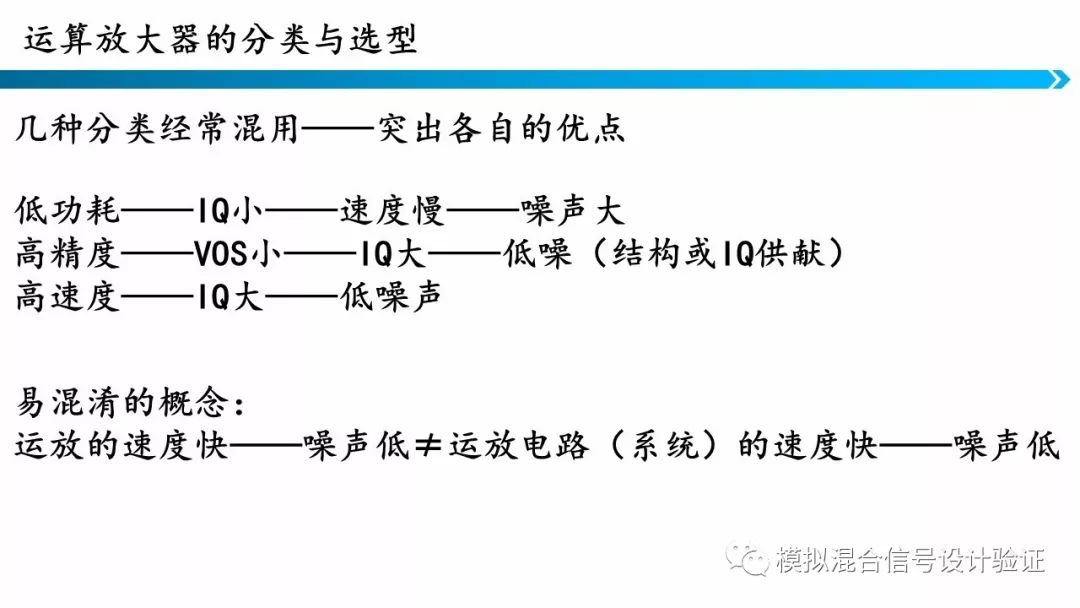
这一页根据运算放大器这些选型，列出了大家常用的一些规律以及大家容易混淆的概念。首先，低功耗意味着速度慢和噪声大，通常用于衡量功耗的参数是静态电流（IQ）。如果要求放大器低噪或者高速，那么不可避免的放大器的功耗会增加。一个容易混淆的概念是运放的速度快、噪声低并不等价于运放构建的系统速度快、噪声低。实际上恰恰相反，如果想要一个系统具有很低的噪声，应当使该系统带宽尽量小以抑制高频噪声。但对于运放来说，大带宽运放的噪声才比较低。