PID算法原理分析及优化

 

欢迎来到森木磊石「技术微课堂」，本期为大家分享经典控制算法之一的PID控制方法。

PID控制方法从提出至今已有百余年历史，其由于结构简单、易于实现、鲁棒性好、可靠性高等特点，在机电、冶金、机械、化工等行业中应用广泛。

下面就跟着小编一起来学习PID算法的原理分析及优化，快来get！

一、PID原理

PID控制方法将偏差的比例（proportional）、积分（integral）、微分（derivative）通过线性组合构成控制量，对被控对象进行控制。

常规的PID控制系统如图所示：

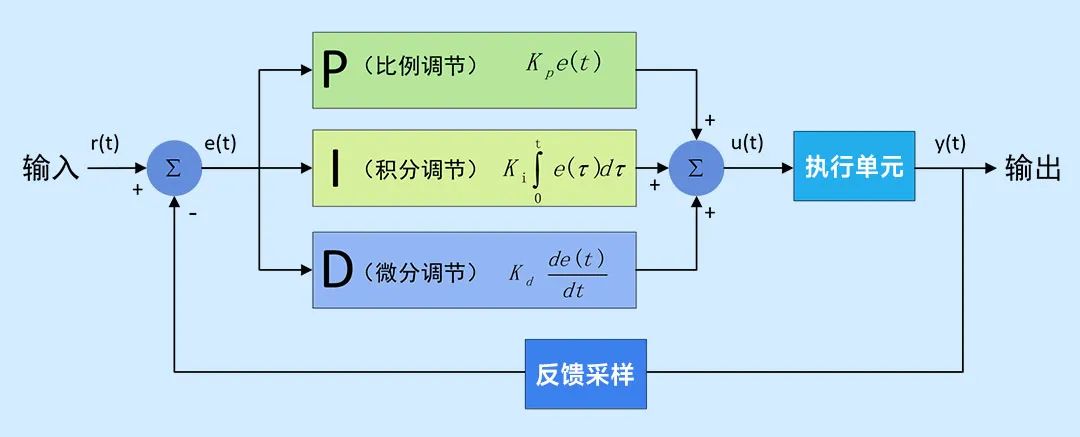
系统的输入r(t)为控制量的目标输出值，输出y(t)为控制量的实际输出值，e(t)为输出量目标值与实际值的偏差量，PID算法的调控是基于e(t)进行的。

比例调节是基于实际值与目标值的偏差量进行线性调节，在系统中表现为Kpe(t)，Kp为比例增益。

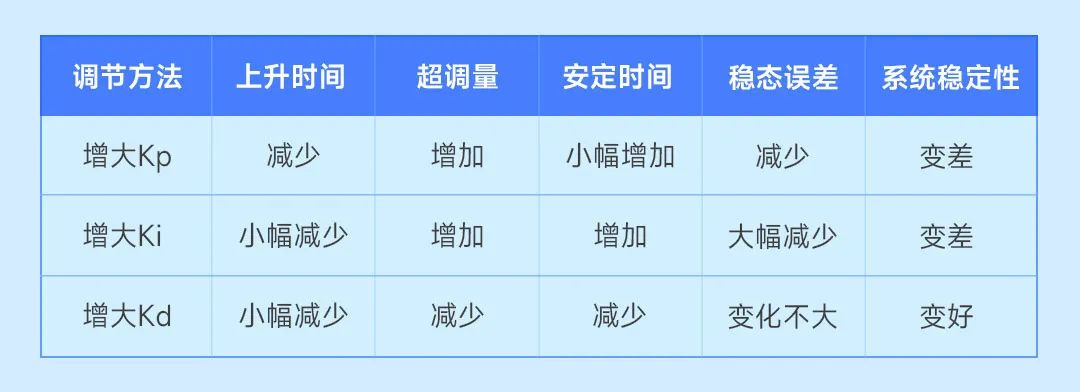
比例增益Kp越大调节作用越激进，输入输出的微小偏差都会造成很大的调节动作；相反的Kp越小调节作用越保守，即使输入输出差异很大系统的调节效果都不太明显。

积分调节是利用历史偏差量的累计对系统输出进行调节，在系统种表示为:

t                                    

Ki∫  e(t)dt，Ki为积分增益。

0                                    

积分调节的意义是消除系统的稳态误差。积分增益Ki越大系统的稳态误差消除的越快，Ki越小系统的稳态误差越不易消除，系统的调节精度越差。但是Ki过大会在响应过程产生较大超调，导致积分饱和现象的产生。

微分调节是基于偏差量的变化速率（偏差求导）对系统输出进行调节，在系统种表示为:

de(t)                     

Kd ————  ,Kd为微分增益。

dt                      

微分调节主要起到阻尼的作用，抑制超调。微分增益Kd越大，系统的稳定性越好，调节过程中曲线波动越小。但是Kd若设置过大会使得系统的调节时间增长，抗干扰性减弱。
 

偏差值在经过三种调节作用后会产生一个控制量u(t)，u(t)将通过执行单元控制输出。系统将利用采样单元将输出反馈给输入端进行偏差量计算。

常规PID控制系统中u(t)与e(t)之间的函数关系如下：

                t                  de(t)

u(t)=Kpe(t) +Ki∫  e(t)dt+Kd ————           式1

             0                        dt

分别调节Kp、Ki、Kd参数对PID控制系统性能的影响如下表所示：

二、数字PID控制

随着计算机技术发展，目前多以微控制器或计算机为运算核心，利用软件程序来实现PID控制和校正，也就是数字PID控制。常用的数字PID控制方法有：位置式PID、增量式PID以及步进式PID等。

01位置式PID

由于计算机的运算是离散的，要想实现数字PID控制首先需要将连续函数进行离散化。

我们用误差的累加替代积分运算，用误差的差分代替微分运算，可得：

k                       

u(k)=Kpe(k)+ki  ∑  e(j)+kd(e(k)-e(k-1))      式2

j=0                      

其中k为采样序列号(k=0,1,2,3......)，e(k)为第k次采样时的误差值，e(k-1)为第k-1次采样时的误差值u(k)为第k次采样时控制量的输出值。在位置式PID中输出u(k)直接控制待控制对象，u(k)的值和控制对象是一一对应的关系。

从式2可以看出，位置式PID需要计算第k次和k-1次的误差，控制器会对偏差进行累加，这样会使得系统的运算量变大，占用内存过多，给计算机带来负担。

同时，控制器的每次输出u(k)都和过去的状态有关，u(k)的大幅变化会导致执行机构的状态大幅变化，系统抗干扰能力差。

为了改善这些问题，有学者提出了数字PID的另外一种实现方法——增量式PID。

02增量式PID

增量式PID的输出是对被控对象的增量∆u(k)，而不是实际的控制量大小。

∆u(k)=u(k)-u(k-1)

        =kp(e(k)-e(k-1))+kie(k)+kd(e(k)-2e(k-1)+e(k-2))

        =a0e(k)+a₁e(k-1)+a₂e(k-2)

其中a0=kp+ki+kd, a₁=-Kp-2kd,a₂=kd。

从上式可以看出增量式PID跟k时刻、k-1时刻、k-2时刻的偏差都有关系，但是不会对偏差进行累积，所以相比位置式PID的计算量要小，也不会跟过去的偏差有关联，所以控制系统的稳定性好。

03步进式PID

当PID系统的设定值发生较大的突变时，系统很容易产生超调，影响其稳定性。为了避免阶跃信号带来的不利影响，有学者提出了步进式PID。

步进式PID不对阶跃信号进行直接响应，而是按照设定的步进规则逐渐增加设定值，使得信号逐步靠近目标值，这样被控对象运行平稳，避免了因突变带来的超调。

这种方法并未改变PID算法结构本身，而是对设定值进行步进处理，使其不产生突变。步进处理方法有很多种，最为常见的是建立一个线性变化函数，确定变化步长，当检测到目标值发生变化后按照步长逐步调整设定值。

Ys=Yn+kT

其中Ys为设定目标值，Yn为当前目标值，T为步长，k为变化系数。当检测到目标值增加时k=1，当目标值不变时k=0，当目标值减小时k=-1。

步进式PID虽然可以减少阶跃信号带来的干扰，但是也会让系统的响应速度变慢，可以调节步长来平衡两者之间的关系。步长越小运行越稳定，系统响应速度越慢，反之亦然。

三、PID算法优化

01积分饱和优化处理

若系统持续存在一个方向的偏差时，PID控制器的输出由于积分作用不断累加而增大，从而导致控制器输出产生超调进入饱和区。

当系统出现反向偏差时，由于输出饱和而不能对反向的偏差进行快速响应，这种现象称为积分饱和。

常用抑制PID积分饱和方法有：积分分离法、遇限削弱积分法以及变速积分法等。

//积分分离法

当系统检测到偏差e(k)较大时，取消积分环节，当被控量接近给定值时，误差减小，此时恢复积分环节。这样既不影响控制器的动态性能，又能避免出现严重超调或持续振荡现象。

//变速积分法

根据系统的偏差e(k)大小对积分速度进行调整，当e(k)绝对值很大时减慢积分速度，当e(k)绝对值很小时加快积分速度。在积分饱和时减小积分时间可以达到抑制积分饱和的效果，增强系统的适应性。

//遇限削弱积分法：

当检测到控制量u(k)进入饱和区时不再进行积分项累加，而执行削弱积分的运算。这样不会产生过多的超调量，当需要反向调节时能较快地响应，避免输出长时间停留在饱和区。

02微分项优化处理

PID算法中微分项与偏差的变化速率有关。如果系统存在频率较高的干扰或突变等情况时，微分项的数值会不断跳变，使控制过程产生系统振荡，影响控制系统的稳定性。

常用的微分环节优化方法如下：
 

//微分先行：

微分项对测量值产生的偏差起作用，而不是对设定值起作用。这样可以避免设定值的变化而产生较大的调节波动，抑制高频干扰引起的系统振荡。

//不完全微分：

不完全微分是在微分作用后引入一阶惯性环节，使得在偏差作阶跃式变化时产生的微分调节量，以一种较为平缓的方式输出。这样在不减小微分调节作用的前提下，降低因为偏差突变产生的波动。

//受控微分法：

受控量微分PID算法是对控制器的输出值进行微分，而不是对系统响应的实际输出值进行微分，可避免由于系统设定值频繁变化或执行器的振荡产生的系统响应超调量过大。

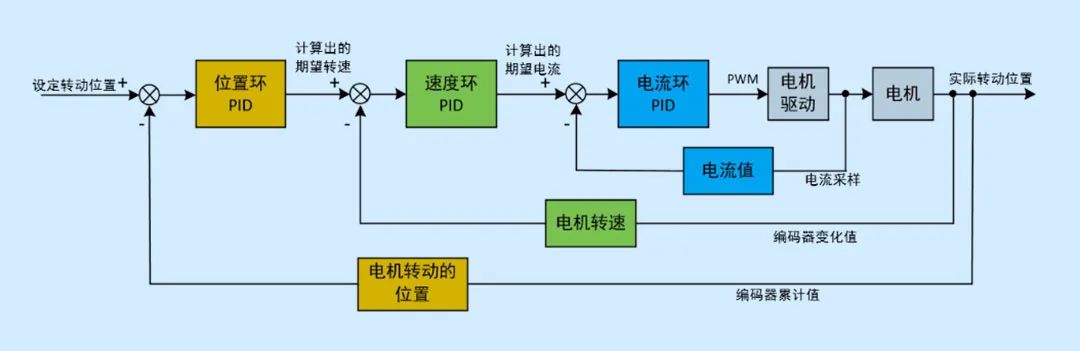
03串级PID

所谓串级PID，就是采用多个PID控制器串联工作，外环控制器的输出作为内环控制器的设定值，由内环控制器的输出去操纵外环控制器，从而实现外环被控量的控制效果。串级PID能够有效改善控制质量，在过程控制中应用广泛。

控制系统以外环控制器为主导，保证外环主变量稳定为目的，两个控制器协调一致，互相配合。外环控制器按负荷和操作条件的变化不断纠正内环控制器的设定值，使内环控制器的设定值适应负荷和操作条件的变化。

在电机控制中串级PID十分常见，常用的位置环+速度环+电流环控制结构如图。

在PID控制方法中P、I、D是三种不同的调节作用，在实际应用时可根据需求对三种调节作用进行灵活组合，这也是PID控制方法的魅力所在，它的结构决定了它在实际应用中的多样性与灵活性。

本篇主要从PID原理、数字PID实现方式以及算法优化方面进行了简单介绍，希望能够对大家学习PID算法有所帮助。