

力控机器人控制方法的框架及其性能分析
描述
力控机器人常采用柔顺控制算法与人/环境/机器人之间进行直接或间接的物理交互,那么,柔顺控制能够操纵被控系统的柔性特性和动态行为,实现方式可以分为被动柔顺和主动柔顺,具体分类如下图所示:
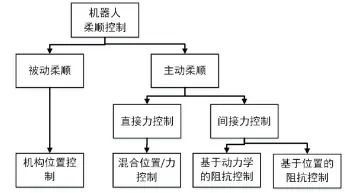
力控机器人交互控制框架是用于实现机器人与外部环境或操作者之间的力互动的控制系统。
在力控机器人交互控制中,主要涉及直接力控制、阻抗控制和导纳控制三种主要方法。下面是这些控制方法的框架及其性能分析:
1. 直接力控制框架:
力/力矩传感器:用于测量机器人与环境之间的力和力矩。
力/力矩控制器:根据传感器测量值和期望的力/力矩指令,生成控制指令以实现期望的力互动。
运动控制器:用于控制机器人的关节或末端执行器,以实现所需的运动轨迹。
环境建模与识别:用于对环境进行感知和识别,以帮助机器人适应环境变化。

性能分析:
•力跟踪性能:评估力控制器的能力,以实现期望的力跟踪。
•运动轨迹跟踪性能:评估运动控制器的能力,以实现期望的运动轨迹跟踪。
•动态响应性能:评估系统对外部力变化的响应速度和稳定性。
•力/位置误差分析:分析力控制和位置控制之间的误差,以评估系统的精度和稳定性。
•稳定性分析:通过线性稳定性分析或Lyapunov稳定性分析等方法,评估力控制系统的稳定性。
2. 阻抗控制框架:
力/力矩传感器:用于测量机器人与环境之间的力和力矩。
阻抗控制器:根据传感器测量值和期望的力/力矩指令,生成控制指令以实现期望的阻抗互动。
运动控制器:用于控制机器人的关节或末端执行器,以实现所需的运动轨迹。
环境建模与识别:用于对环境进行感知和识别,以帮助机器人适应环境变化。
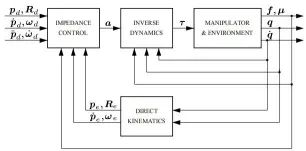
性能分析:
•阻抗响应性能:评估阻抗控制器对外部力变化的响应速度和稳定性。
•阻抗参数分析:分析阻抗控制器中的参数对系统性能的影响,如阻尼、刚度和质量等参数。
•阻抗稳定性分析:评估阻抗控制系统的稳定性,包括阻抗稳定性边界和阻抗参数的稳定性范围。
•动态性能分析:分析阻抗控制器对不同频率的外部力变化的动态响应性能。
•阻抗控制精度分析:评估阻抗控制器在实现期望的阻抗响应时的精度和稳定性。
以下为阻抗控制简单实现的MATLAB程序:
% 定义阻抗控制参数
M = 5;
B = 10;
K = 20;
% 定义初始位置和速度
x = 0;
xdot = 0;
% 定义时间步长和仿真时间
dt = 0.01;
T = 5;
% 初始化位置和速度数组
x_arr = zeros(1, T/dt);
xdot_arr = zeros(1, T/dt);
% 进行阻抗控制仿真
for i = 1:T/dt
% 计算外部力
F_ext = 10 * sin(i*dt);
% 计算加速度
xddot = (F_ext - B*xdot - K*x) / M;
% 更新位置和速度
xdot = xdot + xddot*dt;
x = x + xdot*dt;
% 存储位置和速度
x_arr(i) = x;
xdot_arr(i) = xdot;
end
% 绘制位置和速度图像
t = 0:dt:T-dt;
subplot(2,1,1)
plot(t, x_arr)
title('Position')
subplot(2,1,2)
plot(t, xdot_arr)
title('Velocity')
仿真结果如下:
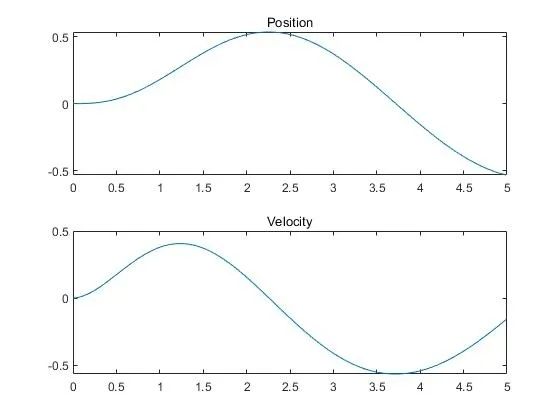
对于二连杆机械臂的阻抗控制,需要考虑机械臂的动力学模型。需要更多的信息来确定机械臂的参数和控制目标:
% 定义阻抗控制参数
Md = diag([5, 5]);
Bd = diag([10, 10]);
Kd = diag([20, 20]);
% 定义机械臂质量和初始位置
m1 = 1;
m2 = 1;
l1 = 1;
l2 = 1;
q = [0; 0];
qdot = [0; 0];
% 定义时间步长和仿真时间
dt = 0.01;
T = 5;
% 初始化位置数组
q_arr = zeros(2, T/dt);
% 进行阻抗控制仿真
for i = 1:T/dt
% 计算外部力矩
tau_ext = [10 * sin(i*dt); 5 * cos(i*dt)];
% 计算关节惯量矩阵
M = [(m1+m2)*l1^2 + m2*l2^2 + 2*m2*l1*l2*cos(q(2)), m2*l2^2 + m2*l1*l2*cos(q(2));
m2*l2^2 + m2*l1*l2*cos(q(2)), m2*l2^2];
% 计算离心力与科氏力矩阵
C = [-m2*l1*l2*sin(q(2))*qdot(2), -m2*l1*l2*sin(q(2))*(qdot(1)+qdot(2));
m2*l1*l2*sin(q(2))*qdot(1), 0];
% 计算重力矩阵
G = [(m1+m2)*l1*9.8*cos(q(1)) + m2*l2*9.8*cos(q(1)+q(2));
m2*l2*9.8*cos(q(1)+q(2))];
% 计算期望加速度
qddot_d = Md (tau_ext - Bd*qdot - Kd*q);
% 计算控制力矩
tau = M*qddot_d + C*qdot + G - Bd*qdot - Kd*q;
% 更新位置和速度
qddot = M (tau + tau_ext - C*qdot - G);
qdot = qdot + qddot * dt;
q = q + qdot * dt;
% 存储位置
q_arr(:,i) = q;
end
% 绘制位置图像
t = 0:dt:T-dt;
subplot(211)
plot(t, q_arr(1,:))
title('Joint 1 Position')
subplot(212)
plot(t, q_arr(2,:))
title('Joint 2 Position')
-
力控机器人的控制框架和性能评估2023-11-09 1245
-
机器人阻抗控制有几种方法2023-11-08 2224
-
通过多轴工业机器人来聊聊机器人控制系统以及控制器的实现2023-02-24 2448
-
机器人是什么?2022-03-31 22107
-
刚柔软机器人设计与仿真分析实例解析2021-09-02 4365
-
差速移动机器人轨迹跟踪控制方法2021-09-01 1784
-
盘点工业机器人四种控制方法2020-07-30 11862
-
竞赛机器人制作技术(电路设计、编程方法、算法解析)2019-12-25 5366
-
如何设计智能灭火机器人控制器?2019-07-31 3828
-
机器人基础书籍2019-05-22 3545
-
机器人、协作机器人和移动机器人,你分的清楚吗2018-10-30 3986
-
先进机器人控制2017-09-19 4389
-
【机器人在线】工业喷涂机器人误差修正方法发展趋势2017-07-13 2677
-
工业机器人的基本结构2015-01-19 9228
全部0条评论

快来发表一下你的评论吧 !

