

机器人时间缩放法原理
描述
时间缩放法的初衷是用于修改轨迹,避免轨迹违反系统饱和约束限制的,我们先阐述其原理,然后将其用于实现速度曲线时间同步。
在一些应用场景中需要考虑驱动系统的饱和限制约束,为了保证规划的期望轨迹不违反此类饱和限制,必须对原始的轨迹进行修改。
由于那些运动速度、加速度和力矩超过允许范围的运动轨迹在实际中无法执行,因此此类运动轨迹在实际工程中应予以避免。实际中可以将饱和区分为如下两类。
(1)运动学饱和:规划后轨迹的速度或加速度超过了驱动系统所能实现的临界速度或临界加速度。
(2)动力学饱和:此列饱和发生于驱动系统所需的驱动力矩(超过驱动系统所能提供的临界力矩)不可行的情形。
特别地,由于多机械系统动力学的非线性耦合性,动力学饱和现象往往出现于此类多轴机械系统(如工业机器人)中。
如果在轨迹规划阶段并未提前考虑上述运动学饱和及动力学饱和限制,那么有必要在系统跟踪运动轨迹之前验证运动轨迹的可行性,并采取必要措施(如增加轨迹的时间长度)来防止违反上述饱和限制。
首先,给定一条轨迹:
q=q(t)
接下来引入一个新的与时间t有关的时间变量′t′ 可使得上面轨迹变快或变慢,或者更一般地,可以修改轨迹的速度和加速度等,其中 t和
′t′之间具有如下严格的函数关系:
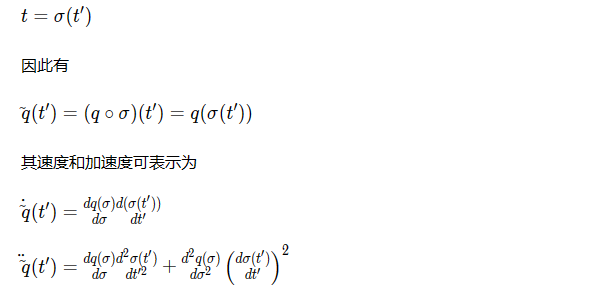

为了简便起见,上述关系可以重新写成如下形式:


声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
机器人时代将来临,谁的饭碗已“告急”?2016-11-01 633
-
机器人时代到来临——操控人才在何方?2015-03-02 3865
-
机器人与未来2015-12-29 6551
-
华硕Zenbo,机器人时代来了?2016-06-06 4813
-
身处“机器人时代”,我们该如何相处?2017-06-20 2911
-
选购工业机器人要了解哪些技术参数?2017-08-26 3542
-
已开奖——【送书福利】机器人时代已来!送你几本机器人学硬核好书2020-11-16 8710
-
SCARA工业机器人相关资料推荐2021-07-01 1367
-
abb机器人电源模块短路板短路故障处理2021-09-17 4154
-
机器人时代已正式到来2018-07-18 3049
-
智能机器人时代哪些工作处于危险之中?2020-10-11 4312
-
机器人时代:机器人市场增加,人类未来终将会与各种机器人共存!2020-10-26 2476
-
服务机器人时代,真的要到来了吗2022-06-09 1550
-
焊接机器人编程方法及流程技巧2023-01-13 15427
-
机器人梯形加减速轨迹时间缩放2023-11-10 1479
全部0条评论

快来发表一下你的评论吧 !

