机器人梯形加减速轨迹时间缩放

基于上面的原理，不管是q(t)是何种加减速算法生成，都可以使用上面的时间缩放法进行时间同步，下面以梯形减速为例进行说明,流程如下图所示。

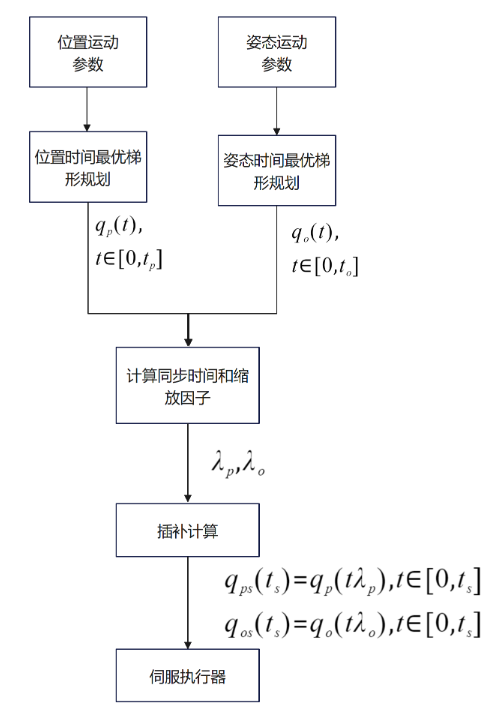
从流程图中可以看出，只需在插补环节对时间较小的轨迹进行时间缩放即可，整个流程计算量很少。

下面给出不同参数下的几个算例，实现代码在本文末尾。

算例1

有匀速段，位置与姿态位移量相差不大。

%位置梯形参数
vs=10;%起步速度
vmax=50;%最大速度
ve=20;%末速度
amax=500;%加速度
dmax=400;%减速度
L=10;%位移
Ts=0.001;%插补周期
%姿态参数
vs=5;
vmax=40;
ve=15;
amax=300;
dmax=200;
L=8;
Ts=0.001;

算例2

位置与姿态位移量相差不大，均没有匀速段。

%位置梯形参数
vs=10;%起步速度
vmax=50;%最大速度
ve=20;%末速度
amax=500;%加速度
dmax=400;%减速度
L=5;%位移
Ts=0.001;%插补周期
%姿态参数
vs=5;
vmax=40;
ve=15;
amax=300;
dmax=200;
L=2;
Ts=0.001;

算例3

位置与姿态位移量相差很大,位移是姿态的10倍，位移有匀速段，姿态没有匀速段。

%位置梯形参数
vs=10;%起步速度
vmax=50;%最大速度
ve=20;%末速度
amax=500;%加速度
dmax=400;%减速度
L=20;%位移
Ts=0.001;%插补周期
%姿态参数
vs=5;
vmax=40;
ve=15;
amax=300;
dmax=200;
L=2;
Ts=0.001;

算例4

位置位移量大于0，姿态位移量为0，同步前姿态运行时间就是0，所以其轨迹就是一个点，在左图中看不到。时间同步后，姿态运行时间是与位置相同，只是速度和加速度始终是0。

%位置梯形参数
vs=10;%起步速度
vmax=50;%最大速度
ve=20;%末速度
amax=500;%加速度
dmax=400;%减速度
L=20;%位移
Ts=0.001;%插补周期
%姿态参数
vs=5;
vmax=40;
ve=15;
amax=300;
dmax=200;
L=0;
Ts=0.001;

算例5

连续两段轨迹，同步前衔接速度是相等没有跳变的。同步后衔接速度发生了跳变，不连续。这是因为两段轨迹的缩放因子λ不相等

导致衔接处速度发生了跳变，这是时间缩放法的缺点，因此，时间缩放法不适用于衔接速度非零的连续轨迹时间同步。