

如何实现对机器人接触力的数据滤波
描述
下面举一些例子,实现对机器人接触力的数据滤波!
首先是导入数据:
clc
clear all;
close all;
X = xlsread('E:程序test~六维力数据.csv');%导入数据
A=X(:,1);B=X(:,2);C=X(:,3);D=X(:,4);E=X(:,5);F=X(:,6);%提取力数据
%% 滤波
x=A;
N=1347; %时域点数
fs = 100; % 重采样频率
T = 1/fs; % 周期
n = 5; % 1Hz频率被分成n段
% N = fs*n; % 因为1Hz频率被分成了n段,所以频谱的x轴数组有fs*n个数
f = (0: N-1)*fs/N; % 将fs个频率细分成fs*n个(即原来是[0, 1, 2, …, fs],现在是[0, 1/N, 2/N, …, (N-1)*fs/N])
t = (0: N-1)*T; % 信号所持续的时长(N个周期)
nHz = 10; % 画的频谱的横坐标到nHz
Hz = nHz*n; % 画的频谱的横坐标的数组个数
%% 绘制原始信号时频图
figure
subplot(211),plot(x,'k'),title('原始信号时域'),xlabel('采样点/n'),ylabel('力或力矩'); % 绘制原始信号时域
fx = abs(fft(x-mean(x)))/(N/2); % 傅里叶变换
subplot(212),plot(f(1:Hz), fx(1:Hz),'k'),title('原始信号频谱图'),xlabel('频率/Hz'),ylabel('幅值'); % 绘制原始信号频域
可以得到如下结果:
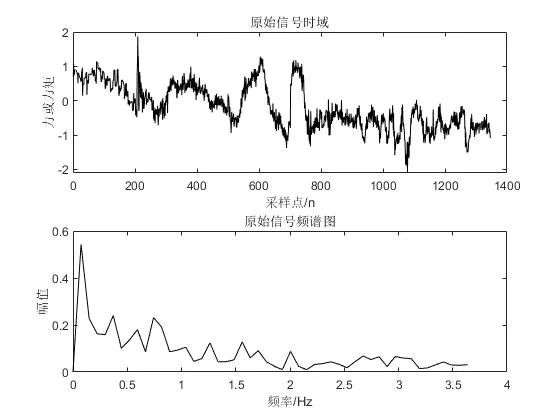
通过傅里叶变换可以得到接触力信号频域上的内容。
进行低通滤波处理:
%% 低通滤波
fc = 20;
Wc = 2*fc/fs;
[b,a] = butter(2,Wc,'low'); % 四阶的巴特沃斯低通滤波,保留频率低于fc的振动
fprintf('a = %6.18fn',a);
fprintf('b = %6.18fn',b);
x1 = filter(b,a,x);
figure
subplot(211),plot(x1,'b'),title('低通滤波信号时域图'),xlabel('采样点/n'),ylabel('力或力矩');
fx = abs(fft(x1-mean(x1)))/(N/2); % 傅里叶变换
subplot(212),plot(f(1:Hz), fx(1:Hz),'b'),title('低通滤波信号频谱图'),xlabel('频率/Hz'),ylabel('幅值'); % 绘制原始信号频域
Butterworth digital and analog filter design:
function varargout = butter(n, Wn, varargin)
narginchk(2,4);
if coder.target('MATLAB')
[varargout{1:nargout}] = butterImpl(n,Wn,varargin{:});
else
allConst = coder.internal.isConst(n) && coder.internal.isConst(Wn);
for ii = 1:length(varargin)
allConst = allConst && coder.internal.isConst(varargin{ii});
end
if allConst && coder.internal.isCompiled
[varargout{1:nargout}] = coder.const(@feval,'butter',n,Wn,varargin{:});
else
[varargout{1:nargout}] = butterImpl(n,Wn,varargin{:});
end
end
end
function varargout = butterImpl(n,Wn,varargin)
inputArgs = cell(1,length(varargin));
if nargin > 2
[inputArgs{:}] = convertStringsToChars(varargin{:});
else
inputArgs = varargin;
end
validateattributes(n,{'numeric'},{'scalar','real','integer','positive'},'butter','N');
validateattributes(Wn,{'numeric'},{'vector','real','finite','nonempty'},'butter','Wn');
[btype,analog,~,msgobj] = iirchk(Wn,inputArgs{:});
if ~isempty(msgobj)
coder.internal.error(msgobj.Identifier,msgobj.Arguments{:});
end
% Cast to enforce precision rules
n1 = double(n(1));
coder.internal.errorIf(n1 > 500,'signal:butter:InvalidRange')
% Cast to enforce precision rules
Wn = double(Wn);
% step 1: get analog, pre-warped frequencies
fs = 2;
if ~analog
u = 2*fs*tan(pi*Wn/fs);
else
u = Wn;
end
% step 2: Get N-th order Butterworth analog lowpass prototype
[zs,ps,ks] = buttap(n1);
% Transform to state-space
[a,b,c,d] = zp2ss(zs,ps,ks);
% step 3: Transform to the desired filter
if length(Wn) == 1
% step 3a: convert to low-pass prototype estimate
Wn1 = u(1);
Bw = []; %#ok< NASGU >
% step 3b: Transform to lowpass or high pass filter of desired cutoff
% frequency
if btype == 1 % Lowpass
[ad,bd,cd,dd] = lp2lp(a,b,c,d,Wn1);
else % btype == 3 % Highpass
[ad,bd,cd,dd] = lp2hp(a,b,c,d,Wn1);
end
else % length(Wn) is 2
% step 3a: convert to low-pass prototype estimate
Bw = u(2) - u(1); % center frequency
Wn1 = sqrt(u(1)*u(2));
% step 3b: Transform to bandpass or bandstop filter of desired center
% frequency and bandwidth
if btype == 2 % Bandpass
[ad,bd,cd,dd] = lp2bp(a,b,c,d,Wn1,Bw);
else % btype == 4 % Bandstop
[ad,bd,cd,dd] = lp2bs(a,b,c,d,Wn1,Bw);
end
end
% step 4: Use Bilinear transformation to find discrete equivalent:
if ~analog
[ad,bd,cd,dd] = bilinear(ad,bd,cd,dd,fs);
end
if nargout == 4 % Outputs are in state space form
varargout{1} = ad; % A
varargout{2} = bd; % B
varargout{3} = cd; % C
varargout{4} = dd; % D
else
p = eig(ad);
[z,k] = buttzeros(btype,n1,Wn1,analog,p+0i);
if nargout == 3 % Transform to zero-pole-gain form
varargout{1} = z;
varargout{2} = p;
varargout{3} = k;
else
den = real(poly(p));
num = [zeros(1,length(p)-length(z),'like',den) k*real(poly(z))];
varargout{1} = num;
varargout{2} = den;
end
end
end
function [z,k] = buttzeros(btype,n,Wn,analog,p)
% This internal function computes the zeros and gain of the ZPK
% representation. Wn is scalar (sqrt(Wn(1)*Wn(2)) for bandpass/stop).
if analog
% for lowpass and bandpass, don't include zeros at +Inf or -Inf
switch btype
case 1 % lowpass: H(0)=1
z = zeros(0,1,'like',p);
k = Wn^n; % prod(-p) = Wn^n
case 2 % bandpass: H(1i*Wn) = 1
z = zeros(n,1,'like',p);
k = real(prod(1i*Wn-p)/(1i*Wn)^n);
case 3 % highpass: H(Inf) = 1
z = zeros(n,1,'like',p);
k = 1;
case 4 % bandstop: H(0) = 1
z = 1i*Wn*((-1).^(0:2*n-1)');
k = 1; % prod(p) = prod(z) = Wn^(2n)
otherwise
coder.internal.error('signal:iirchk:BadFilterType','high','stop','low','bandpass');
end
else
Wn = 2*atan2(Wn,4);
switch btype
case 1 % lowpass: H(1)=1
z = -ones(n,1,'like',p);
k = real(prod(1-p))/2^n;
case 2 % bandpass: H(z) = 1 for z=exp(1i*sqrt(Wn(1)*Wn(2)))
z = [ones(n,1,'like',p); -ones(n,1,'like',p)];
zWn = exp(1i*Wn);
k = real(prod(zWn-p)/prod(zWn-z));
case 3 % highpass: H(-1) = 1
z = ones(n,1,'like',p);
k = real(prod(1+p))/2^n;
case 4 % bandstop: H(1) = 1
z = exp(1i*Wn*( (-1).^(0:2*n-1)' ));
k = real(prod(1-p)/prod(1-z));
otherwise
coder.internal.error('signal:iirchk:BadFilterType','high','stop','low','bandpass');
end
end
% Note: codegen complains when z set to both real and complex values above
if ~any(imag(z))
z = real(z);
end
end
可以得到滤波后的接触力数据:

为了更详细的进行原始数据与滤波后的数据进行对比,接下来以几种不同形式的滤波方式进行对比。
原始接触力数据:

移动平均滤波
b = [1 1 1 1 1 1]/6;
x11 = filter(b,1,x);

很明显,去除噪声的效果较为突出!
接下来采用中值滤波:

中值滤波的效果相比于移动平均滤波有改善。
接下来进行维纳滤波:
Rxx=xcorr(x, x); %得到混合信号的自相关函数
M=100; %维纳滤波器阶数
for i=1:M
for j=1:M
rxx(i,j)=Rxx(abs(j-i)+N); %得到混合信号的自相关矩阵
end
end
Rxy=xcorr(x,x1); %(此处x1为中值信号滤波后效果,原信号不存在)得到混合信号和原信号的互相关函数
for i=1:M
rxy(i)=Rxy(i+N-1); %得到混合信号和原信号的互相关向量
end
h = inv(rxx)*rxy'; %得到所要涉及的wiener滤波器系数
x1=filter(h,1, x); %将输入信号通过维纳滤波器

但维纳滤波的效果没有前面两个滤波算法的效果好,需要进一步整定参数。
下面进行自适应滤波:
k=100; %时域抽头LMS算法滤波器阶数
u=0.001; %步长因子
%设置初值
x1=zeros(1,N); %output signal
x1(1:k)=x(1:k); %将输入信号SignalAddNoise的前k个值作为输出yn_1的前k个值
w=zeros(1,k); %设置抽头加权初值
e=zeros(1,N); %误差信号
%用LMS算法迭代滤波
for i=(k+1):N
XN=x((i-k+1):(i));
XN=XN';
x1(i)=w*XN';
e(i)=x11(i)-x1(i);%不存在原信号,此处换为平均滤波后的时域波形
w=w+2*u*e(i)*XN;
end

四阶的巴特沃斯低通滤波:
Wc=2*3/fs; %截止频率 3Hz
[b,a]=butter(4,Wc,'low'); % 四阶的巴特沃斯低通滤波
x1=filter(b,a,x);

二阶的巴特沃斯带通滤波:
Wc1=2*1/fs; %下截止频率 1Hz
Wc2=2*6/fs; %上截止频率 6Hz
[b,a]=butter(2,[Wc1, Wc2],'bandpass'); % 二阶的巴特沃斯带通滤波
x1=filter(b,a,x);

需要生成滤波器时,可以使用matlab中自带的工具。filterDesigner
利用这个工具,可以将设计的滤波器保存成一个函数。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
接触力对120A250A大电流接线端子有哪些影响2024-07-09 1050
-
柔性触觉传感器或将在人形机器人时代大放异彩2023-12-13 1783
-
机器臂柔顺控制初步分析2023-11-22 1125
-
力控机器人接触力滤波与估计2023-11-10 1068
-
机器人力控的性能指标有哪些2023-11-08 1808
-
机器人接触式物体探测的接触方式有哪些?2020-03-02 2234
-
机器人基础书籍2019-05-22 3546
-
机器人的眼睛和大脑:智能化光电传感器2018-11-06 2656
-
机器人、协作机器人和移动机器人,你分的清楚吗2018-10-30 3987
-
软固结磨粒群接触力分析2018-03-16 900
-
机器人弹钢琴,实现难度如何?2017-05-22 6167
-
nao机器人与其他机器人的区别2015-02-13 6830
全部0条评论

快来发表一下你的评论吧 !

