

工业现场相机坐标系和机械手坐标系的标定
描述
工业现场使用视觉时一般需要相机坐标系和机械手臂坐标系的转化,这里介绍一种比较简单的标定方案。没有使用到标定板。经过几个项目的测试,精度还算可以,如果要求高精度的场合,就用标定板标定吧!【可以购买专用的标定板,或者自己制作(像我这种穷逼),哈哈
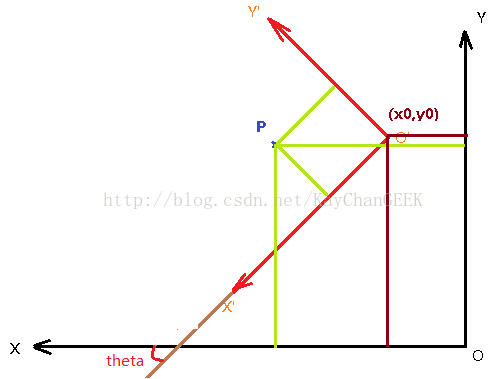
如上图所示:OXY为机械手坐标系,O'X'Y'为相机坐标系。theta为两个坐标系之间的夹角。假设P点在图像上的位置如图,则P在机械手坐标系有一个坐标,在图像坐标系也有一个坐标。我们要做的工作就是图像上的任意一点都可以转化为机械手坐标系上的坐标点:P(Machine) = f(P(Image))。接下来介绍如何找到这个关系。
OXY为机械手坐标系 O'X'Y'为相机坐标系从上图可以看出坐标转化关系:
x = x' * r * cos(theta) - y' * r * sin(theta) + x0;
y = x' * r * sin(theta) + y' * r * cos(theta) + y0;
其中r是毫米像素比、(mm/pixel)就是一个毫米有几个像素,theta为两个坐标系之间的夹角,(x0,y0)为图像坐标原点到机械坐标原点的距离。
简化抽象公式,假设:
a = r * cos(theta);
b = r * sin(theta);
c = x0;
d = y0;
得到:
x = x' * a - y' * b + c;
y = x' * b + y' * a + d;
很显然,要解出这个方程,需要两组对应关系,就是两组对应的坐标点。设两组坐标点,如下:
第一组:图像坐标点:(xImage1,yImage1) 对应的机械坐标点:(xMachine1,yMachine1)
第二组:图像坐标点:(xImage2,yImage2) 对应的机械坐标点:(xMachine2,yMachine2)
则可以解出a ,b, c, d。如下:
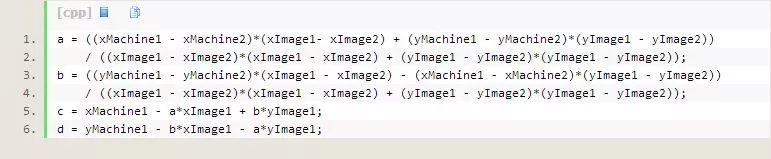
所以,就得出了图像上任意一点的像素坐标转成机械手坐标的关系。
以下是我写的一个求解a ,b, c, d软件:
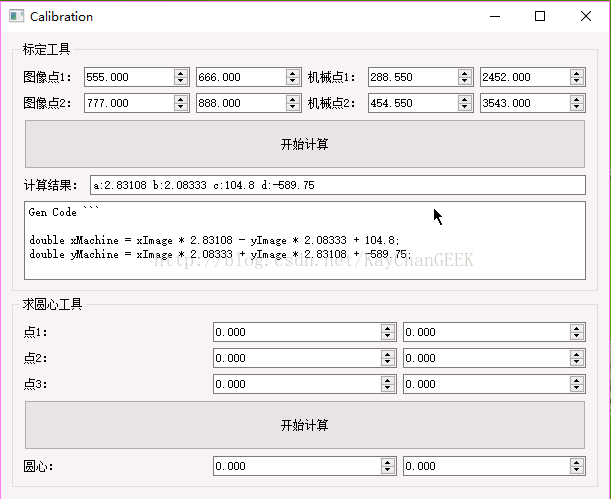
下面举个栗子说明一下操作吧!这是我实际项目中的机械手和相机布局情况,画图真T``M`累!,如下图:
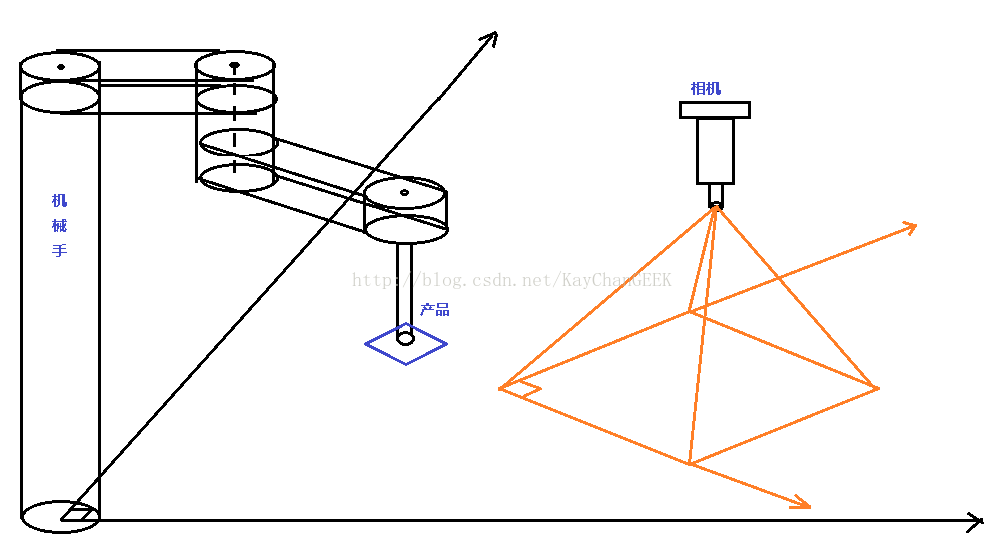
首先将产品上的目标点搞到机械手的Z轴的中心,然后移动到相机视野范围内,让识别产品上的目标点,这时,你会读到一组机械手坐标(也就是上面所说的(xMachine1,yMachine1)),和一组相机坐标(也就是上面所说的(xImage1,yImage1)),再在相机视野范围内移动机械手,就可以得到第二组数据(xMachine2,yMachine2)和(xImage2,yImage2),写入标定软件就可以求出a, b, c, d。就求出了图像上任意一点对应的机械坐标,然后你下次移动第二个产品到相机视野时,首先识别目标点的像素坐标,经过对应的转换就可以得出机械坐标,然后进行相应的偏移即可实现你想要的操作!
当然,有些时候,实际现场并没有如你所愿,现在出现一种情况就是以机械手自带的Z轴无法移动到视野中去,这样就无法进行上面的操作了,系不系!这也是我遇到的情况,SO,我的解决方案如下:先上示意图:
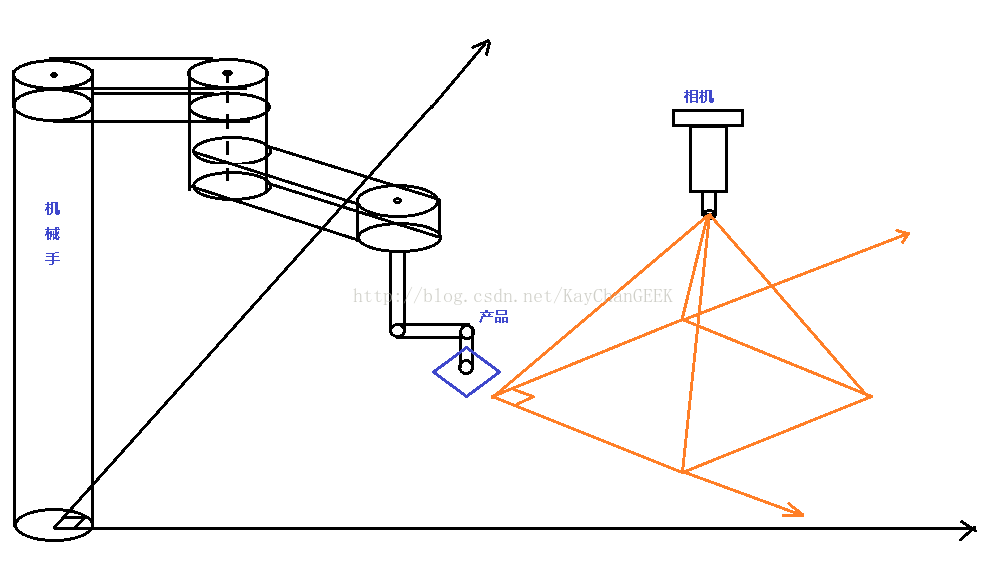
如图,就是在机械手Z轴的横杆上加上一个横条,使得产品可以移动到视野范围内。然后进行上面的操作,虽然现在可以将产品移动到视野范围内了,但是你会发现此时机械手的坐标并不是产品的坐标,因为他们之间隔着一个横条,那我们要怎么换算过来呢!
首先,我们可以这么假定的认为,他们是机械手的坐标就是产品的坐标,然后就可以用上面取两组对应点的方法求出图像上每个点的机械坐标了,但是,此时的机械坐标并不是真正的机械坐标,但是,我们可以利用这些坐标找出机械手U轴的旋转中心就是Z轴(就是实际机械坐标所在的位置)在我们所建立的不是真正的机械坐标系中的坐标。是不是有点不好理解,我也不大清楚怎么描述!求U轴的旋转中心的过程如下:上图:
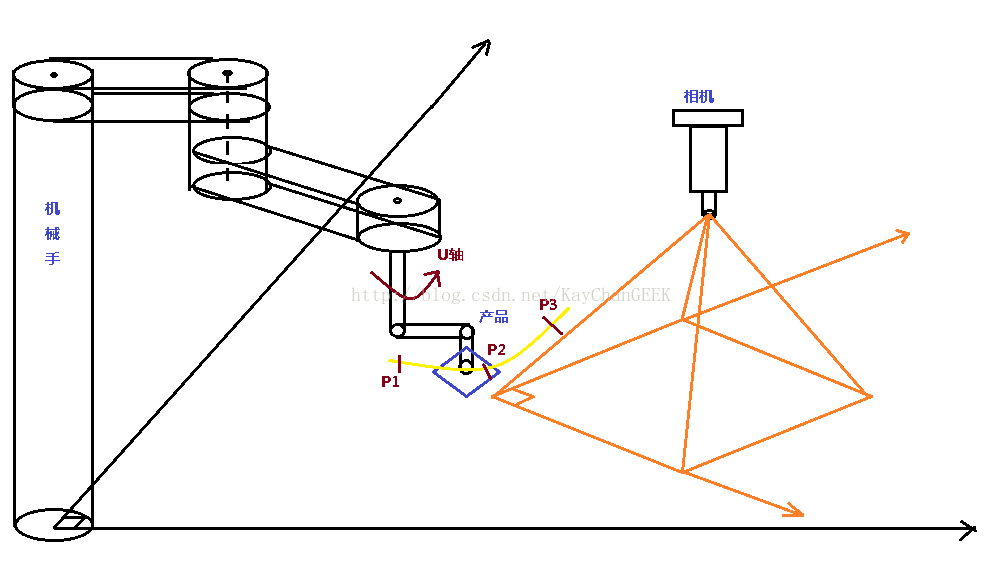
如图:将产品的目标点绕机械手的U轴的旋转中心旋转得到3的目标点的不是真正的机械坐标系的坐标P1,P2,P3,必须让每次旋转的目标点在视野范围内,然后通过圆弧上的3点就可以求得圆心。此时的圆心坐标为不是真正的机械坐标系的坐标。然后我们就可以求出产品中心和机械手U轴旋转中心的deltaX,deltaY,然后就可以结合真正的机械坐标系建立工件坐标系,要对机械手有些了解才比较好理解这些拗口的话!然后对于每一个新的产品都可以建立合适的工件坐标系,然后进行补正和一些操作!
相机跟随着机械手运动(它们绑定在一起了),如果还将标定靶标也固定在机械手上的话,三个对象都相对运动,就无法标定了!那要怎么利用标定助手完成标定呢?经过思考,我给出了以下标定思路:
整个标定系统的初始状态
相机和机械手绑定在一起并且机械手旋转中心处于机械原点,这时候相机中心和机械手中心有一个相对的偏移并且是固定的(相机中心和机械手旋转中心的相对距离设为(detX,detY)),将标定靶标放置在工作区域(实际机械手的工作区域)中的合适位置。
第一步:求取第一组图像点坐标C1
移动机械手(相机会跟着移动)到相机能够清晰拍摄到标定靶标的位置(设该位置的机械坐标为(x0,y0))。然后调整标定靶标的识别参数,使得能够实时的识别标定靶标的中心位置,手动移动靶标最好让它远离图像中心,越远越好(精度越高)但是不能超出相机的视野范围,我就把靶标放在相机视野的左上角的区域吧,然后我们识别当前靶标的图像位置C1,就是第一组数据的图像点。
第二步:求取第一组机械点坐标M1
进入“标定”选项卡,勾选“显示十字标”,这时候会在实时图像中间显示一个蓝色的十字光标,然后,慢速移动机械手,直到C1点和十字光标的交点重合(也就是说移动机械手让实时识别到的靶标中心坐标处于图像的中心,比如采集的图像为2048*1536大小的,你需要缓慢移动机械手(靶标保持不动)直到靶标的中心处于(1024,768)的这个位置),然后记下当前的机械手坐标也就是第一组数据的机械点M1(注意:此时实际是让相机中心和靶标中心重合,并非机械手旋转中心和靶标中心重合,它们之间差了一个detX,detY的距离,具体怎么换算,等下再说)。
第三步:求取第二组图像点坐标C2
将机械手移动回到初始的工作坐标点(x0,y0),将靶标放在相机视野的右下角的区域,识别当前的靶标图像坐标C2,就是第二组数据的图像点。
第四步:求取第二组机械点坐标M2
同理,慢速移动机械手,直到C2点和十字光标的交点重合(就是移动机械手让实时识别到的靶标中心坐标处于图像的中心),然后记下当前的机械手坐标也就是第二组数据的机械点M2。
第五步:求取整个机械手工作区域坐标系和相机坐标系的对应关系
不知道你有没有发现,上面求得工作区域只对工作区域(x0,y0)开始到相机视野结束的位置有效(比如你在机械手移动到工作区域(x0,y0)为起点的位置识别靶标的图像位置坐标为(100,100),但是你将机械手移动到工作区域(x1,y1)为起点的位置识别靶标的图像位置坐标也可能为(100,100))。这样换算过来的机械坐标就是错误的,其实我们上面求得是小区域的转换关系,那我们要怎么扩展到整个机械手的工作区域呢?我们只需要这样做:在机械手工作的时候是可以知道自己在哪里的,比如:现在机械手移动到工作区域(x1,y1)为起点的位置识别靶标的图像位置坐标为(100,100),我们将(100,100)代入转换关系trans得出来的机械坐标是对应(x0,y0)的,要转换到对应(x1,y1)的只需要将换算处理的坐标加上(x1 - x0,y1 - y0)即可!抽象的公式如下:

其中trans函数就是将图像坐标转换为相对于(x0,y0)工作区域的机械坐标,再加上坐标(x1 - x0,y1 - y0)就是当前正确的机械坐标。到此,我们得到了图像坐标和整个机械手工作区域的坐标的关系,但是此时的机械坐标指的是相机的中心,并不是机械手的旋转中心。
第六步:将相机中心转换为机械手的旋转中心
首先,你可以利用目测法,游标卡尺法等等粗略的算出detX,detY的值,然后,进行实时识别和移动测试进行细调,因为粗略的估算有误差,你可以经过多次微调直到精确到机械手的旋转中心移动到产品的上方就成功了。记下此时的detX,detY,代入以下公式就可以算出了最终的机械手应该去的地方了。最终的换算公式如下:

整个过程的伪代码运算过程如下:
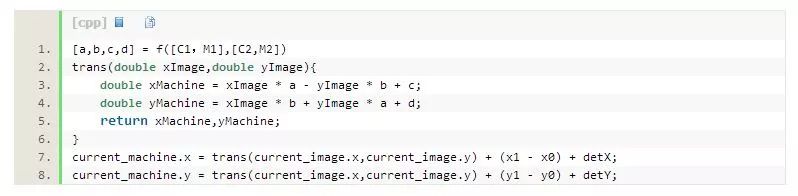
利用标定助手求取[a,b,c,d]外参矩阵的输入参数[C1,M1]和[C2,M2]的操作方法如下图所示:
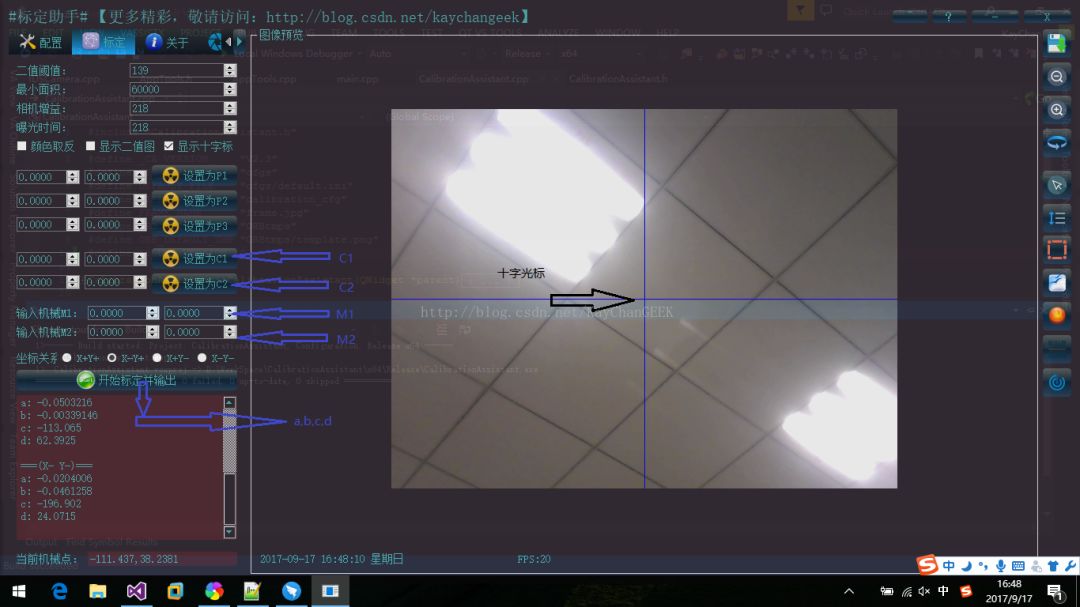
-
MATLAB建立和控制图形窗口和坐标系命令2009-09-22 11529
-
坐标系转换与手眼标定2019-06-20 2352
-
解决电压方程在静止坐标系与运动坐标系转换问题2021-08-27 1565
-
什么是坐标系2009-12-31 5005
-
坐标系与鱼雷运动参数2010-01-06 5906
-
机器人基坐标系标定方法研究2018-03-07 994
-
OPENGL坐标系介绍 世界坐标系和当前绘图坐标系区别2018-05-04 13163
-
带你来剖析机器人的坐标系吧!2020-05-09 5833
-
介绍一种比较简单的工业现场相机坐标系和机械手坐标系的标定方案2022-09-05 2521
-
相机标定之四个坐标系之间的变换关系2023-03-08 5340
-
自动驾驶各个坐标系2023-06-01 591
-
三坐标如何建立坐标系?2023-02-17 13260
-
世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的关系2023-07-03 15187
-
深度剖析机器人的四大坐标系2023-11-13 2961
-
应用卫星通信领域的一个坐标转换过程—机体坐标系与ENU坐标系的转换2023-12-27 7707
全部0条评论

快来发表一下你的评论吧 !

