

OTFS调制和解调详解
描述
以下内容为4.1节“系统模型”的中文翻译,原文请参考英文版《Delay-Doppler Communications Principles and Applications》一书,若本文中存在翻译错误或者编辑错误,欢迎留言指正。
随着高速列车、无人机、无人驾驶汽车的出现,高移动性无线信道迫切需要可靠的通信。在OFDM中,信息符号在单个时频资源上传输,容易受到频率和时间选择性衰落的影响,从而降低了高可移性无线信道中的错误性能。另一方面,OTFS在一个跨越整个时间和频率资源的二维(2D)正交基函数上复用每个信息符号。因此,所有信息符号都经历一个固定的(时不变的)平坦衰落等效信道。
本章从离散时域、时频域和延迟-多普勒域等不同域的一些基本符号开始,然后描述OTFS调制和解调、高移动率信道以及OTFS与理想脉冲成形波形的输入输出关系。
在本章的后面,我们将介绍OTFS矩阵形式,展示OTFS调制如何与众所周知的离散Zak变换相关。然后,我们用实际矩形脉冲成形波形给出OTFS的输入输出关系的矢量化形式,其中考虑了不同的域:离散时域、时频域、延时时域和延时多普勒域。进一步,我们将我们的研究扩展到OTFS的变体,在这些波形的传输中,每个OTFS帧或块添加一个循环前缀(CP)或零填充(ZP)。最后,我们对OTFS变体的信道表示和输入输出关系进行了全面的总结。
4.1系统模型
在本节中,在描述图4.1中OTFS调制和解调模块之前,我们介绍有关三个领域的一些符号:离散时域、时频域和时延-多普勒域。
我们假设OTFS系统运行在一个带宽为B、最大时延扩展和最大多普勒频移的P条路径信道上,定义为(2.11)。我们考虑一个离散时间基带等效模型,其中连续时间OTFS信号以采样频率进行采样,其中Ts表示采样间隔。离散域OTFS帧包含了被细分为N个块(或时隙)的NM样本,每个块有M个样本。因此,OTFS帧持续时间为,其中表示每个块的持续时间。
每T秒内,获得每个块M点DFT的离散频谱,频点间隔∆f=1/T。带宽B=M∆f的OTFS帧的所有N块时间轴称为时频域,如图4.2(左)所示,离散时频域定义为MN点阵列
M,N>0。在Λ的点集合中离散时频样本矩阵表示为。其中每一列包含每个块的离散频谱样本。将这个矩阵看作一维时域OTFS信号的二维时频表示是很方便的。
离散时频样本可以通过二维辛傅里叶变换转换到延迟-多普勒域。具体来说,延时-多普勒域是通过沿频率轴(列)和沿时间轴(行)的傅里叶反变换从时频域得到的。离散后,在时延-多普勒域对应的MN点阵列(图4.2(右))为
其中,1/MΔf和1/NT分别为路径延迟和多普勒频移的分辨率。特别是具有相同多普勒频移但传播延迟小于1/MΔf不同的两条路径,接收机无法区分。同样,具有相同传播延迟但多普勒频移差小于1/NT的两条路径也无法区分。
我们定义OTFS波形Γ点的延迟-多普勒采样为矩阵。
4.1.1 OTFS系统的参数选择
作为设计的重要参数,我们选择。我们知道T和∆f决定了可支持的最大信道时延 和多普勒频移 。如果固定数据率到每帧NM个符号,根据信道参数,我们可以选择T越大(∆f越小),将得到越小的N和越大的M,反之亦然。这意味着OTFS可以处理最大,扩展了设计工作在低度扩展信道之外的系统的机会()。OTFS系统的另一个设计约束在于假设多径信道参数(见第2章)在帧的持续时间内是恒定的。在今天的蜂窝系统环境中,这将T_f限制在最大10 ~ 20毫秒。
4.1.2 OTFS调制
正如图4.1所示,在发射端,经调制后的长度为Q的序列构成NM信息符号,放置到时延-多普勒域矩阵,并且。
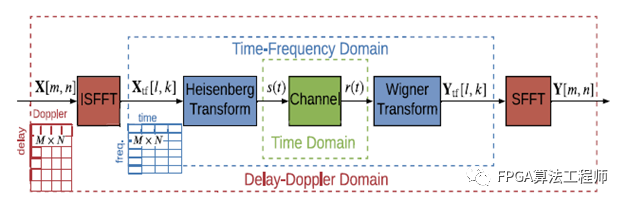
图4.1 原始形式的OTFS系统图
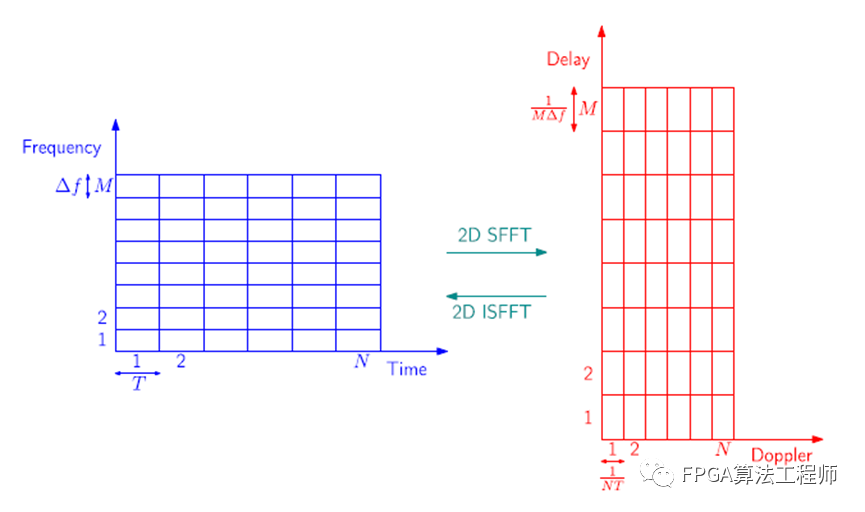
图4.2 离散时频网格(Λ)和时延-多普勒网格(Γ)
发射机首先通过逆辛-傅里叶变换(ISFFT)将符号映射到NM样本的时频资源格Λ:
,表示时频域发射样本矩阵。ISFFT对应于一个二维变换,取X列的m点进行DFT和X行的n点进行逆DFT (IDFT)。接下来,时频调制器用发射波形对2D的转换为连续时间波形s(t):
上述操作在文献中称为海森堡变换,它依赖于。
4.1.3 高速移动信道失真
信号通过时延-多普勒信道响应h(τ,ν)传输,对应于时延响应g(τ,t),其中τ,ν是信道时延和多普勒频移(参见第2章)。忽略噪声项,接收信号r(t)由下式给出:
其中,在(2.15)式已给出。
在接收机中,信道受损信号r(t)被离散采样,。则(4.4)变为
其中,是在时偏的多普勒响应。集合包含信道不同的时偏, 是所有具有相同时偏 的路径的多普勒频移的集合。
现在我们考虑一个由P条路径组成的时变多径信道,第条路径()有信道增益,时延,多普勒频移,在时延的多普勒响应为:
特别地,当归一化的时延和归一化的多普勒频移是整数时,我们用(整数时延抽头)和(整数多普勒抽头)表示。然后将(4.6)中的sinc函数替换为(处的单位脉冲,得到离散的延迟时间多径信道响应:
第二步是由于(4.7)。假设的最大值小于最大信道延迟抽头,其中。
这里需要注意的是,假设延迟多普勒(或等效的延迟时间)响应在一个OTFS帧的持续时间内是固定的。这意味着,假设的时延-多普勒信道参数是恒定的。为了满足这一假设,可能有必要以降低多普勒频移分辨率为代价降低N。
4.1.4 OTFS解调
在图4.1中,在接收端,接收到的信号r(t)通过一个匹配滤波器,计算交叉模糊函数为
然后在网格点Λ上对进行采样,形成带条目的时频域接收样本矩阵。
,(4.9)和(4.10)合起来称为维格纳变换。最后,对进行辛快速傅里叶变换(SFFT),得到的时延-多普勒域样本为:
SFFT对应于一个二维变换,它对Y的列进行m点的IDFT,再对Y的行进行n点的DFT。综上所述,如图4.1所示,OTFS调制器利用ISFFT将时延-多普勒域的映射到时频域的。然后对进行海森堡变换,得到时域信号。在接收端,通过Wigner变换变换到时频域,然后使用SFFT变换到延迟-多普勒域,然后进行符号解调。
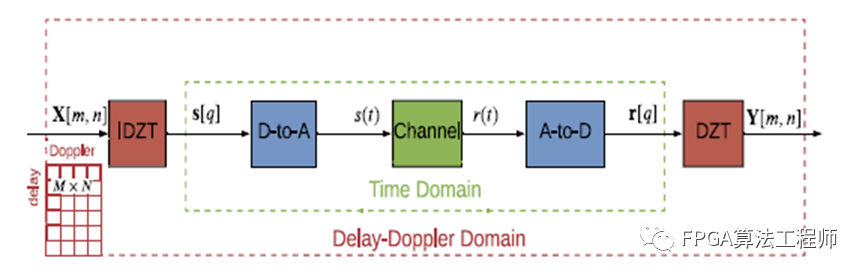
图4.3 OTFS系统图使用离散Zak变换
或者,OTFS发射机可以使用逆离散Zak变换(IDZT)和数模转换器(DA)来实现,以形成发射信号s(t),如图4.3所示。OTFS接收机可以在接收信号r(t)中使用模数转换器(AD),然后使用离散Zak变换(DZT)来实现。这种等价性将在第4.3节中变得明显,我们请读者参阅第5章以了解关于Zak变换的详细信息。
审核编辑:汤梓红
-
有关于π/4DQPSK调制解调端仿真的吗???2012-03-05 2758
-
基于labview的模拟调制解调设计2015-12-09 3468
-
labview调制与解调2016-05-07 3870
-
调制器和解调器2017-12-07 4235
-
调制器和解调器的测试手段和测试方法2019-07-19 2583
-
基于simulink频率调制和解调仿真咋做2020-02-14 9024
-
Multisim调制解调电路仿真2020-04-14 5873
-
关于QPSK及OQPSK信号的调制和解调方法2021-04-28 5810
-
求一种基于VHDL的4PSK信号的调制和解调设计方案2021-04-30 1580
-
如何用FX489实现GMSK信号的调制和解调?2021-06-07 1877
-
调制与解调2008-09-24 6748
-
锁相环在调制和解调中的应用2012-09-21 4561
-
浅谈调制解调器2023-05-25 2578
-
OTFS调制技术的基本原理和优缺点2023-09-19 19415
-
ofdm调制和解调过程2023-12-25 5153
全部0条评论

快来发表一下你的评论吧 !

