如何权衡阻抗控制性能与稳定性的关系

阻抗控制性能提升后对稳定性有怎样的影响？如何权衡阻抗控制性能与稳定性的关系？

当阻抗控制性能提升时，往往需要更高的控制增益来实现更快的响应和更小的跟踪误差。

这会导致控制系统的稳定性受到挑战，因为高增益会导致系统出现振荡或不稳定的情况。因此，需要在性能和稳定性之间进行权衡。

一般来说，权衡性能和稳定性的最好方法是通过系统的频率响应特性进行分析。在频率域中，系统的增益和相位可以得到明确的量化，因此可以根据实际要求对控制增益进行优化。

此外，也可以使用一些经典的控制方法，如根轨迹设计或Bode图设计，来平衡性能和稳定性。最终，选择合适的方法取决于具体应用场景和系统要求。

阻抗控制一般可以通过一些实验进行验证，例如实验涉及阻抗控制的两个典型应用领域：机器人与人的稳定和安全交互，以及与未知、刚性但被动环境的接触。

要求机器人对与刚体动力学、有效载荷或接触环境相关的模型不确定性具有鲁棒性。增强控制方法的鲁棒性、性能和通用性。通过输入变量与输出变量之间的关系来衡量性能。

虽然交互性能的测量可能随着系统和任务的不同而变化，但它们最好由控制机器人的行为决定。当机器人被期望管理与几个不同或不确定性的环境的交互时，根据耦合系统的行为来指定性能（例如，固有频率、阻尼）可能是不切实际的。

机械阻抗是衡量结构在(谐波)力作用下抵抗运动的程度。阻抗的倒数是导纳。它是速度与力的比值。你可以想象用一定的频率推孩子的秋千。

摆动的导纳越低，达到相同的摆动速度所需的力就越大。一个有很高导纳的秋千只需要轻轻推一下，孩子就会荡到天上。

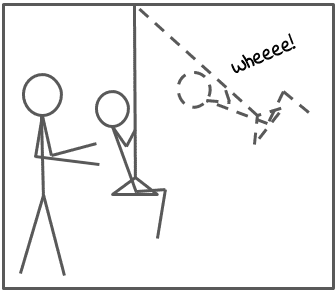
当你用一定的力击打重袋子(纯质量)时，加速度与袋子的质量成正比。

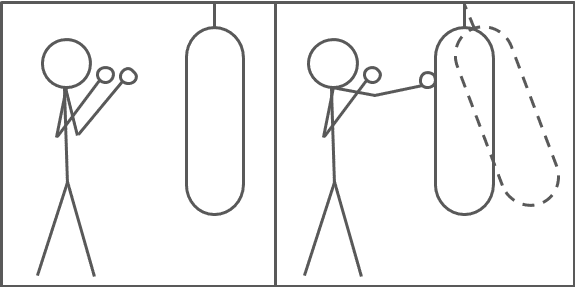
假设袋子像弹簧一样运动，当你用一定的力击打袋子时，袋子表面的位移将与袋子材料的刚度成正比，直到拳头的力和弹簧的力达到平衡。

水里面打拳，则效果图下图所示

阻尼力与速度成正比！

通过控制阻抗，通过定义其刚度和阻尼来控制机器人在与环境交互过程中的行为。可以让它表现得像一个非常松散的弹簧，具有很高的顺应性!

当机器人被推时，它会向后移动，直到一段时间后到达它的初始位置。如果我们增加一些阻尼，末端执行器甚至可能在位移后回到它的初始位置，没有任何振荡。相反，机器人只会移动，如果环境中有很大的力，如果刚度很高。

在位置控制中，命令一个特定的位置，机器人无论如何都要到达该位置。如果它不能很容易地到达位置，它会施加很高的力，这可能会造成损坏。

如果使用阻抗控制，可以间接控制力，从而避免这种破坏性的高力。如果有一些不确定因素，例如，钻孔稍微错位，这是特别好的。机器人会做出顺从的动作，也就是说，它会对接触做出轻微的反应。

如果机器人的末端执行器没有与另一个物体接触，力控制就会表现得很差，因为力会导致快速运动。想想爬楼梯，错误地认为最后还有一个台阶。

抬起脚，试着推到台阶上。因为没有建立联系，能量就会流失，必须努力保持平衡。

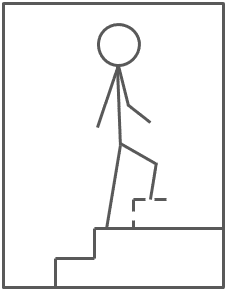
以下是一个简单的单自由度机器人阻抗控制的 MATLAB 程序示例，其中机器人的动力学模型是简化为一个弹簧阻尼系统：

% 机器人阻抗控制程序


% 机器人参数
m = 1;          % 质量
k = 10;         % 刚度
c = 1;          % 阻尼


% 阻抗控制参数
Kp = 20;        % 位置控制增益
Kv = 5;         % 速度控制增益
M = 5;          % 质量控制增益
B = 1;          % 阻尼控制增益


% 目标参考位置和力/力矩
qr = 1;         % 参考位置
fr = 0.1;       % 参考力/力矩


% 初始状态
x0 = [0; 0];    % 位置和速度
f0 = 0;         % 初始力/力矩


% 阻抗控制循环
t = 0:0.01:10;  % 时间向量
x = zeros(2, length(t));     % 位置和速度
f = zeros(1, length(t));     % 力/力矩
x(:,1) = x0;    % 初始状态
f(1) = f0;


for i = 2:length(t)
    % 计算误差和误差导数
    e = qr - x(1, i-1);     % 位置误差
    de = -x(2, i-1);        % 速度误差
    
    % 计算控制力/力矩
    fc = Kp*e + Kv*de + M*(fr-f(1)) + B*(-x(2,i-1));
    
    % 更新状态
    a = (fc - c*x(2,i-1) - k*x(1,i-1))/m;
    x(2,i) = x(2,i-1) + a*0.01;
    x(1,i) = x(1,i-1) + x(2,i)*0.01;
    
    % 记录控制力/力矩和位置
    f(i) = fc;
end


% 绘图
subplot(2,1,1)
plot(t, x(1,:), 'b', t, qr*ones(size(t)), 'r--')
xlabel('时间 (s)')
ylabel('位置 (m)')
legend('位置', '参考位置')
title('单自由度机器人阻抗控制')


subplot(2,1,2)
plot(t, f, 'b', t, fr*ones(size(t)), 'r--')
xlabel('时间 (s)')
ylabel('力/力矩 (N/m)')
legend('控制力/力矩', '参考力/力矩')

结果如下：

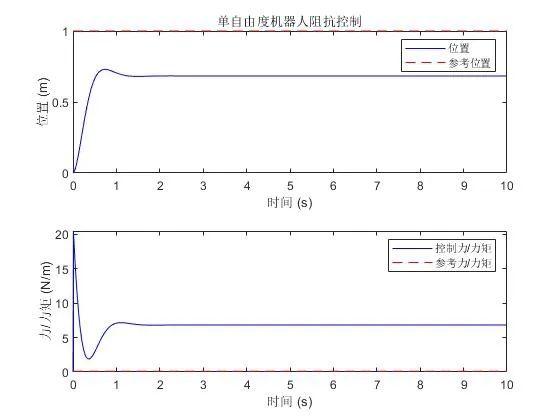
根据程序运行的结果和可视化图形可以看出，阻抗控制使得机器人的末端可以按照期望的阻抗响应，即在受到外界干扰时具有一定的柔性和减震性能，从而实现了对外部力的主动响应。

通过调节阻抗控制器中的参数，可以使机器人末端的运动更加平滑和稳定。此外，对于单自由度机器人来说，阻抗控制器在保证稳定性的同时还能够提高系统的动态性能，使得机器人在对外界干扰响应时的响应速度更快，具有更好的跟踪性能。

然而，阻抗控制器中的参数调节比较困难，需要根据实际情况进行经验性调整，同时阻抗控制器也容易出现过冲和振荡等问题，因此需要综合考虑性能与稳定性之间的权衡关系，进行合理的参数设计。