OpenCV图像处理之图像梯度+Canny边缘检测

 

1. 图像梯度

 

首先我们来看看什么是图像梯度：图像梯度可以把图像看作二维离散函数，图像梯度就是这个二维函数的求导，图像边缘一般都是通过对图像进行梯度运算来实现的

在图像梯度这一部分我们会接触查找图像梯度、边缘等，这一部分涉及了三个主要函数：cv.Sobel()，cv.Scharr()，cv.Laplacian()，相对应的，OpenCV提供的三种类型的梯度滤波器（高通滤波器），即Sobel、Scharr和Laplacian

在上一部分2D卷积即图像过滤内容中我们说了低通滤波器（LPF）与高通滤波器（HPF）的主要应用方向，LPF用于消除噪声，HPF用于找到边缘，在图像梯度这一部分我们使用三个高通滤波器来找到图像中的边缘

1.1 Sobel和Scharr算子

Sobel算子是高斯平滑与微分操作的结合体，所以其抗噪声能力很好，我们可以设定求导方向（xorder或yorder），还可以设定使用的卷积核大小ksize

当我们设定的卷积核的大小为-1时，会默认使用3x3的Scharr滤波器，它的效果比3x3的Sobel效果更好，并且处理速度相同，所以在使用3x3Sobel滤波器时应使用Scharr滤波器代替

从上面所说的概念我们可以理解为：使用3x3内核的Sobel滤波器并不等于Scharr滤波器，但Scharr滤波器是一种3x3内核的高效滤波器，若我们需要3x3内核的Sobel滤波器，那我们建议使用Scharr滤波器，即在使用Sobel滤波器时设定其内核大小为-1

了解了Sobel和Scharr高通滤波器的内核，我们再来看看cv.Sobel()和cv.Scharr()函数的参数，cv.Sobel(img,cv.CV_64F,dx,dy,ksize)函数需要传递的参数分别是原图像，cv.CV_64F是图像深度，一般写作-1就可以了，dx和dy分别表示x轴方向和y轴方向的算子，ksize就是内核

而Scharr高通滤波器是3x3的内核，所以cv.Scharr()的参数与cv.Sobel()函数对比少传递一个ksize参数即可

1.2 Laplacian算子

Laplace其实利用Sobel算子的运算，它通过Sobel算子运算出图像在x方向和y方向的导数，得出拉普拉斯变换结果，它就像Sobel算子的升级版

下面我们上俩例子方便大家理解

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread(r'E:image	est06.png', 0)
laplacian = cv.Laplacian(img, cv.CV_64F)
sobelx = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=5)
sobely = cv.Sobel(img, cv.CV_64F, 0, 1, ksize=5)
plt.subplot(2, 2, 1), plt.imshow(img, cmap='gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 2), plt.imshow(laplacian, cmap='gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 3), plt.imshow(sobelx, cmap='gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(2, 2, 4), plt.imshow(sobely, cmap='gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])
plt.show()

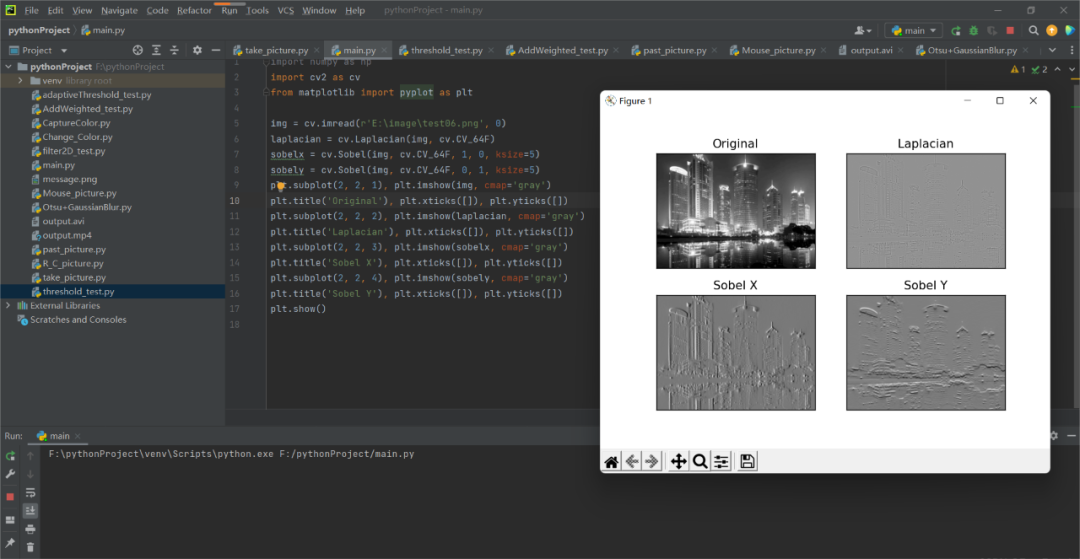
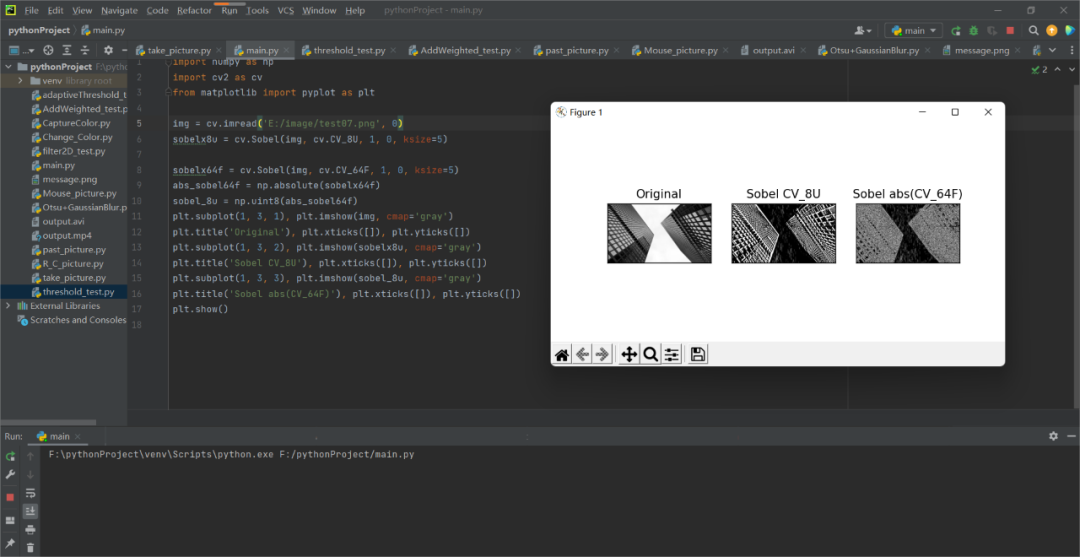
注意：在上面的实例中，输出的数据类型为cv.CV_8U或np.uint8，问题就出在这里，黑色到白色的过渡被视为正斜率（具有正值），而白色到黑色的过渡被视为负斜率（具有负值），当我们将数据转换为np.uint8时，所有负斜率均设为零，意思就是我们会错过这一边缘信息

当要检测两个边缘，更好的选择是将输出数据类型保留为更高的形式，取其绝对值然后再转回cv.CV_8U

这是一个必较重要且不容忽略的问题，所以我们再通过一个例子来看看

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('E:/image/test07.png', 0)
sobelx8u = cv.Sobel(img, cv.CV_8U, 1, 0, ksize=5)

sobelx64f = cv.Sobel(img, cv.CV_64F, 1, 0, ksize=5)
abs_sobel64f = np.absolute(sobelx64f)
sobel_8u = np.uint8(abs_sobel64f)
plt.subplot(1, 3, 1), plt.imshow(img, cmap='gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 2), plt.imshow(sobelx8u, cmap='gray')
plt.title('Sobel CV_8U'), plt.xticks([]), plt.yticks([])
plt.subplot(1, 3, 3), plt.imshow(sobel_8u, cmap='gray')
plt.title('Sobel abs(CV_64F)'), plt.xticks([]), plt.yticks([])
plt.show()

2. Canny边缘检测

 

Canny Edge Detection是由John F. Canny发明的一种流行的边缘检测算法，这是一个多阶段，主要分为：高斯滤波、梯度计算、非极大值抑制和双阈值检测

2.1 多阶段的Canny边缘检测算法

高斯滤波（降噪）

由于边缘检测很容易收到图像中噪声的影响，因此我们通过Canny边缘检测算法进行图像处理时第一步是使用5x5高斯滤波器消除图像中的噪声

高斯滤波的具体方法是生成一个高斯模板，使用卷积进行时进行时域滤波

梯度计算

使用Sobel核在水平和垂直方向上对平滑图像进行滤波，以在水平和垂直方向得到一阶导数

非极大值抑制

在获得梯度大小和方向后，将对图像进行全面扫描，以去除可能不构成边缘的所有不需要的像素，为此在每个像素处检查像素是都是在其梯度方向上附近的局部最大值

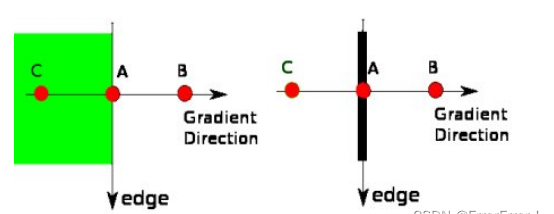
点A在边缘（垂直方向）上。渐变方向垂直于边缘。点B和C在梯度方向上。因此，将A点与B点和C点进行检查，看是否形成局部最大值。如果是这样，则考虑将其用于下一阶段，否则将其抑制（置为零）。简而言之，你得到的结果是带有“细边”的二进制图像

磁滞阈值（双阈值检测）

在这个阶段会确定哪些边缘是真正的边缘，为此我们需要提供两个阈值minVal和maxVal，强度梯度大于maxVal的任何边缘必定是边缘，而小于minVal的任何边缘必定不是边缘，如果讲他们连接到边缘像素。则将他们视为边缘的一部分否则将被丢弃

边缘A在maxVal上，因此被视为“确定边缘”，尽管C低于minVal但它连接到A，因此被视为有效便，我们得到了完整的曲线

但是尽管B在minVal上并且与C处于统一区域，但是它没有连接到任何确保边缘，因此它也会丢弃

注意：我们必须选择相应的minVal和maxVal才能获取正确的结果

2.2 OpenCV中的Canny Edge检测

OpenCV将Canny边缘检测算法的四个阶段放在了一个单数cv.Canny()中，我们只需要去正确使用它就能获取我们的边缘检测需求

我们看看cv.Canny()这个函数的传参，第一个参数是图像资源，第二、三个参数分别是用于磁滞阈值（双阈值检测）阶段的两个阈值minVal和maxVal，第四个参数是picture_size，它用于查找图像渐变的Sobel内核的大小，默认为3，第五个参数是L2gradient，它指定用于查找梯度的方程式，若为True会使用更精确的公式，若为False则用默认

我们通过一个例子来看看

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread('E:/image/test08.png', 0)
edges = cv.Canny(img, 100, 200)
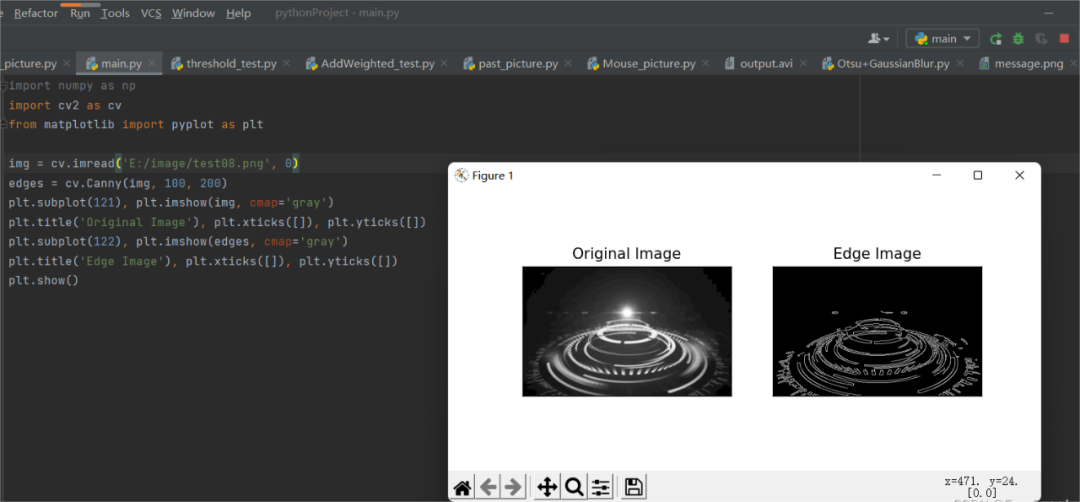
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(edges, cmap='gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])
plt.show()

 

 

 

3. 图像金字塔

 

3.1 金字塔理论基础

在之前我们学习的内容中，使用的都是像素大小恒定不变的图像，但是在一些情况下，我们在处理图像时不知道我们所需要的物体的具体尺寸（或物体是以什么样的尺寸出现在图像中）

在这种情况下我们需要创建一组具有不同分辨率的相同图像，并在这些图像中搜索目标对象，这些具有不同像素大小的图像集就是我们的图像金字塔

因为当它们堆叠在底部时，最高分辨率的图像位于顶部，最低分辨率的图像位于顶部时，看起来像金字塔

一般来说有两种金字塔：高斯金字塔和拉普拉斯金字塔

3.1.1 高斯金字塔

高斯金字塔中的较高级别（低分辨率）是通过先用高斯核对图像进行卷积再删除偶数行和列，然后较高级别的每个像素由基础级别的5个像素的贡献与高斯权重形成，通过这样的操作M x N的图像变为M/2 x N/2图像,因此面积减少到原来的四分之一，我们称之为Octave，当我们的金字塔越靠上时这种模式就越继续。

向下采样方法：1.对图像进行高斯内核卷积；2.将所有偶数行和列去除

图像的较低级别（高分辨率）是通过较高级别（低分辨率）在每个维度上扩大为原来的两倍，新增的行和列（偶数行和列）以0填充，然后使用指定的滤波器进行卷积去估计丢失像素的近似值。

向上采样方法：1.将图像在每个维度扩大到原来的两倍，以新增的行和列以0填充；2.使用原先同样的内核（x4）与方法后的图像卷积，获得新增像素的近似值在缩放过程中已经丢失了一些信息，如果想在缩放过程中减少信息的丢失，就需要用到拉普拉斯金字塔

cv.pyrUp(src)函数：其中只需要传入一个参数，代表图像资源，用于对图像做向上采样

cv.pyrDown()函数：参数传递与cv.pyrUp()一致，用于对图像做向下采样，通常也可以做图像模糊化处理

3.1.2 拉普拉斯金字塔

拉普拉斯金字塔由高斯金字塔形成，没有专用的功能，拉普拉斯金字塔图像仅表示边缘图像，它的大多数元素为0，它们通常用于图像压缩

拉普拉斯金字塔的层由高斯金字塔的层与高斯金字塔的高层的扩展版本之间的差形成

我们通过一个例子来展示拉普拉斯金字塔

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img = cv.imread(r'E:image	est06.png', )
loser_reso = cv.pyrDown(img)
higher_reso = cv.pyrUp(loser_reso)
lapPyr = img - higher_reso
test = higher_reso
loser_reso2 = cv.pyrDown(test)
higher_reso2 = cv.pyrUp(loser_reso2)
lapPyr2 = test - higher_reso2
cv.imshow('lapPyr', lapPyr)
cv.imshow('lapPyr2', lapPyr2)
cv.waitKey(0)
cv.destroyAllWindows()

 

 

3.2 使用图像金字塔进制图像融合

图像金字塔的一个应用是图像融合，如果进行简单的图像拼接，我们将两个图片堆叠在一起，会因为图像之间的不连续性看起来效果不好，在这种情况下金字塔混合图像可以无缝混合，而不会在图像中保留大量数据

想要达到图像混合的效果，需要完成以下步骤：

加载两个需要进行混合的图像

查找两张图像的高斯金字塔，然后在其高斯金字塔中找到其拉普拉斯金字塔

在每个拉普拉斯金字塔级别中加入两张图片的各一半

最后从此联合图像金字塔中重建原始图像

import cv2 as cv
import numpy as np, sys

A = cv.imread('E:/image/horse.png')
B = cv.imread('E:/image/cow.png')
# 生成A的高斯金字塔
G = A.copy()
gpA = [G]
for i in range(6):
    G = cv.pyrDown(G)
    gpA.append(G)
# 生成B的高斯金字塔
G = B.copy()
gpB = [G]
for i in range(6):
    G = cv.pyrDown(G)
    gpB.append(G)
# 生成A的拉普拉斯金字塔
lpA = [gpA[5]]
for i in range(5, 0, -1):
    GE = cv.pyrUp(gpA[i])
    L = cv.subtract(gpA[i - 1], GE)
    lpA.append(L)
# 生成B的拉普拉斯金字塔
lpB = [gpB[5]]
for i in range(5, 0, -1):
    GE = cv.pyrUp(gpB[i])
    L = cv.subtract(gpB[i - 1], GE)
    lpB.append(L)
# 现在在每个级别中添加左右两半图像
LS = []
for la, lb in zip(lpA, lpB):
    rows, cols, dpt = la.shape
    ls = np.hstack((la[:, 0:cols / 2], lb[:, cols / 2:]))
    LS.append(ls)
# 现在重建
ls_ = LS[0]
for i in range(1, 6):
    ls_ = cv.pyrUp(ls_)
    ls_ = cv.add(ls_, LS[i])
# 图像与直接连接的每一半
real = np.hstack((A[:, :cols / 2], B[:, cols / 2:]))
cv.imwrite('Pyramid_blending2.jpg', ls_)
cv.imwrite('Direct_blending.jpg', real)

编辑：黄飞