自旋涨落增强的声子磁矩

原文作者：武芳亮等

磁有序体系中声子磁矩的探索取得了进展，研究人员在反铁磁体中观测到巨大的声子磁矩及其临界涨落增强效应。该研究揭示了多体关联和自旋涨落对声子在磁有序系统获得大的磁矩及其临界现象中所扮演的关键角色。  

声子是晶格振动的集体激发，是固体中最常见也最重要的准粒子之一。对声子基本性质的理解是凝聚态物理和材料科学众多研究的基础。声子具有能量和准动量，在时间或空间反演对称性破缺的体系中，声子也可携带角动量，并具有手性[1，2]。但长久以来，人们认为声子的磁矩可以忽略不计[3]。这是因为离子的质量远大于电子，由离子绕转产生的声子轨道磁矩极其微弱，通常小于10-4玻尔磁子(μB)，比电子磁矩小4个量级，因此几乎没有可观测效应。

20世纪70年代，研究者发现稀土顺磁体CeCl3中位于109 cm-1和197 cm-1的光学声子在磁场下发生塞曼劈裂。在该体系中，声子通过与Ce离子4f 轨道晶体场激发的耦合，获得了巨大的磁矩，达到μB量级[4]。图1展示了通过塞曼效应测量声子磁矩的示意图。近期，研究者通过太赫兹光谱在拓扑非磁材料Cd3As2和PbTe中，分别观测到μB和0.01μB量级的巨大声子磁矩[5，6]。随后的理论研究发现，在“波恩—奥本海默近似”下，离子的绕转伴随着电子波包的运动，后者的轨道磁矩可以被能带的贝里曲率放大，进而贡献可观的声子磁矩[7]。上述基于顺磁或非磁体系的研究，证明了声子可以通过晶格—电荷两个自由度间的耦合获得磁矩。然而对于磁有序体系，尚未有声子磁矩的观测证据。声子磁矩在磁性体系中有着广阔的研究和应用前景。

一方面磁矩可以使声子的能量被磁场、磁序和磁畴有效调控；另一方面，声子作为磁矩的载体可以直接参与众多磁学过程。这将为基础磁学研究和自旋器件设计提供全新的可能。在磁性体系中，自旋—晶格相互作用是否能赋予声子磁矩？长程自旋关联和临界自旋涨落如何影响声子的磁性质？这些基础物理问题都亟待阐明。近期，磁有序体系中声子磁矩的探索取得了进展，研究人员在反铁磁体中观测到巨大的声子磁矩及其临界涨落增强效应[8]。

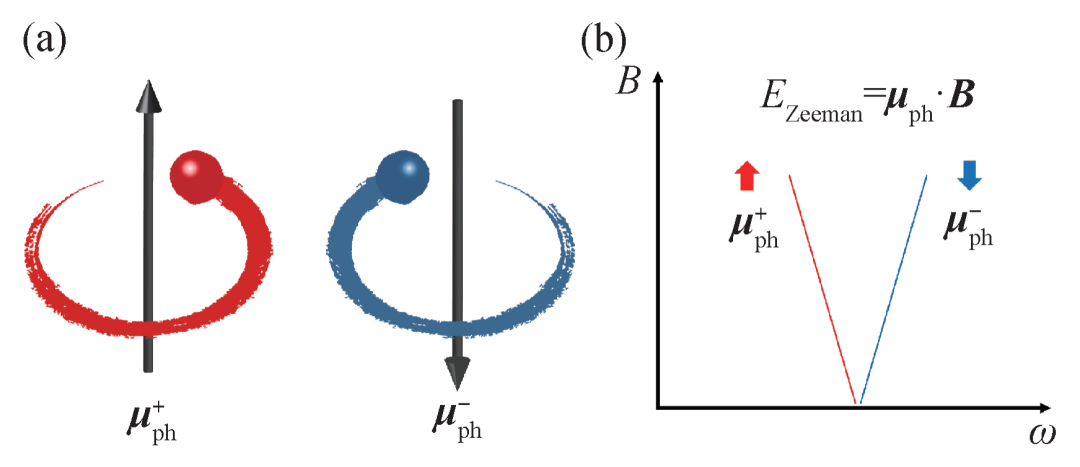
图1 (a)携带相反磁矩的一对简并声子在外磁场下发生塞曼劈裂；(b)声子磁矩(μph)可由塞曼劈裂的斜率得到

此项研究聚焦于极化反铁磁材料Fe2Mo3O8，它是绝缘体中热霍尔系数最大的材料之一[9]。该体系的热输运由声学声子主导，巨大的热霍尔效应说明自旋—晶格相互作用在该体系中非常显著。当温度低于60 K时，Fe2Mo3O8具有反铁磁序，外磁场可以驱动体系进入亚铁磁相，这为磁有序体系声子磁矩的研究提供了理想平台。

通过低波数拉曼光谱，研究人员观测到Fe2Mo3O8中位于1.3 THz(42 cm-1)的激发模式(P1)。该光谱信号在室温下仍清晰可见，这排除了其为磁激发的可能。非弹性中子散射测量进一步确认了该模式的声子属性。通过光谱分析和第一性原理计算，研究者发现P1模式由一对携带相反角动量的手征声子构成。该模式中磁性原子的位移主要来自四面体Fe的面内绕转，如图2(a)所示。通过交叉圆偏振磁光拉曼光谱，研究人员发现这对简并的手征声子在磁场下发生了显著的塞曼劈裂(图2(b))。携带相反角动量的手征声子其频率随磁场发生线性偏移。由塞曼劈裂的斜率可得P1声子的磁矩为0.11μB，较一般固体高出3个量级以上。该实验给出了磁有序系统中声子磁矩的确凿证据。进一步研究发现，P1声子的磁矩来源于晶格与自旋自由度的耦合。在Fe2Mo3O8中，两支反铁磁自旋波分别位于2.6 THz和3.4 THz。P1声子正是通过与它们的非共振耦合获得磁矩，这也解释了P1在相变温度以上，随温度升高而发生的频率蓝移。因为随着与磁振子耦合的消失，P1在相变温度以上逐渐回归其未耦合的本征频率。

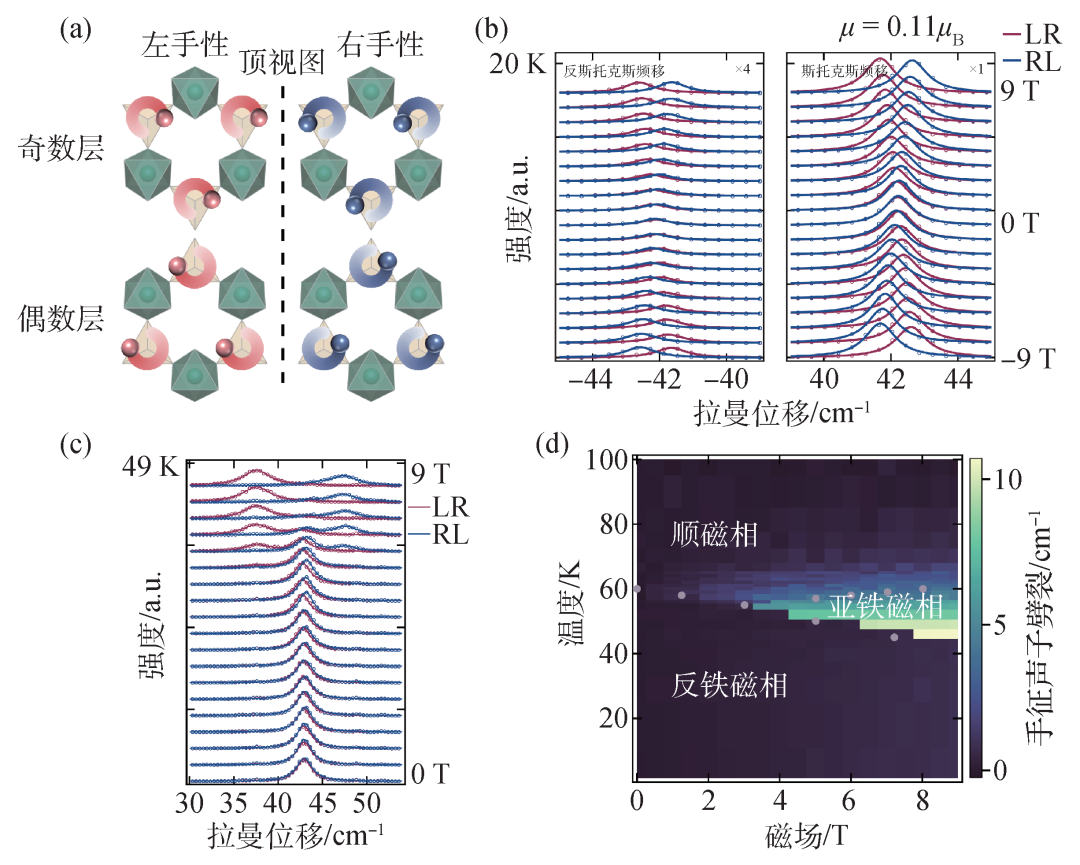
图2 (a)P1声子中Fe离子位移示意图。其中磁性原子的运动主要由处于铁氧四面体位置的Fe离子在ab面内的圆偏振运动构成，相邻层之间绕转相位相反，是一支光学声子；(b)圆偏振磁光拉曼光谱测量P1的塞曼劈裂。20 K时，P1声子的塞曼劈裂对应于0.11μB声子磁矩。LR表示左圆偏振光激发右圆偏振光探测，而RL则表示右圆偏振光激发左圆偏振光探测；(c)P1手征声子的劈裂在亚铁磁相显著增大；(d)手征声子劈裂对磁场和温度的依赖关系，其中体现巨大声子劈裂的区域与亚铁磁相区域重合

为了探究磁相变对声子磁矩的影响，研究人员继续通过圆偏振分辨的拉曼光谱追踪P1声子随外磁场和温度的变化。磁场可以驱动Fe2Mo3O8由反铁磁相进入亚铁磁相。如图2(c)所示，当进入亚铁磁相时(6.5 T)，手征声子劈裂陡然变大，达到10 cm-1，高达声子共振频率的24%，该比例是目前报道的手征声子劈裂的最大值。图2(d)展示了不同温度和磁场下手征声子的劈裂大小。其中代表巨大声子劈裂的黄色区域与由磁化测量标定的亚铁磁相吻合。

最有趣的现象发生在反铁磁相到顺磁相的转变区域。通过提取不同温度下P1声子的磁矩，研究人员发现了在相变温度(60 K)附近，P1声子的磁矩展现出高达600%的增强。在58 K时，P1声子的磁矩从低温时的0.11μB迅速增大到0.68μB，如图3(a)所示。虽然声子和磁振子的非共振耦合可以给出该体系低温反铁磁相下的声子磁矩，但不足以解释其在相变点附近的6倍增强。通过深入研究，人们发现该体系的准二维亚铁磁涨落是导致P1声子磁矩增强的主要原因。Fe2Mo3O8的反铁磁序可以看作是准二维的亚铁磁序，经层间耦合后形成的三维结构。Fe2Mo3O8在相变温度附近有着强烈的亚铁磁自旋涨落，这一点被磁化率测量所验证。相变温度附近，外磁场及其诱导出的分子场作为总的等效磁场作用于P1声子，其中分子场被亚铁磁自旋涨落所放大，导致了声子磁矩的增强。P1声子磁矩在60 K以上并没有马上消失，这是因为声子和顺磁磁振子(paramagnon)发生耦合。在更高温度下，顺磁磁振子进一步失去相干性，而声子磁矩最终消失。研究人员采用蒙特卡罗模拟成功复现了声子磁矩的临界涨落增强现象，验证了该理论解释的可靠性，如图3(b)所示。这一简单的平均场图像也解释了亚铁磁相中P1手征声子的巨大劈裂来源于亚铁磁相的分子场。

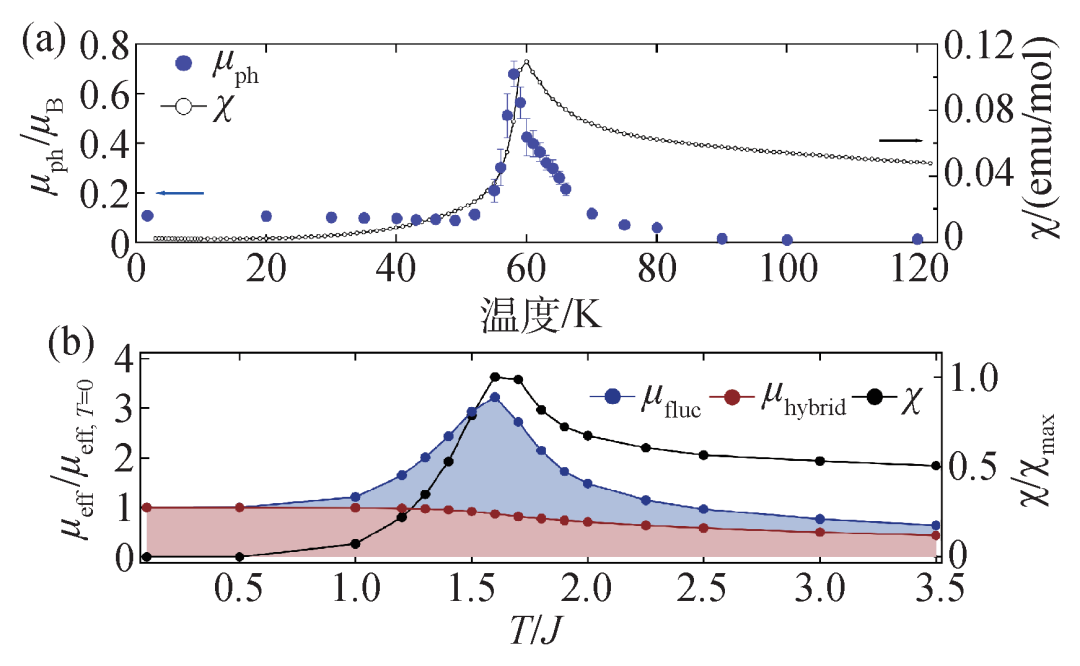
图3 声子磁矩随温度的变化   (a)实验数据显示，在相变温度60 K附近，声子磁矩展现出高达600%的增强，黑色空心圆为磁化率曲线；(b)蒙特卡罗模拟成功复现实验结果。其中蓝色部分代表自旋涨落贡献的声子磁矩，红色部分代表与磁振子杂化获得的声子磁矩，黑色实心圆代表磁化率曲线

综上所述，此项研究发现了反铁磁体系Fe2Mo3O8中巨大的声子磁矩，并且首次观测到自旋涨落对声子磁矩的增强，高达600%，声子磁矩达到0.68μB，接近电子磁矩量级。理论研究揭示了多体关联和自旋涨落对声子在磁有序系统获得大的磁矩及其临界现象中所扮演的关键角色。在基础磁学方面，该发现更新了对声子磁矩的认知；在应用方面，使得以声子磁矩为信息载体的新型自旋器件成为可能。最后，在先前研究中，Fe2Mo3O8中的P1声子被误认为是具有电偶极活性的磁激发[10]，即电磁振子(electromagnon)，而此项研究不仅阐明了P1的声子属性，也揭示了电磁振子的一种可能的声子起源。类似的机制也可能存在于其他I-型多铁体系。这为理解和调控多铁体系中的低能元激发提供了新的视角。

参考文献

[1] Zhang L，Niu Q. Phys. Rev. Lett.，2014，112：085503

[2] Zhang L，Niu Q. Phys. Rev. Lett.，2015，115：115502

[3] Juraschek D M，Spaldin N A. Phys. Rev. Mater.，2019，3：064405

[4] Thalmeier P，Fulde P. Z. Phys. B，1977，26：323

[5] Baydin A et al. Phys. Rev. Lett.，2022，128：075901

[6] Cheng B et al. Nano Lett.，2020，20：5991

[7] Ren Y，Xiao C，Saparov D et al. Phys. Rev. Lett.，2021，127：186403

[8] Wu F et al. Nat. Phys.，2023，https://doi.org/10.1038/s41567-023-02210-4

[9] Ideue T，Kurumaji T，Ishiwata S et al. Nat. Mater.，2017，16：797

[10] Kurumaji T et al. Phys. Rev. B，2017，95：020405

编辑：‘黄飞’