

3.GraphSAGE[9]:generalized aggregation方法
描述
1.graph embedding(GE)
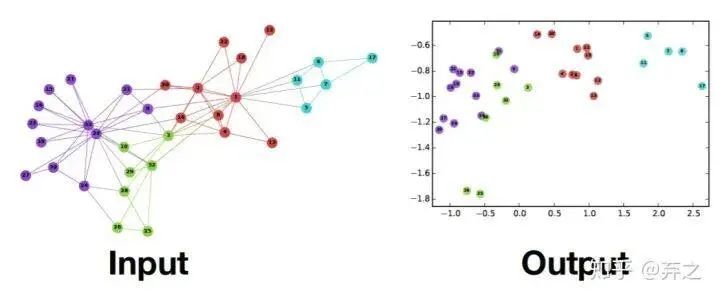
GE做的事情是将图表示成为低维向量,类似与nlp将词、句子等embedding。distributed representation的一体化过程,万物皆可embedding。
- 将图中的节点表示成低维、实值、稠密的向量形式,使得得到的向量形式可以在向量空间中具有表示以及推理的能力,这样的向量可以用于下游的具体任务中。例如用户社交网络得到节点表示就是每个用户的表示向量,再用于节点分类等;
- 将整个图表示成低维、实值、稠密的向量形式,用来对整个图结构进行分类;
在图中最重要的两个部分就是
- encoder:map到低维向量
- similarity function:如何度量相似度(什么样的node的embedding应该相似?)
www-18有个很好的tutorial:Representation Learning on Networks[1],可以参考
1.1.图中学习的分类
- 归纳学习(Inductive Learning):先从训练样本中学习到一定的模式,然后利用其对测试样本进行预测(即首先从特殊到一般,然后再从一般到特殊),这类模型如常见的贝叶斯模型。在GAT中
- 转导学习(Transductive Learning):先观察特定的训练样本,然后对特定的测试样本做出预测(从特殊到特殊),这类模型如k近邻、SVM等。在GAT中采用的是在Cora 数据集上优化网络结构的超参数,应用到Citeseer 数据集
1.2.相似度度量方法
度量方式可以进行如下分类
- Adjacency-based Similarity:相邻节点相似,能表征这两个是否有连接
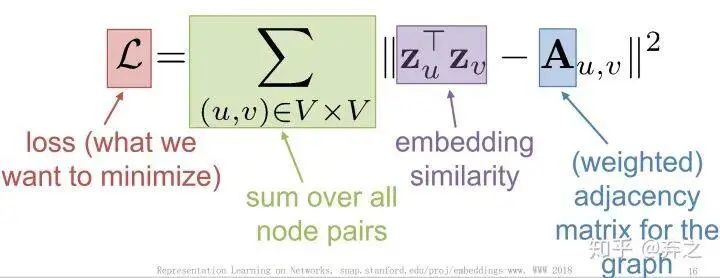
- Multi-hop Similarity:考虑k跳的neighbor
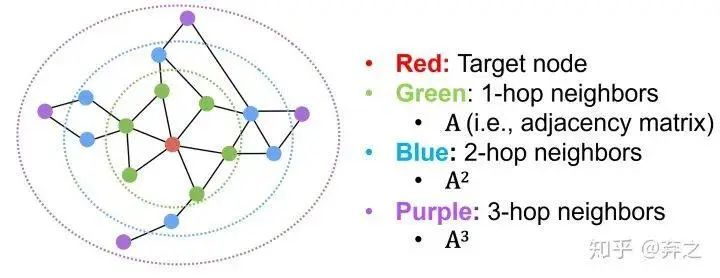
典型代表就是GraRep(Cao et al, 2015)和HOPE (Yan et al., 2016)了,一个考虑不同跳数分别训练然后concatenate,一个考虑neighbor的重复程度。
- Random Walk Approaches:典型代表是deepwalk和node2vec,采用和nlp的相似方法,共现频率来度量。
- GNN阶段:neighborhood aggregation
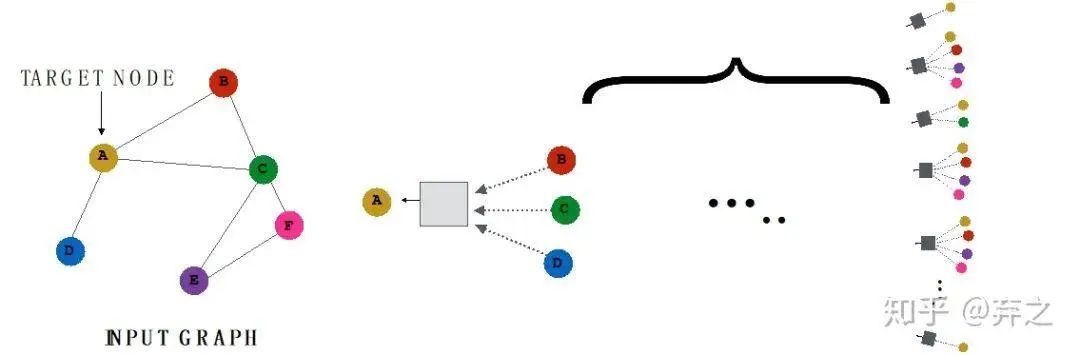
neighborhood aggregate的方法可以对每个target node来刻画以它为中心的计算图,如
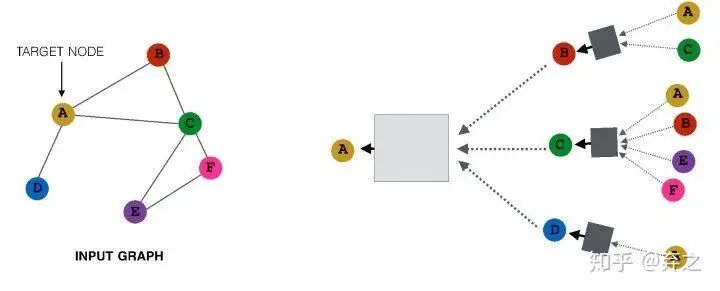
对于每一个node,都构成了一个计算图,而且每个node的计算图都有差别
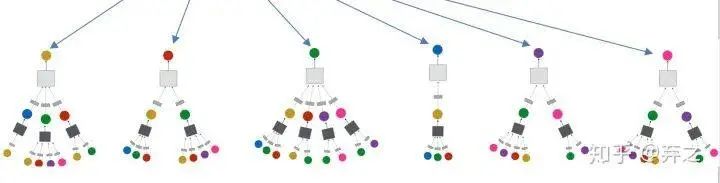
我们可以看到GNN逐渐成形了,考虑简单的aggregate方式可以表示成这个样子
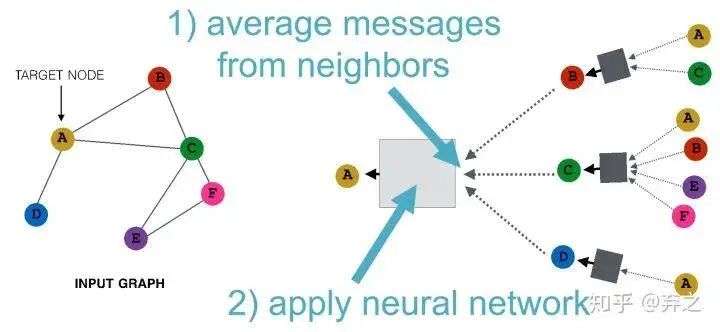
数学表示也十分清晰了,如下图, 就是节点 的第 个时间步(或第 layer)的embedding
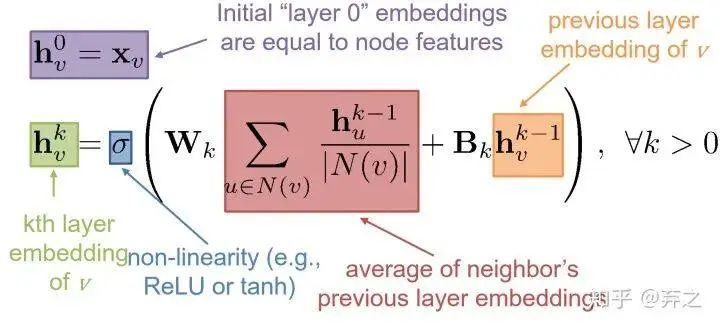
这就好家伙了,上图中一些参数就可以generalize到一些unseen的点了,如下图
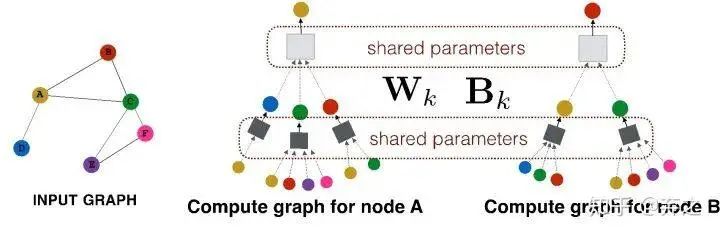
这种能力称之为inductive capability
早期迈向neural的过程借鉴了nlp的方法,如deepwalk[2]利用word2vec的方法,因为语料中词语出现的次数与在图上随机游走节点被访问到底的次数都服从幂律分布,采用随机游走进行采样出序列,然后按照word2vec的方法进行训练。
word2vec出现在2013年,deepwalk 14年就出现了,紧随其后。
后来来也出现了很多,如Line,node2vec,struc2vec,听名字就知道,Line和node2vec是在描述图像时刻画节点的embedding,不过在游走的方式上进行探索,是DFS还是BFS还是both呢?到了struc2vec开始走节点空间结构的相似性这条路了。
其实这些已经跨入到neural的阶段了,但是还用的比较初级,没有专门为graph设计的neural的模型,探索阶段。
2.Graph neural network
2.1.Graph convolutional network(GCN)[3][4]
2.1.1.引子:热传播模型
图卷积是基于热传播模型,即两个点之间热传播的速度和两点之间温度差值成正比,把这个热传播模型推广到图上就是信息传播的速度关系[5]。
假设它当前的温度为,在一个链条上的热量传播那么就有:
和单元的比热容、质量有关是个常数。右边第一项是下一个单元向本单元的热量流入导致温度升高,第二项是本单元向上一个单元的热量流出导致温度降低。这是一个二阶差分,即二阶导数。
而且是相同算子的二阶导,在高纬空间中是所有非混合二阶偏导数之和,称为拉普拉斯算子。
其中 这个符号代表的是对各个坐标二阶导数的加和,现在的主流写法也可以写作 。
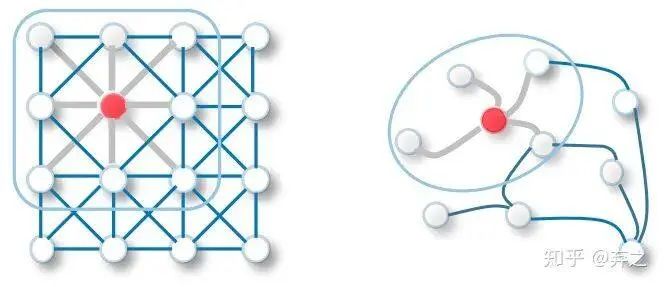
在离散图模型中是相似的,和链条热传播不同的是没有了上一个和下一个单元,有的是该节点所有的邻接节点(邻接矩阵刻画),所以同样的方式刻画为
其中 是这个图的邻接矩阵,即所有相邻节点的流入流出关系加和构成了 这个节点温度总的变化。
我们不妨用乘法分配律稍微对上式做一个推导:
即可以写成这样:
然后我们定义向量 ,那么就有:
其中 被称为度矩阵,只有对角线上有值,且这个值表示对应的顶点度的大小。整理整理,我们得到:
回顾刚才在连续欧氏空间的那个微分方程:
二者具有一样的形式。这实际上是同一种变换在不同空间上的体现。 就是其中最简单常用的图上的拉普拉斯算子矩阵。
GCN的neighborhood aggregation
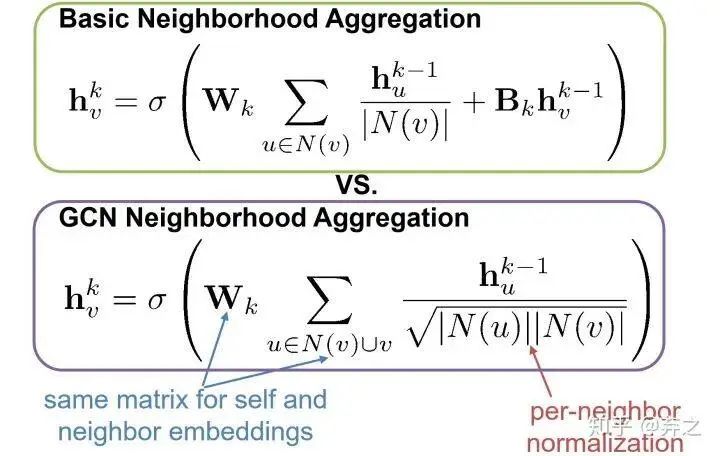
因为是热传播模型,流动的feature要流入每一个邻接节点,所以加入了一个normalization,即节点的feature需要对所有neighbor取均值之后再进行流动。
2.1.2.热传播在graph上的求解:傅里叶变换
假设在图中各个结点流动的东西不是热量,而是特征(Feature),而是消息(Message),那么问题自然而然就被推广到了GCN。所以GCN的实质是什么,是在一张Graph Network中特征(Feature)和消息(Message)中的流动和传播。
由于很多东西在频域上会更好解决,而且拉普拉斯矩阵与傅里叶不谋而合,所以频域上解决的方案来做。先来推导下傅里叶变换和拉普拉斯算子的关系

关于傅里叶变换的理解,可参照我之前的博客[6]。所以,傅里叶变换就被推广为时域信号与特定空间上拉普拉斯算子特征函数的积分。
理解下这个公式,实对称矩阵的特征空间的所有基能够张出整个线性空间且它们两两正交,所以无论是拉普拉斯算子 还是拉普拉斯矩阵 ,它们的特征空间是一个满秩且基两两正交的空间,所以把欧氏空间的 推广到图空间的 的这一组特征向量。正是同一个关系(Message Passing),同一种变换,在不同空间下的体现。
现在我们已经得到了graph空间上的拉普拉斯算子 ,只需要对 求出其特征向量貌似就可以傅里叶变换了。等等,我们到底需要傅里叶变换干嘛?经过前面的铺垫,傅里叶变换做了一个空间的变换,而这个空间里的卷积就非常绝-卷积定理卷积和乘积的变换。
在传统的谱图卷积下,由卷积定理:
函数卷积的傅里叶变换是函数傅里叶变换的乘积。具体分为时域卷积定理和频域卷积定理,时域卷积定理即时域内的卷积对应频域内的乘积;频域卷积定理即频域内的卷积对应时域内的乘积,两者具有对偶关系。
时域卷积(时域内的卷积对应频域内的乘积)如下:
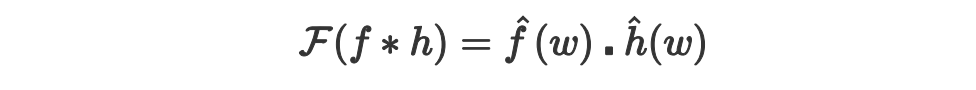
为了更好理解,证明方法如下:
因此,卷积的傅里叶等于傅里叶的积。
做逆变换
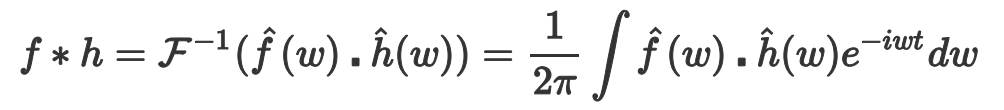
所以现在傅里叶域做乘积,然后做傅里叶逆变换,等价于在原空间直接做卷积。
2.2.分析下graph neural中哪些东西可以做?
如以上分析,本质是图上特征流动进行建模,然后利用傅里叶变换作为解决方案。
建模的方法还可以更加丰富,不一定流动速度非要和温度查成正比,可以用更加复杂的模型,如神经网络等来进行更加复杂的建模。
建模时也可以不是单纯对相邻节点的影响进行简单的加和,在实际建模中,我们的Aggregate不一定是加和,可以把Aggregate推广成各种操作例如Sum Pooling,例如LSTM,例如Attention
解决方案也是如此,不一定非要在傅里叶域做,傅里叶做的谱图卷积,现在也可以直接在原空间域做卷积-Spatial Convolution,如DCNN[7],GAT[8]等
2.3.损失函数
对于无监督的训练,其实就和nlp的预训练类似,训练出embedding,训练好之后再接下游任务。
对于有监督的训练来说,如节点分类,一个比较简单的方案就是对每个node的embedding接一个全连接层,就得到了一个损失函数
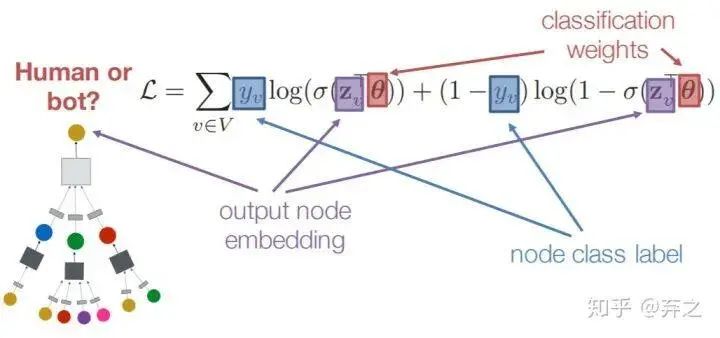
就是全连接层的权重。
3.GraphSAGE[9]:generalized aggregation方法
GCN是谱图方法的代表,那么GraphSAGE就是非谱图方法的代表。
如何进行更好的aggregate呢?
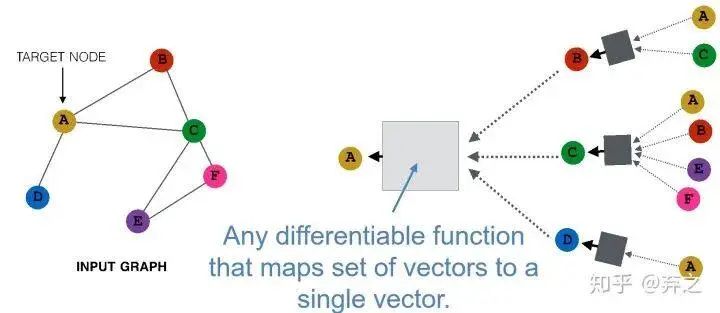
最后的这个黑盒里面可以装的东西就多了,只要能把多个vector最后map到一个最终的vector就行
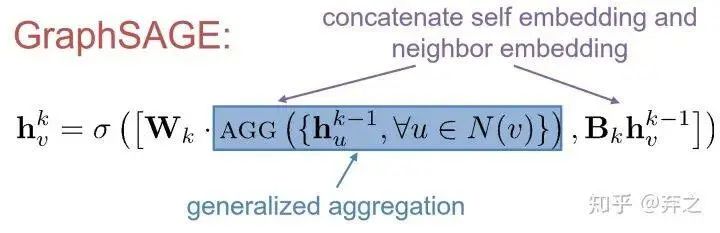
GraphSAGE则是将aggregate后的neighbor和本身的self-embedding这两个concatenate到一起作为新的embedding,而不是传统的把所有的embedding 加权求和,在原始论文中,作者提出这是一种很好的'skip connection'的方法。当然AGG也可以有很多变体,不一定非要是aggregate,也可以是pool,lstm等等。
4.Gated Graph Neural Networks[10]:go deeper with RNN
GCNs and GraphSAGE generally only 2-3 layers deep,因此对于每个node所构成的aggregate图比较浅,如何走得更深呢?
可能会存在overfit或者梯度消失/爆炸,所以我们希望一个简化可重用的模型,RNN!
每一层都使用相同的RNN单元,因为每个node 的neighbor的数量不同,所以先对所有neighbor做aggregate,我们称之为“message”

就是节点v在step k的message
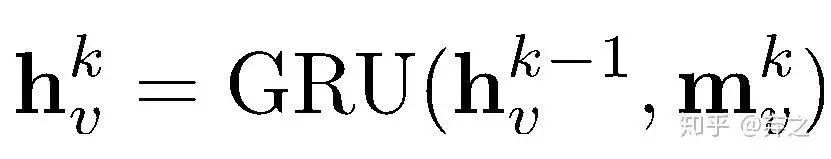
然后利用GRU对message和上一步状态做处理得到新的状态。
5.Graph level的embedding
直接把图中所有node的embedding相加[11]
引入一个virtual node来代表graph,并用神经网络进行训练[12]
6.Graph attention network
利用attention在graph中动态确定和neighbor的权重,并利用mask只考虑邻近的neighbor。
这篇文章用的attention与transfomer并不相同,只有一个突然formation matrix,而不是像attention中有q,k,v三个transformation
利用一个单层的全连接网络来确定系数,将这两个vector contatenate在一起输入。然后进行softmax归一化
即
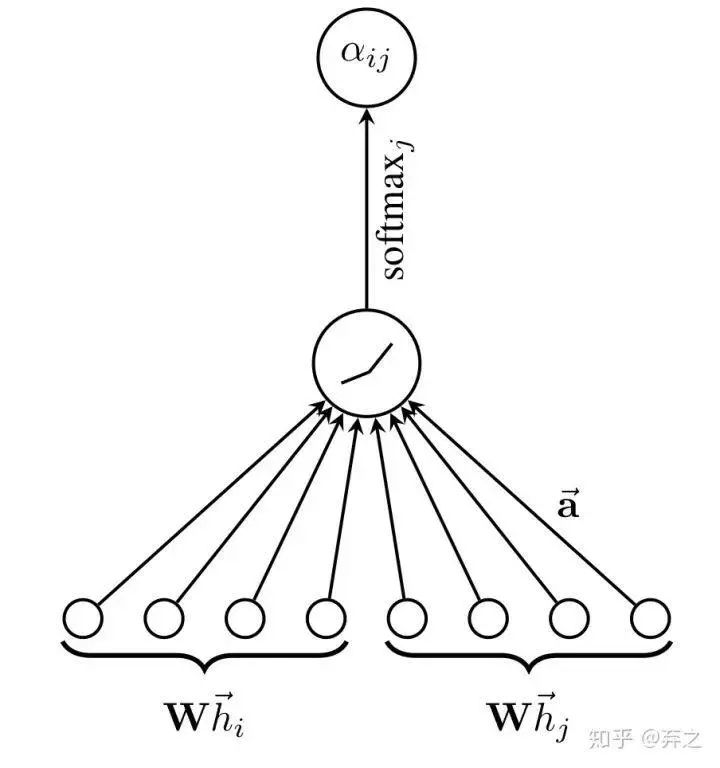
同时还采用了multi-head attention的机制
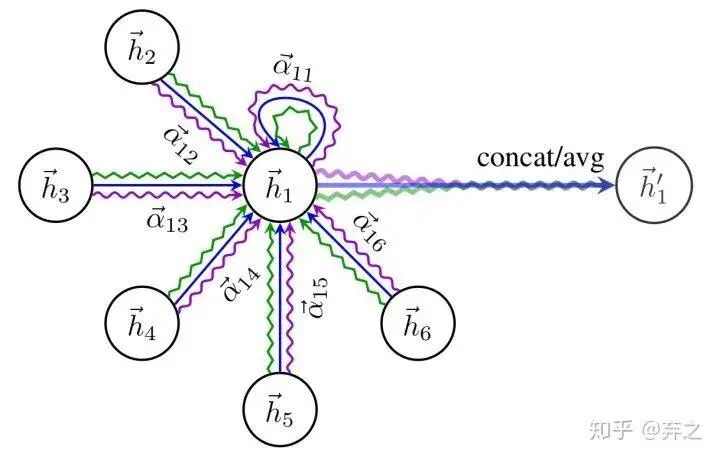
得到归一化的注意力系数后,使用归一化的值计算对应特征的线性组合,作为每个顶点最后的输出特征(最后可以加一个非线性层,σ):
就是GAT输出的节点i融合了邻域信息的新特征
优点(摘自原文)
- 计算高效:self-attention层的操作可以在所有的边上并行(所有边上算出的注意力系数可以共享),输出特征的计算可以在所有顶点上并行。没有耗时的特征值分解。单个的GAT计算F ′个特征的时间复杂度可以压缩至 (前面是算所有node的 的复杂度,后面是算所有边注意力系数的),F是输入的特征数,|V|和|E|是图中顶点数和边数。复杂度与Kipf & Welling, 2017的GCN差不多。multi-head 中单个head的计算完全独立且可以并行化。
- 鲁棒性更强:和GCN不同,本文的模型可以对同一个 neighborhood的node分配不同的重要性,使得模型的capacity大增。
- 注意力机制以一种共享的策略应用在图的所有的边上, 也是一种局部模型。在使用 GAT 时,无需访问整个图,而只需要访问所关注节点的邻节点即可,解决了之前提出的基于谱的方法的问题。因此这个方法有几个影响:
- 图不需要是无向的,可以处理有向图(若 不存在,仅需忽略 即可)
- 可以直接应用到 inductive learning:包括在训练过程中在完全未见过的图上评估模型的任务上。
- GraphSAGE为每一个node都抽取一个固定尺寸的neighborhood,在计算的时候就不是所有的neighbor都能参与其中(不是所有都直接相连的neighbor都参与了aggregate吗?)。此外,Hamilton的这个模型在使用基于LSTM的方法的时候假设了每个node的neighborhood的node一直存在着一个顺序(RNN有输入顺序)。但是本文提出的方法就没有这个问题,每次都可以将neighborhood所有的node都考虑进来,而且不需要事先假定一neighborhood的顺序。
7.application example
如node classification和link prediction
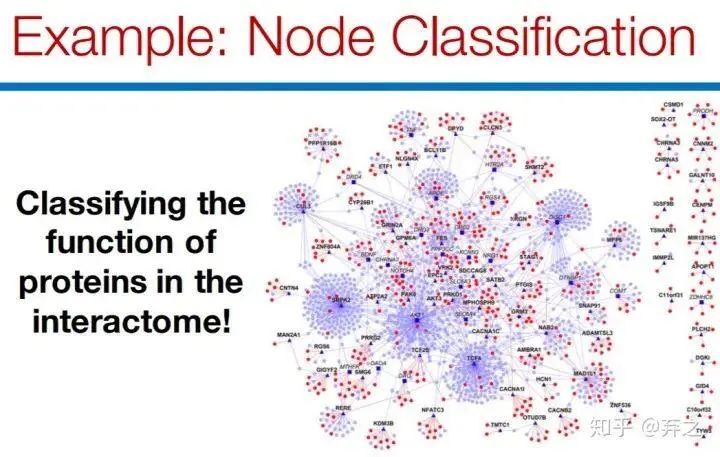

在实际的运用中,可以运用在
- recommendation
- Computational biology
- Practical insights
8.彩蛋:卷积的含义
卷积又称褶积,来源于数字信号的处理
卷积的形式可以分两类:
连续形式:
离散形式:
先对g函数进行翻转,然后再把g函数平移到n,然后滑动叠加,这就是卷积的过程。
我们可以考虑在原始的数字信号处理中,对于一个输入信号 ,我们想要得到一个在特定时间下的输出信号, 可以看成信号的衰减过程(单位冲击响应函数), 可以看成是想要得到输出信号的时间。
比如以一天24h为例,我们希望得到一天结束时总的信号。在0时产生的信号 ,那么在24小时后衰减 ,在1时产生的信号为 ,那么这一天结束时衰减 ,以此类推,把每个时刻产生的信号以及到一天结尾时衰减程度相乘相加,就是所谓的卷积了,得到这一天结束时总的信号了。
那么对于图片呢?
其实仍然是矩阵对应元素的相乘相加,只是矩阵 可以看成filter是翻转了。

但是其实CNN中用的更确切应该称为互关(co-relation),因为filter是没有进行翻转的,可以对比一下这两者表达式的区别
co-relation:
convlution:
但是其实在CNN中不必那么严格的进行区分,学习一个翻转前和翻转后的filter并无不同,但是在数字信号处理中是不同的。
卷积拥有更多美好的性质,如交换律结合律等,在CNN中互关基本也都被称为卷积了。而且当核对称的时候,其实就完全一样了。
-
9DBL02x3-04x3-06x3-08x3 系列数据表2023-06-30 408
-
3A9T3A9Y3A9U锂电池保护芯片规格书2021-09-16 1666
-
3-1879665-9 H830K9BYA 通孔式电阻器2021-07-25 179
-
3-2176403-9 3550 39R 1%2021-07-01 107
-
9-328666-3 FERRULE, STEP DOWN, PLTD2020-12-08 292
-
一种新的数值电磁分析广义反嵌方法2019-03-01 1155
-
Carrier Aggregation Fundamentals2017-01-13 674
-
Altium Designer 9使用方法2016-12-20 1298
-
Altium_Designer9使用方法2012-08-05 3142
-
d3dx9_32.dll下载2009-11-28 812
全部0条评论

快来发表一下你的评论吧 !

