

四足机器人接触检测和模型
描述
接触检测
步态规划器给出的接触序列是严格按照时间进行周期性计算的。而在实际运行当中,由于地形的不平整,又或者存在坡度等情况,腿部会发生提前或者延迟接触等情况,因此只靠步态规划器给出的接触序列来控制机器人往往是不可靠的。
因此这里提出一个基于卡尔曼滤波的概率接触检测。其综合考虑了步态规划其给出的恒定接触序列,足端高度,地形的不平整性,以及通过关节编码器数据所计算出来的关节力矩,来提高接触检测的精度,同时减少了腿部由于电机力矩控制所引起的关节回弹现象
预测模型
卡尔曼滤波器的标准预测方程如下:

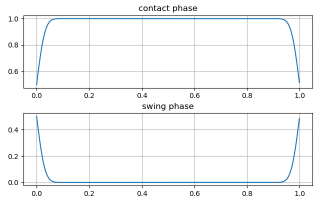
该模型有以下函数曲线:
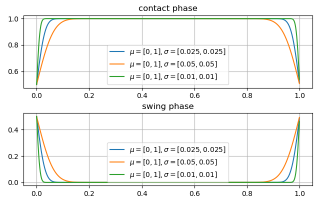
当参数(μ,σ)取不同值时,图像如下所示,可以看出,σ取不同值时,曲线的曲率会有所变化,当曲率比较大时,其预测结果更精确,但是许用误差范围较小,容易造成系统的不稳定;
而当曲率变小时,预测模型的稳定性更强,其许用误差范围较大,但预测结果相对来说没那么精确,实际参数的选取可根据实机结果进行调整:
测试代码如下:
def prediction_model(phi, state, params):
"""
Given the gait schedule and the current phase of a leg,
the gait scheduler provides an expected contact state of
each leg
:param phi: phase
:param state: contact state
:param params: [mu, mu_bar, sigma, sigma_bar]
mu = [mu1, mu2] and so on
:return: the probability of contact
"""
mu0, mu1 = params[0]
mu0_bar, mu1_bar = params[1]
sigma0, sigma1 = params[2]
sigma0_bar, sigma1_bar = params[3]
a = math.erf((phi-mu0)/(sigma0*np.sqrt(2)))
+ math.erf((mu1-phi)/(sigma1*np.sqrt(2)))
b = 2+math.erf((mu0_bar-phi)/(sigma0_bar*np.sqrt(2)))
+ math.erf((phi-mu1_bar)/(sigma1_bar*np.sqrt(2)))
if state == 1:
prob = 0.5 * (state * a)
else:
prob = 0.5 * (state * b)
return prob
因此,对于k个接触点,该预测模型可以作为系统的瞬时输入为:
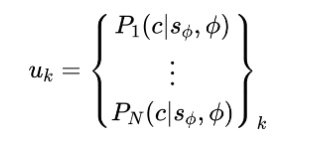
协方差矩阵如下,该矩阵表示我们对预测精度的信赖程度

由于我们只关注瞬时接触检测(通过融合当前可用的测量),所以状态矩阵和输入矩阵被定义为如下:
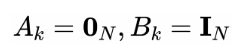
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
四足机器人步态规划与接触状态2023-11-16 1583
-
四足机器人遍地开花,四足机器人的市场有多大2022-04-06 2564
-
ANYmal四足机器人的相关资料推荐2021-12-31 1771
-
如何完整的组装四足机器人?2021-09-24 3090
-
四足机器人的机构设计2021-09-15 1892
-
求六足机器人的图纸2019-03-26 3910
-
四足机器人2018-09-29 10503
-
四足仿生机器人2016-08-19 6267
-
什么是龙人四足机器人?2016-03-24 8802
-
【OK210申请】四足轮式机器人2015-06-25 2296
-
stm32红外六足机器人2014-03-27 10264
-
双足机器人2013-11-25 3117
-
六足机器人2013-06-06 3549
-
四足步行机器人的弯道行走2012-08-12 2903
全部0条评论

快来发表一下你的评论吧 !

