

六自由度机械臂三次多项式插值法
描述
对串联机械臂而言,轨迹规划可以分为:关节空间轨迹规划和笛卡尔空间轨迹规划。关节空间轨迹规划是把机器人的关节变量变换成跟时间的函数,然后对角速度和角加速度进行约束。
笛卡尔空间轨迹规划是把机器人末端在笛卡尔空间的位移、速度和加速度变换成跟时间的函数关系。
由于在关节空间中进行轨迹规划是直接用运动时的受控变量规划轨迹,有着计算量小,容易实时控制,而且不会发生机构奇异性等优点,所以经常被采用。
现以一维的轨迹为研究对象,利用三次多项式插值法和五次多项式插值法分别对其进行轨迹规划,通过对比两种插值法的效果,选取效果更优者对六自由度机械臂进行轨迹规划。
** 三次多项式插值法**
三次多项式有4个待定系数,可同时对起始点和目标点的角度和角速度给出约束条件。
数学推导


MATLAB代码
%三次多项式插值法
clear;
clc;
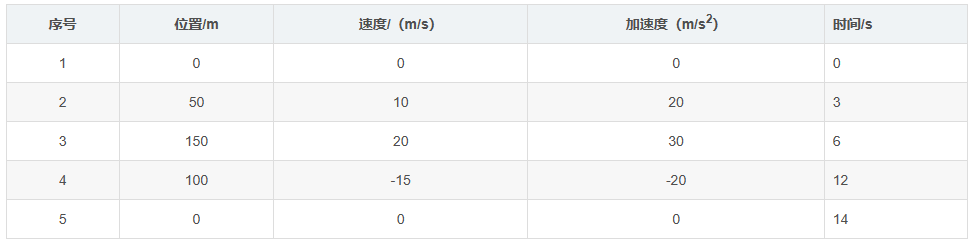
q_array=[0,50,150,100,0];%指定起止位置
t_array=[0,2,4,8,10];%指定起止时间
v_array=[0,10,20,-15,0];%指定起止速度
t=[t_array(1)];q=[q_array(1)];v=[v_array(1)];a=[0];%初始状态
for i=1:1:length(q_array)-1%每一段规划的时间
a0=q_array(i);
a1=v_array(i);
a2=(3/(t_array(i+1)-t_array(i))^2)*(q_array(i+1)-q_array(i))-(1/(t_array(i+1)-t_array(i)))*(2*v_array(i)+v_array(i+1));
a3=(2/(t_array(i+1)-t_array(i))^3)*(q_array(i)-q_array(i+1))+(1/(t_array(i+1)-t_array(i))^2)*(v_array(i)+v_array(i+1));
ti=t_array(i)+0.001:0.001:t_array(i+1);
qi=a0+a1*(ti-t_array(i))+a2*(ti-t_array(i)).^2+a3*(ti-t_array(i)).^3;
vi=a1+2*a2*(ti-t_array(i))+3*a3*(ti-t_array(i)).^2;
ai=2*a2+6*a3*(ti-t_array(i));
t=[t,ti];q=[q,qi];v=[v,vi];a=[a,ai];
end
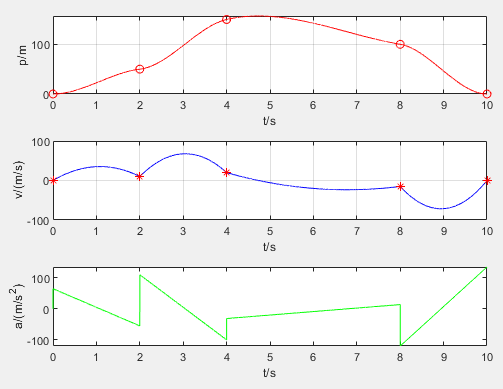
subplot(3,1,1),plot(t,q,'r'),xlabel('t/s'),ylabel('p/m');hold on; plot(t_array,q_array,'o','color','r'),grid on;
subplot(3,1,2),plot(t,v,'b'),xlabel('t/s'),ylabel('v/(m/s)');hold on;plot(t_array,v_array,'*','color','r'),grid on;
subplot(3,1,3),plot(t,a,'g'),xlabel('t/s'),ylabel('a/(m/s^2)');hold on;
% 指定文件夹保存图片
filepath=pwd; %保存当前工作目录
cd('C:UsersAdministratorDesktoppic') %把当前工作目录切换到图片存储文件夹
print(gcf,'-djpeg','C:UsersAdministratorDesktoppicsan.jpeg'); %将图片保存为jpg格式,
cd(filepath) %切回原工作目录
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
机械臂五次多项式插值法介绍2023-11-17 3514
-
计算机数值方法概念及机器人轨迹控制中点插补与三次样条函数2020-08-04 2900
-
使用SimMechanics实现六自由度的机械臂仿真研究2019-11-12 1953
-
4自由度机械臂的制作图解2019-10-09 11492
-
采用LabVIEW实现四自由度机械臂运动控制系统设计2019-05-06 4136
-
为什么最好的机械臂是7个自由度而不是6个自由度2019-03-17 27648
-
6自由度机械臂点到点5次多项式插值轨迹规划2019-03-13 5597
-
基于六维线性插值的六自由度机械臂逆运动学方程求解方法2018-03-29 1426
-
分享最好的机械臂是7个自由度的原因2018-02-07 18820
-
多项式插值算法框架2018-01-05 835
-
基于模糊PD算法的三自由度机械臂遥操作双边控制_邱恒2017-01-21 1049
-
基于多项式插值函数的翼型参数化设计方法2016-12-29 602
-
三次多项式型段内加减速控制新方法2016-05-03 663
-
六自由度机械臂的运动规划2012-02-17 2941
全部0条评论

快来发表一下你的评论吧 !

