电阻—电容(RC)低通滤波器的用途和特性

分享一篇科普文了解一下电阻—电容（RC）低通滤波器是什么，以及在何处使用它们能让你更好的掌握高端电路设计实战。本文将介绍滤波的概念，并详细说明电阻—电容（RC）低通滤波器的用途和特性。

时域和频域

当您在示波器上查看电信号时，您会看到一条线，表示电压随时间的变化。在任何特定时刻，信号只有一个电压值。您在示波器上看到的是信号的时域表示。

典型的示波器跟踪显示非常直观，但也有一定的限制性，因为它不直接显示信号的频率内容。而与时域表示相反就是频域，其中一个时刻仅对应于一个电压值，频域表示（也称为频谱）通过识别同时存在的各种频率分量来传达关于信号的信息。

什么是滤波器？

滤波器是一个电路，其去除或“过滤掉”频率分量的特定范围。换句话说，它将信号的频谱分离为将要通过的频率分量和将被阻隔的频率分量。

如果您对频域分析没有太多经验，您可能仍然不确定这些频率成分是什么，以及它们如何在不能同时具有多个电压值的信号中共存。让我们看一个有助于澄清这个概念的简短例子。

假设我们有一个由完美的5kHz正弦波组成的音频信号。我们知道时域中的正弦波是什么样的，在频域中我们只能看到5kHz的频率“尖峰”。现在让我们假设我们激活一个500kHz振荡器，将高频噪声引入音频信号。

在示波器上看到的信号仍然只是一个电压序列，每个时刻有一个值，但信号看起来会有所不同，因为它的时域变化现在必须反映5kHz正弦波和高频噪音波动。

然而，在频域中，正弦波和噪声是在一个信号中同时存在的单独的频率分量。正弦波和噪声占据了信号频域表示的不同部分（如图1所示），这意味着我们可以通过将信号引导通过低频并阻挡高频的电路来滤除噪声。

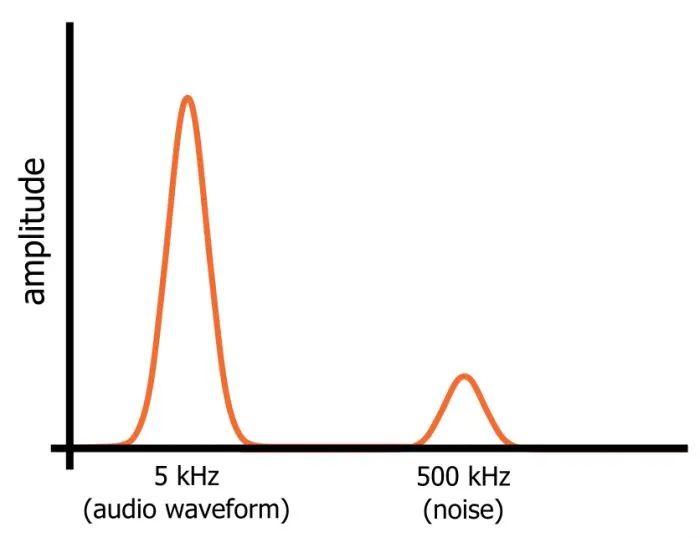
图1：正弦波和噪声信号频域的不同部分分布

滤波器的类型

滤波器可以放在与滤波器频率响应的一般特征相对应的广泛类别中。如果滤波器通过低频并阻止高频，则称为低通滤波器；如果它阻挡低频并通过高频，它就是一个高通滤波器。还有带通滤波器，其仅通过相对窄的频率范围，以及带阻滤波器，其仅阻挡相对窄的频率范围（图２）。

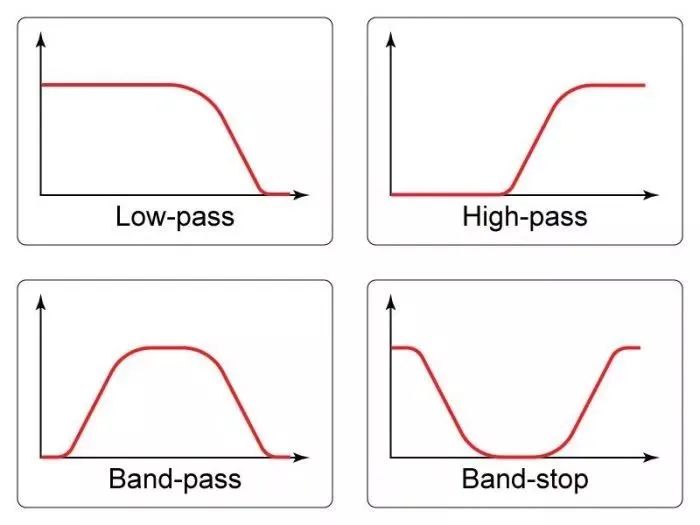
图２：各滤波器频域表示

还可以根据用于实现电路的组件类型对滤波器进行分类。无源滤波器使用电阻器，电容器和电感器，这些组件不具备提供放大的能力，因此无源滤波器只能维持或减小输入信号的幅度。另一方面，有源滤波器既可以滤波信号又可以应用增益，因为它包括有源元件，如晶体管或运算放大器（图３）。

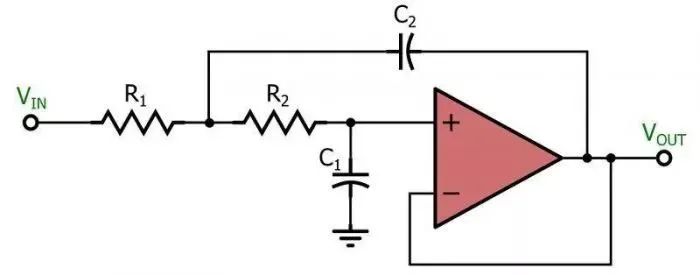
图3

这种有源低通滤波器基于流行的Sallen-Key拓扑结构。

本文将探讨无源低通滤波器的分析和设计。这些电路在各种系统和应用中发挥着重要作用。

RC低通滤波器

为了创建无源低通滤波器，我们需要将电阻元件与电抗元件组合在一起。换句话说，我们需要一个由电阻器和电容器或电感器组成的电路。从理论上讲，电阻—电感（RL）低通拓扑在滤波能力方面与电阻—电容（RC）低通拓扑相当。但实际上，电阻—电容方案更为常见，因此本文的其余部分将重点介绍RC低通滤波器（图４）。

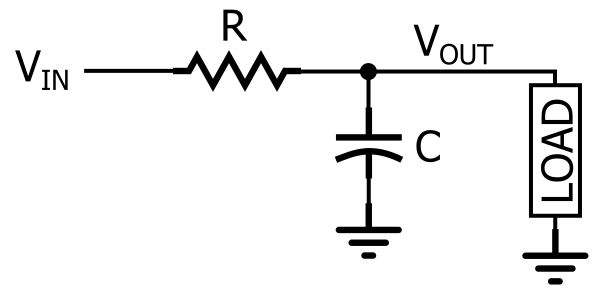
图4：RC低通滤波器

如图所示，通过将一个电阻与信号路径串联，并将一个电容与负载并联，可以产生RC低通响应。在图中，负载是单个组件，但在实际电路中，它可能更复杂，例如模数转换器，放大器或示波器的输入级，用于测量滤波器的响应。

如果我们认识到电阻器和电容器形成与频率相关的分压器，就可以直观地分析RC低通拓扑的滤波动作（图５）。

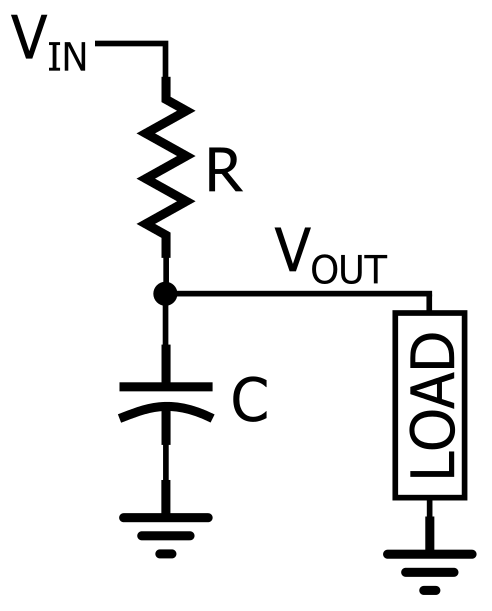
图5：重新绘制RC低通滤波器，使其看起来像分压器

当输入信号的频率低时，电容器的阻抗相对于电阻器的阻抗高；因此，大部分输入电压在电容器上（和负载两端，与电容器并联）下降。当输入频率较高时，电容器的阻抗相对于电阻器的阻抗较低，这意味着电阻器上的电压降低，并且较少的电压传输到负载。因此，低频通过并且高频被阻挡。

RC低通功能的这种定性解释是重要的第一步，但是当我们需要实际设计电路时它并不是很有用，因为术语“高频”和“低频”非常模糊。工程师需要创建通过并阻止特定频率的电路。例如，在上述音频系统中，我们希望保留5kHz信号并抑制500kHz信号。这意味着我们需要一个滤波器，从5kHz到500kHz之间的传递过渡到阻塞。

RC低通滤波器

滤波器不会引起显著衰减的频率范围称为通带，滤波器确实导致显着衰减的频率范围称为阻带。模拟滤波器，例如RC低通滤波器，总是从通带逐渐过渡到阻带。这意味着无法识别滤波器停止传递信号并开始阻塞信号的一个频率。然而，工程师需要一种方便，简洁地总结滤波器频率响应的方法，这就是截止频率概念发挥作用的地方。

当您查看RC滤波器的频率响应图时，您会注意到术语“截止频率”不是很准确。信号光谱被“切割”成两半的图像，其中一个被保留而其中一个被丢弃，不适用，因为随着频率从截止点下方移动到截止值以上，衰减逐渐增加。

RC低通滤波器的截止频率实际上是输入信号幅度降低3dB的频率（选择该值是因为幅度降低3dB对应于功率降低50％）。因此，截止频率也称为-3dB频率，实际上该名称更准确且信息量更大。术语带宽是指滤波器通带的宽度，在低通滤波器的情况下，带宽等于-3dB频率（如图６所示）。

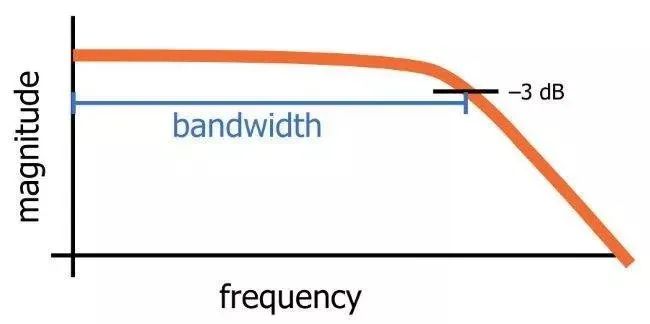
图6

图6表示RC低通滤波器的频率响应的一般特性，带宽等于-3dB频率。

如上所述，RC滤波器的低通行为是由电阻器的频率无关阻抗与电容器的频率相关阻抗之间的相互作用引起的。为了确定滤波器频率响应的细节，我们需要在数学上分析电阻（R）和电容（C）之间的关系，我们还可以操纵这些值，以设计满足精确规格的滤波器。RC低通滤波器的截止频率（fC）计算如下：

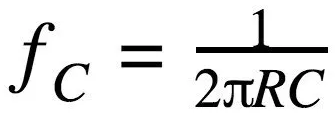
图7

我们来看一个简单的设计实例。电容值比电阻值更具限制性，因此我们将从常见的电容值（例如10nF）开始，然后我们将使用该公式来确定所需的电阻值。目标是设计一个滤波器，它将保留5kHz音频波形并抑制500kHz噪声波形。我们将尝试100kHz的截止频率，稍后在文章中我们将更仔细地分析此滤波器对两个频率分量的影响，公式如图8。

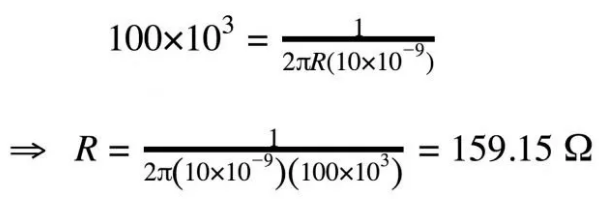
图8

因此，160Ω电阻与10nF电容相结合，将为我们提供一个非常接近所需频率响应的滤波器。

计算滤波器响应

我们可以通过使用典型分压器计算的频率相关版本来计算低通滤波器的理论行为。电阻分压器的输出表示如图9：

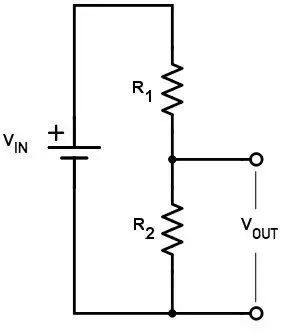
图9

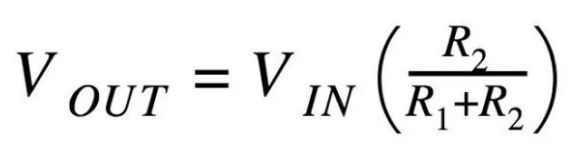
图10

RC滤波器使用等效结构，但是我们有一个电容器代替R2（图10）。首先，我们用电容器的电抗（XC）代替R2（在分子中）。接下来，我们需要计算总阻抗的大小并将其放在分母中。因此，我们有（图11）：

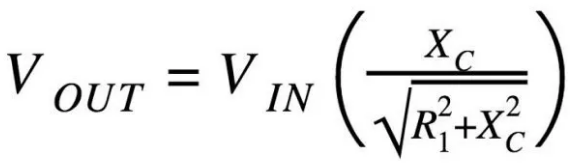
图11

电容器的电抗表示与电流的相反量，但与电阻不同，相反量取决于通过电容器的信号频率。因此，我们必须计算特定频率的电抗，计算公式如下（图12）：

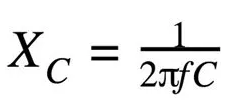
图12

在上面的设计实例中，R≈160Ω且C=10nF。我们假设VIN的幅度是1V，这样我们就可以简单地从计算中去掉VIN。首先让我们以正弦波频率计算VOUT的幅度（图12）：

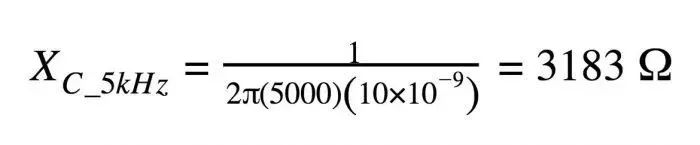
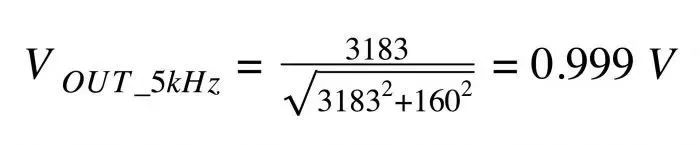
图13

正弦波的幅度基本不变。这很好，因为我们的目的是在抑制噪音的同时保持正弦波。这个结果并不令人惊讶，因为我们选择的截止频率（100kHz）远高于正弦波频率（5kHz）。

现在让我们看看滤波器如何成功衰减噪声分量（图14）。

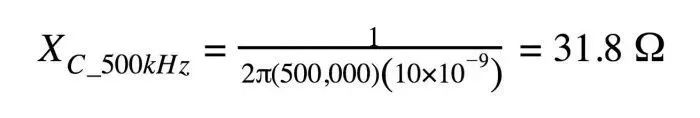
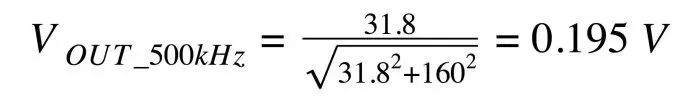
图14

噪声幅度仅为其原始值的约20％。

可视化滤波器响应

评估滤波器对信号影响的最方便方法是检查滤波器频率响应的图。这些图形通常称为波德图，在垂直轴上具有幅度（以分贝为单位），在水平轴上具有频率；水平轴通常具有对数标度，使得1Hz和10Hz之间的物理距离与10Hz和100Hz之间，100Hz和1kHz之间的物理距离相同等等（图15）。这种配置使我们能够快速准确地评估滤波器在很大频率范围内的行为。

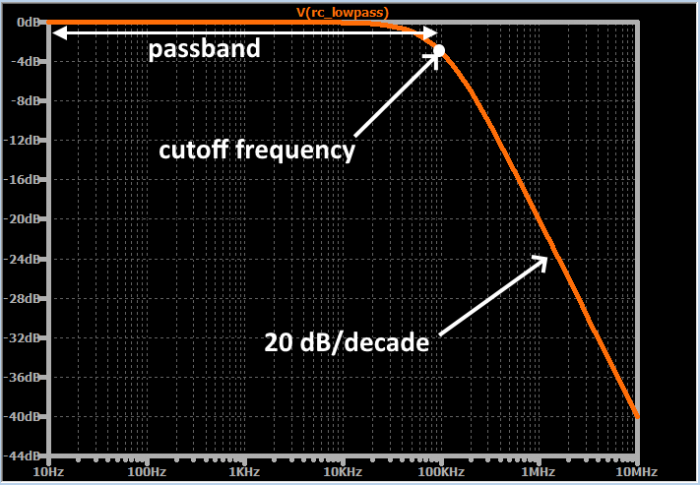
图15：频率响应图的一个例子

曲线上的每个点表示如果输入信号的幅度为1V且频率等于水平轴上的相应值，则输出信号将具有的幅度。例如，当输入频率为1MHz时，输出幅度（假设输入幅度为1V）将为0.1V（因为-20dB对应于十倍减少因子）。

当您花费更多时间使用滤波器电路时，此频率响应曲线的一般形状将变得非常熟悉。通带中的曲线几乎完全平坦，然后随着输入频率接近截止频率，它开始下降得更快。最终，衰减的变化率（称为滚降）稳定在20dB/decade-即，输入频率每增加十倍，输出信号的幅度降低20dB。

评估低通滤波器性能

如果我们仔细绘制我们在本文前面设计的滤波器的频率响应，我们将看到5kHz时的幅度响应基本上是0dB（即几乎为零衰减），500kHz时的幅度响应约为-14dB（对应于0.2的增益）。这些值与我们在上一节中执行的计算结果一致。

由于RC滤波器总是从通带到阻带逐渐过渡，并且因为衰减永远不会达到无穷大，我们无法设计出“完美”的滤波器—即对正弦波没有影响并完全消除噪声的滤波器。相反，我们总是需要权衡。如果我们将截止频率移近5kHz，我们将有更多的噪声衰减，但我们想要发送到扬声器的正弦波也会衰减更多。如果我们将截止频率移近500kHz，我们在正弦波频率下的衰减会减少，但噪声频率下的衰减也会减少。

低通滤波器相移

相位的概念是指周期内特定时刻的周期信号的值。因此，当我们说电路引起相移时，我们的意思是它会在输入信号和输出信号之间产生偏差：输入和输出信号不再在同一时刻开始和结束它们的周期。相移值（例如45°或90°）表示产生的偏差量。

电路中的每个电抗元件都会引入90°的相移，但这种相移不会同时发生。输出信号的相位与输出信号的振幅一样，随着输入频率的增加而逐渐变化。RC低通滤波器中有一个电抗元件（电容器），因而电路最终也会引入90°的相移。

与振幅响应一样，通过检查水平轴表示对数频率的曲线图，可以最容易地评估相位响应。以下描述表示了一般模式，查看图1可以进一步了解详细信息。

相移最初为0°。

相移逐渐增加，直到在截止频率处达到45°；在这部分响应期间，变化率逐渐增加。

在截止频率之后，相移继续增加，但变化率逐渐降低。

随着相移逐渐接近90°，变化率变得非常小。

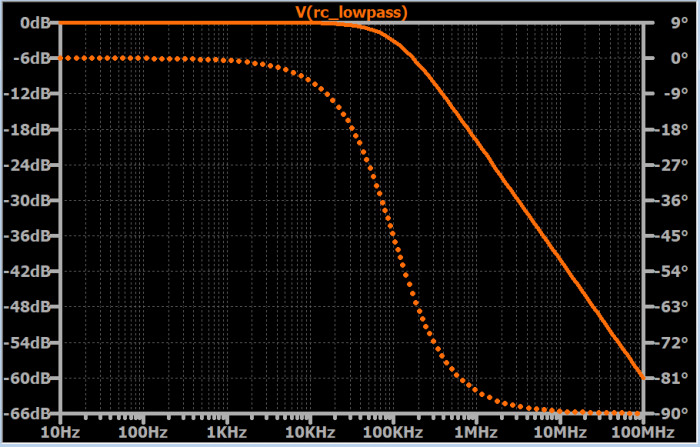
图1

实线是振幅响应，虚线是相位响应。截止频率为100kHz。注意，截止频率下的相移为45°。

二阶低通滤波器

到目前为止，我们假设RC低通滤波器由一个电阻器和一个电容器组成。这种配置是一阶滤波器。

无源滤波器的“阶数”由电路中电抗元件（即电容器或电感器）的数量决定。高阶滤波器具有更多的无功元件，会产生更多的相移和更陡的滚降，而后者是增加滤波器阶数的主要动机。

向滤波器添加一个电抗元件，例如，从一阶到二阶或二阶到三阶，便可将最大滚降增加20dB/十倍。

二阶滤波器通常围绕由电感器和电容器组成的谐振电路构建，这种拓扑结构称为RLC（Resistor-Inductor-Capacitor）。但是，也可以创建二阶RC滤波器。如下图所示，我们需要做的就是将两个一阶RC滤波器级联起来（图2）。

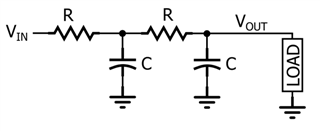
图2

虽然这种拓扑肯定会产生二阶响应，但它没有被广泛使用。正如我们将在下一节中看到的那样，其频率响应通常不如二阶有源滤波器或二阶RLC滤波器。

二阶RC滤波器的频率响应

我们可以尝试根据所需的截止频率设计一阶滤波器，然后从中选择两个串联连接来，从而构成二阶RC低通滤波器。此举确实可以使滤波器表示出类似的总频率响应，最大滚降为40dB/decade而不是20dB/decade。

但是，如果我们更仔细地观察响应，我们会发现-3dB频率出现降低。二阶RC滤波器的行为不符合预期，因为两个滤波阶段不是独立的，因此不能简单地将这两个滤波器连接在一起，并将电路分析为一阶低通滤波器叠加一个相同的一阶低通过滤。

此外，即使我们在两级之间插入缓冲器，使得第一阶RC和第二阶RC可以用作独立滤波器，此时原始截止频率处的衰减将是6dB而不是3dB。这恰恰是因为两阶独立工作而导致的。第一个滤波器在截止频率处具有3dB的衰减，而第二个滤波器加上了另外3dB的衰减（图3）。

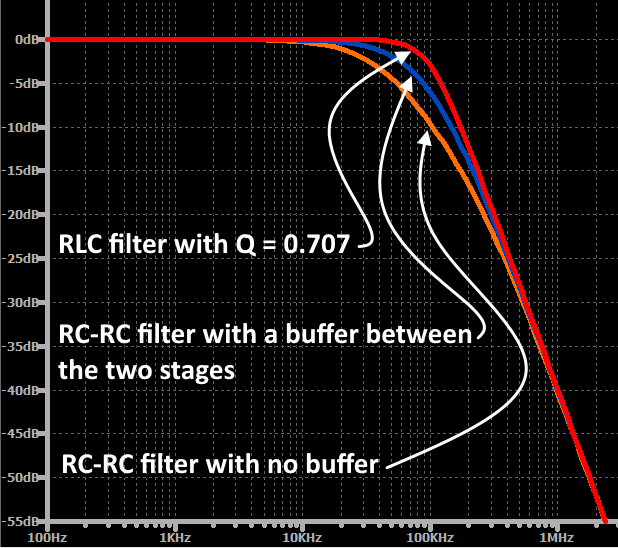
图3

二阶RC低通滤波器的基本限制是设计人员无法通过调整滤波器的Q因子来微调从通带到阻带的转换；此参数表示频率响应的阻尼程度。如果将两个相同的RC低通滤波器级联，则整体传递函数对应于二阶响应，但Q因子始终为0.5。当Q=0.5时，滤波器处于过阻尼的边界，这会导致频率响应在过渡区域中“下垂”。二阶有源滤波器和二阶谐振滤波器没有这一限制；设计人员可以控制Q因子，从而微调过渡区域的频率响应。

小结

所有电信号都混合了所需频率分量和不需要的频率分量。不需要的频率分量通常由噪声和干扰引起，并且在某些情况下会对系统的性能产生负面影响。

滤波器是以不同方式对信号频谱的不同部分作出反应的电路。低通滤波器旨在让低频分量通过，同时阻止高频分量。

低通滤波器的截止频率表示滤波器从低衰减变为显著衰减的频率区域。

RC低通滤波器的输出电压可以通过将电路视为由（频率无关）电阻和（频率相关）电抗组成的分压器来计算。

振幅（以dB为单位，在垂直轴上）与对数频率（以赫兹为单位，在水平轴上）的曲线图是检查滤波器理论行为的方便有效的方法，还可以使用相位与对数频率的关系图来确定将要应用于输入信号的相移量。

二阶滤波器的滚降更陡峭；当信号不能在所需频率分量和不需要的频率分量之间提供宽带分离时，这种二阶响应比较有用。

可以通过构建两个相同的一阶RC低通滤波器，然后将一个的输出连接到另一个的输入来创建二阶RC低通滤波器，但最终整体的-3dB频率将低于预期。

　　审核编辑：汤梓红