信号滤波降噪方法—小波滤波和EMD滤波

滤波是信号分析与处理中常用的一种手段，用以滤除信号中不需要的频率成分或提高信噪比。传统的滤波是在频域上实现的，通过对信号作Fourier变换得到信号的频域表示后，根据频率的分布情况，采用某种结构的滤波器按照一定的技术要求将欲去除的成分滤除。

然而，对于非线性和非平稳信号，频域滤波方法面临着很大的困难，因为利用Fourier变换很难得到这类信号的真实频谱，它们在频域上常常表现为许多的谐波成分，从而使得滤波后的信号失真。

现代滤波理论把信号和噪声都视为随机信号，利用它们的统计特征(如自相关函数、功率谱等)导出一套最佳的估值算法，从含有噪声的信号中估计出信号的某些特征或信号本身，以此来提高信号的信噪比。

维纳滤波法是现代滤波理论中的典型代表，其基本思想是在已知信号和噪声的相关函数或功率谱密度的条件下，通过求解积分方程，在最小均方误差意义上实现信号的最佳线性估计。

维纳滤波本质上是一种频域方法，只适用于单输入单输出的平稳随机信号，并且需要噪声和有用信号的先验知识，但是在实际中，这些先验知识很难得到或者过于简化，从而使得理论上最优的维纳滤波达不到要求。

（1）小波滤波

小波滤波是近十几年来小波变换在信号分析与处理领域中的一个重要应用方面，其基本原理是将含噪声的信号经过小波变换后，利用具体问题的先验知识，根据信号系数和噪声系数在不同尺度上具有不同性质的机理，构造相应的规则，在小波域对含噪信号的系数进行处理，目的在于减小甚至完全剔除噪声系数，同时最大限度地保留信号系数，得到真实信号的最优估计。

总的来说，小波滤波过程一般由三个步骤完成：小波变换、对小波系数非线性处理以滤除噪声和小波逆变换。

在对信号进行小波变换时，小波基的选取是一个非常关键的问题。理想的小波基应具有对称性、紧支撑，高消失矩和正交性，但要使一个小波基同时具有这些性质往往不现实，因此在应用中只能根据具体要求选择合适的小波基。

随着小波滤波理论研究的深入，若能做到按信号特征自适应选择小波基，则信号描述的效果将会得到较大的改善。

（2）EMD滤波

EMD将信号从高频至低频分解为若干阶IMF，整个过程体现了多尺度的滤波过程。借助这一点，我们可以方便地构造一种新型的滤波方式，即根据信号分析的目的，有选择性地把不同的IMF组合起来，以突出信号在某一频率范围内的特征。

显然，去掉先分解出来的几阶IMF，把其余的IMF和残余项组合起来，相当于原信号通过了一个低通滤波器；去掉最后分解出来的几阶IMF和残余项，把其余的IMF组合起来，相当于原信号通过了一个高通滤波器；去掉最先和最后分解出来的几阶IMF和残余项，只组合中间部分的IMF，相当于原信号通过了一个带通滤波器；去掉中间部分的IMF，将最先和最后分解出来的几阶IMF和残余项组合起来，相当于原信号通过了一个带阻滤波器。

这种基于EMD的滤波技术的优势是滤波后的结果能够充分保留信号的非线性和非平稳性信息，重新组合的信号不会对原信号的固有特性造成扭曲。

此外，由于EMD是依据信号的局部特征时间尺度分解的，是一种后验的分解方法，因此这种滤波方式自适应性较强，对信号类型几乎没有限制，不需要定义滤波器参数，受主观因素影响很小，是一种完全的数据驱动算法，简单易行，并且在多数情况下都可以达到满意的效果。

图1所示为含有高频衰减随机噪声干扰和低频趋势项的仿真信号，这是一个典型的非平稳信号，若用传统的滤波方法是很难将噪声和趋势项较好剔除的，而根据EMD的滤波特性对该信号进行滤波则可得到很好的效果。

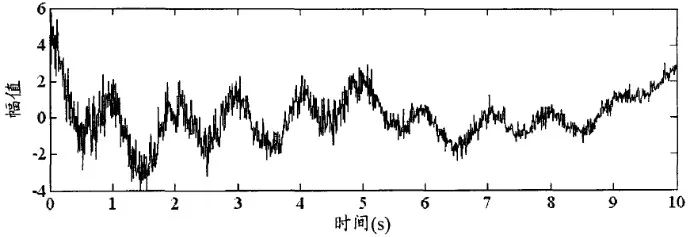
图1 含有高频衰减随机噪声和低频趋势项的信号

图2中的实线所示为利用该仿真信号的第七阶和第八阶IMF重构的结果，点线所示为相应的真实值，可以看到两条曲线非常接近。

图2 利用EMD滤波后的结果与真实值的比较