

机器人摆动相轨迹设计
描述
1、摆动相轨迹设计
基于第二节中提到的原则,文献[1]中提出了一种基于复合摆线形式的轨迹规划方法,并在文献[2]中得到了验证和使用。
针对机器人足底与地面接触时会产生滑动和行走过程中拖地问题,文献[2]对复合摆线规划方法提出了修改,修改后的摆动腿的步态规划轨迹定义为:
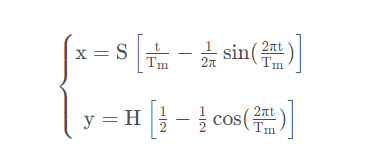
其中S为步幅, H为抬腿高度,T m 为摆动相周期现在我们来看提下它的图像,设定S = 100, H = 30, 周期T=2。
我们用python绘制该轨迹的图像如下:
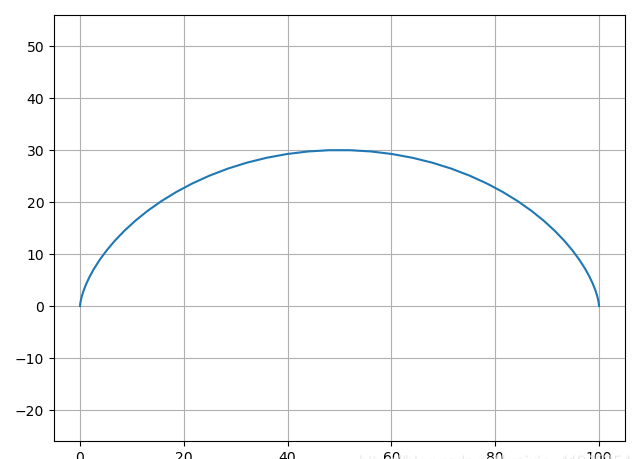
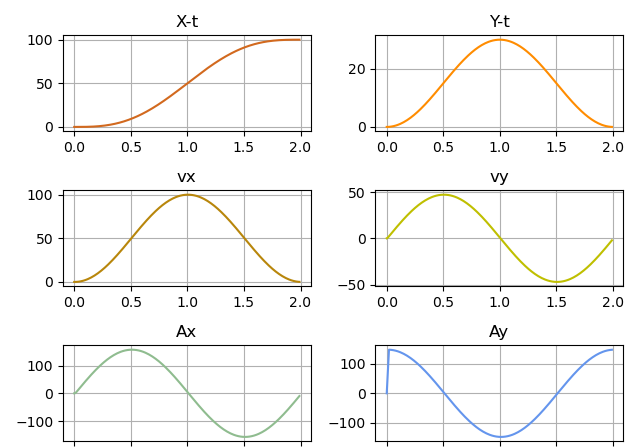
为了更好地研究该轨迹的特性,我们接下来依次看x,y关于时间的位置,速度,加速度
2、轨迹改进
从表达式上分析,该轨迹的加速度方程是余弦函数的倍数,在 t=0 和 t=Tm时刻会出现加速度跳变,根据F = M a
,这就导致了抬腿的瞬间要求产生较大的接触力。
从加速度图像亦能说明这一点。针对这一问题,文献[5]对 y 方向的位移方程提出了以下修改。
由于摆动腿在 y 轴运动需要先抬腿再落腿,借鉴 x 轴正弦方式运动的方法求解 y 轴位移曲线
先从加速度函数入手,我们设计成如下形式:
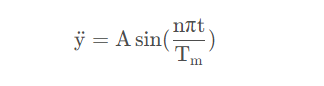
对上式进行积分求得速度函数:
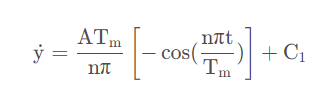
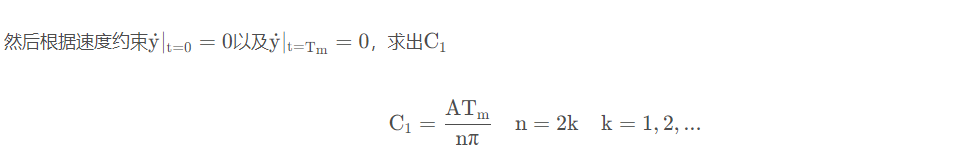
对速度函数进行积分,求得位移函数为:
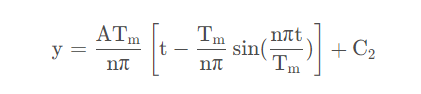

为了确定n的取值,我们来看看n取不同值时的速度图像,取T = 2 , H = 1 , S = 1
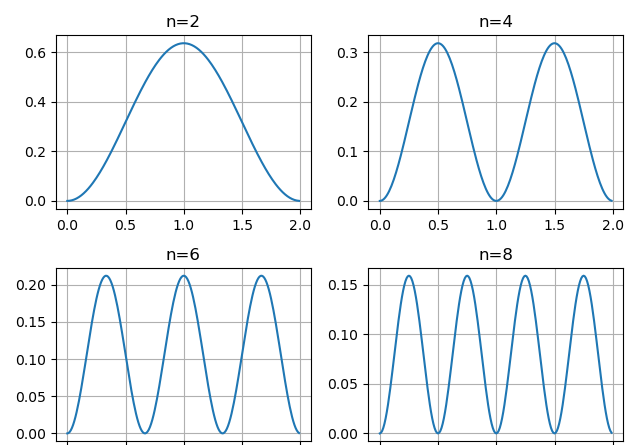
可以看出,当n越大时,y方向上的速度变化就越频繁,这可能会导致系统能耗的增加。
再来看位移图像:
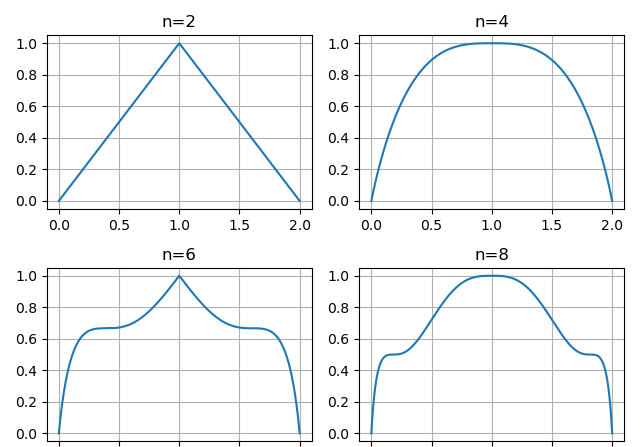
从位移图像来看,只有当n取4时,轨迹才是平滑的。因此我们可以确定轨迹的最终形式为:
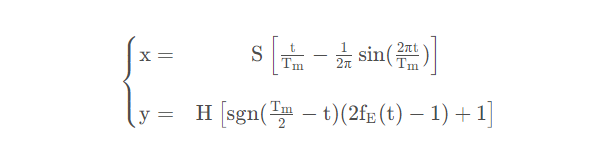
其中
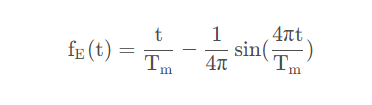
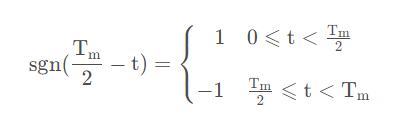
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
焊接机器人拖拽轨迹怎么设置2024-09-11 1165
-
机器人支撑相足端轨迹2023-11-22 1081
-
浅谈差速机器人的纯轨迹跟踪仿真2021-09-01 1488
-
机器人系统是什么?2019-09-10 3164
-
机器人基础书籍2019-05-22 3554
-
码垛机器人轨迹函数的优化2018-03-14 885
-
基于机器人的曲线焊接系统2018-03-13 5129
-
机器人的轨迹规划与生成2017-10-13 887
-
【机器人在线】喷涂机器人轨迹偏差优化的发展现状2017-07-12 3445
-
关节机器人控制2015-04-29 5166
-
机器人视觉——机器人的“眼睛”2015-01-23 6158
-
什么是工业机器人2015-01-19 6815
-
用labview能实现挖掘机机器人的轨迹规划吗?2013-04-01 3502
-
轨迹机器人教案2009-08-02 682
全部0条评论

快来发表一下你的评论吧 !

