

振荡器的工作原理解析
描述
在这篇文章中,我们将介绍振荡器(OSC)的工作原理。
在介绍锁相环中的压控振荡器之前,我们需要先对振荡器进行学习和理解。
振荡器是什么?顾名思义,就是通电后能自发发出周期性振荡信号的装置,我们不需要对这样的装置进行信号输入,只需要给装置接入电源就行。
从理论上来讲,振荡器的逻辑就是,系统中存在一个噪声(在物理专业里这样的信号叫做“涨落”),然后我们对其进行操作。所以在Cadence中模拟振荡器时我需要设立初值:设置初值方法
一般的振荡器都是如下两种原理:
- 系统选择某个特定频率的信号,对他不断地进行放大,而其他频率的信号则是一直是以噪声存在的小信号,于是输出了这个特定频率信号,由此产生特定频率的振荡信号。
- 系统中存在低频噪声,由于系统在信号传输的过程中存在延时,而且过了特定的时间后,这些信号会发现翻转,并且翻转信号会穿回最开始的器件装置,由此确定了系统每经过一个特定的时间信号就会发现翻转,且由于装置的MOS管存在寄生电容,装置的输出电压始终是连续地从0升到电源电压,或者是从电源电压降到0,由此实现了对输出信号频率地筛选,保证能输出特定频率的振荡信号。
1.三个反相器组成的振荡器
首先我们来理解如下图最直观的振荡器。这里我们的振荡器主干部分由三个反相器组成,后面的一个反相器是一个稳定输出信号的buffer。假设每一个反相器的延时是Ti,可以看到,当有一个噪声信号产生后,从最左端反相器输入到整个环路系统,可见信号经过三个反相器延时3Ti后会发生反相,信号有高电平翻转为低电平,或者由低电平翻转为高电平。通过振荡信号可见,每经过两次信号翻转,系统就经历了一个周期,由此产生了一个周期为6Ti的振荡信号。
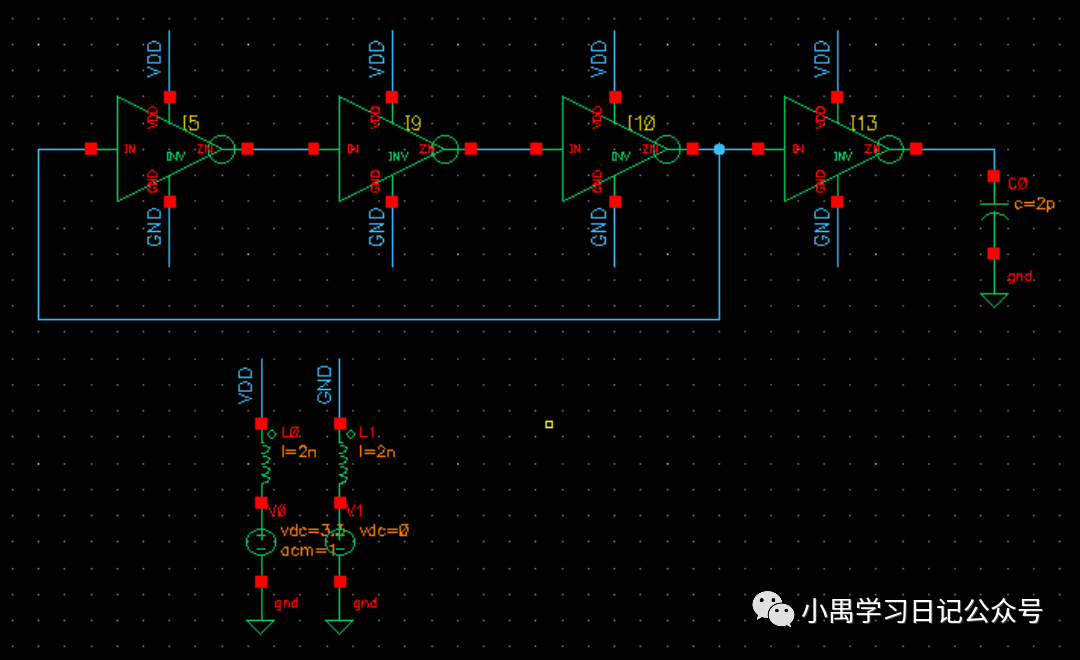
三个反相器组成的振荡器

仿真结果
不过这个建议装置很难设计出我们想要的频率的振荡信号,因为这个装置里的延时都来自于MOS管中的寄生电容。不过有个意思的事是,我们能看到每个周期的时长是0.3ns,那么就是说这里我们用到的MOS管的延时是0.05ns,由此每当我们遇到MOS管的时候也能估算一下系统的延时,这样的延时会直接影响到我们电子设备的处理数据、数据传输的速度。如果每个MOS都是固定的0.05ns,也就是说设备的频率最高达到20G,这可能就会成为硬件传输数据的速度极限(当然具体到信号传输的机制,可能还要考虑频分复用、时分复用等原理,速度会再快点)。
2.三级环形振荡器:共源级运放+RC
了解了三个反相器组成的振荡器,我们就能很容易地理解这一类振荡器了,它也是经过特定延时后,系统信号发生一次翻转,然后再传输回最开始的装置,由此循环往复。不过不同的是,在这里我们是用共源级运放实现信号翻转(信号反相),而且还加入了人为设定的RC电路来做延时,由此能保证输出振荡信号频率可控,我们就能设置输出特定频率信号的振荡器了。(RC电路的延时要求远大于MOS管内部的寄生电容带来的延时。) 通过模拟出来的振荡信号可见,振荡信号的周期在微妙量级,而上一个由三个反相器组成的振荡器的延时在纳秒量级。

三级环形振荡器:共源级运放+RC

仿真结果
3.运放+带通滤波器
在振荡器原理里,还有一条是:系统选择某个特定频率的信号,对他不断地进行放大,而其他频率的信号则是一直是以噪声存在的小信号,于是输出了这个特定频率信号,由此产生特定频率的振荡信号。下面我们来展示通过这个原理设计出来的振荡器。
如下图,左下角的1图,是一个带通滤波器,右上角2图是一个运放。通过电路分析可以看出,运放会把噪声方法,让后通过带通滤波器的选择后,只留下我们想要的频率的振荡信号,并且做输出。

运放+带通滤波器

仿真结果
由于运放并非理想运放,所以我在这里加了一个buffer。

buffer
4.交叉耦合 LC 振荡器
对LC振荡进行学习,我们会接触到石英晶振的等效电路图,品质因子Q因子,而且把这个电路中的电容器换成可变电容器,这个电路就会变成一个压控振荡器。
电感的 Q 值也叫作品质因数,其为无用功功率除以有用功功率。简单理解的话,就是在一个信号周期内,无用功功率为电感存储的能量,有用功功率为电感消耗的能量。电感在一个充放电周期内,储存并释放的能量为无用功能量,而因为这个过程额外损耗的能量就是有用功能量,损耗的能量主要作为热量耗散。在自谐振频率处,电感与其寄生电容谐振了,相当于一个电阻。或者从微观上看,进入电感的能量在其内部电容和电感中来回倒腾,并不能释放出来,只能通过 Rs 慢慢消耗掉,Q=0。Q 值越高,电感的性能越接近于理想的无损电感,这也说明了它在谐振电路中的选择性更好,因此,谐振电路要选择高 Q 值电感。

石英晶振等效电路图
大概原理就是每过一段时间信号翻转,且LC电路会对信号进行筛选,由此产生了振荡信号。我们能通过设计R,L,C的值来设置输出振荡信号的频率。这里面还有一个概念叫做负阻,是分析RLC电路用的一种理论,在这里就不做详细叙述了,可以参考学习拉扎维的模拟CMOS集成电路设计。

交叉耦合 LC 振荡器
不过在我实际模拟的过程中,使用工艺库中的电感,输出的信号都会是这种不断衰减的信号。

选择工艺库中的电感带来的输出信号
当我把电感换成理想电感时,才会输出特定频率的振荡信号。

选择理想电感带来的输出信号
窗口比较式振荡器
最后放一个我在文献上学来的一个振荡器,等到有时间后在对这个模型做详细讲解。为了讲清它我们需要使用到恒流源、电荷泵、迟滞比较器、寄存器等知识,这是一个综合性的话题,可以留到下下次再水一篇文章。

窗口比较式振荡器
-
压控振荡器的工作原理是什么2024-09-25 2188
-
多谐振荡器的工作原理、分类、设计方法和应用2024-07-17 5932
-
Colpitts振荡器的工作原理和主要特性2024-05-22 2525
-
振荡器的工作原理2023-07-04 3608
-
ZVS振荡器的工作原理及参数设计2022-08-24 9181
-
振荡器的分类及工作原理2021-08-11 19896
-
石英晶体振荡器工作原理和应用2017-02-07 1672
-
压控振荡器工作原理及应用2010-04-23 11040
-
RC桥式振荡器的工作原理2010-04-20 8147
-
压控振荡器(VCO)的定义 控振荡器工作原理及应用2010-04-17 7125
-
反馈式振荡器,反馈式振荡器工作原理分析2010-03-22 3177
-
振荡器工作原理2009-08-21 16954
-
变形间歇振荡器工作原理2008-01-21 1432
全部0条评论

快来发表一下你的评论吧 !

