RC复位电路原理分析

前几周逗比君在调试时遇到了这样一个现象，如下图所示

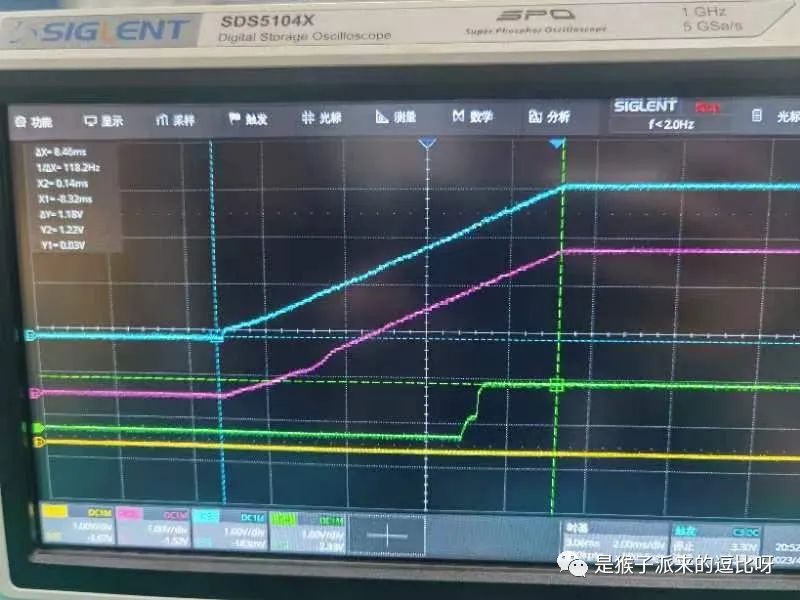
蓝色的是3.3V上电信号（除个别芯片使用其他电压外，整板使用3.3V供电），粉红色的复位信号（此处的复位信号是低电平有效的RC接反相器之后的输出），横轴每格为2ms，纵轴每格为1V。复位信号的产生使用RC上电复位，可是这里的上电复位信号竟然就这么随着3.3V 就这么头也不回的一起走了！其结果就是我的芯片并没有收到期望中的复位信号，导致工作异常。

于是，逗比君就决定好好理一理RC上电复位里的各种门道！

依据复位信号的分类，RC复位电路又可分为高电平有效的RC复位（下图左）和低电平有效的RC复位（下图右）

以低电平有效的RC复位电路为例，我们首先对其原理进行分析：

在0时刻，电容C两端电压为0，对应RST为低电平

在无穷远时刻，电容C两端电压与VCC两端电压一致，对应RST为高电平

由此可知，随着电容C两端的电压逐渐升高，RST对地的电压幅值也在升高，对于普通的芯片而言，其识别到的低电平与高电平也总是一个范围，因此在Vrst到达芯片复位管脚可识别到的高电平后，低电平有效的复位时间结束，此后该管脚均保持高点平状态。

为了验证上述的理论分析正确性，我们对C两端的电压值进行计算：

此时Uc的计算变成了一个关于Uc的一元微分方程组（我也没想到这个地方会扯到高数，我也是服了我自己），那么我们就解一下这个东西

可以看到上述得到结果，在t=0时，电容两端的电压为0，在t趋近于无穷大时，电容两端的电压为Vcc，这个结果与我们的理论分析结果是一致的。

理解了这个之后，我们开始对复位时间进行分析，由上述的推导可知复位时间为

假设电容充电至0.9Vcc时认为复位完成，那么可以计算得到需要的时间为

通常将RC的乘积称为时间常数，由此可计算得到对应电路中的RC值用于电路设计。

在实际的应用中，假设电源电压为3V，芯片的复位管脚在大于2V时通常会认为是高电平，此时计算时间可知，仅在一倍的时间常数下，即可实现低电平RC复位的目的。

RC复位的基本原理我们到这里就算是说明白了，可以设想到实际应用中，如果仅用RC复位的话，其效果应同本文开头图中看到的现象一样，复位信号随着电源建立的过程逐渐上升，这与我们通常理解的电平由0到1的跳变过程是不一样的，因此我们这里加入反相器，来实现一个更加“平滑”的复位信号。

先来看看包含反相器的RC复位电路

图中的复位信号仅反向一次，事实上在我们实际使用中，需要反向三次来实现与原信号的一致

因此以某款反相器为例，继续向后分析

在反相器电源电压为3.3V时，由其手册可知正跃变阈值电压约为1.0V~2.0V之间，即未到达正跃变阈值电压时，反相器输出的总是一个低电平，到达正跃变阈值电压后，反相器输出的总是一个高电平，这样即可得到一个“平滑”的低电平到高电平的复位信号。

（到这里我们从另一个角度去思考下，低电平有效的RC电路中，电容C由于其本生的充电过程，使得反相器先到达其3.3V的工作电压，在反相器正常工作后，开始监控复位管脚上电压值，到达正跃变阈值后，输出的电平由低电平到达高电平，最终实现复位功能。）

接着我们为了使低电平有效的RC复位电路具有更强的鲁棒性，我们加入二极管来增强其在放电阶段的速度

二极管的作用可以理解为在电源断电后，电容可通过二极管迅速放电，待下次电源上电时实现可靠的上电复位。这种情况通常出现在电源因某种干扰瞬间断电时，电容C不能迅速将电荷放掉，在电源恢复后无法进行完整的充电造成芯片没有复位，致使芯片异常。

到这里我觉得理论分析部分基本结束，继续我们的故障讨论，在本文开始的图中，选用的电阻值为330K，电容为0.0224uF，计算可知时间常数约在7ms左右，通过观察3.3V的建立时间约为8ms左右，使得我们怀疑上电时间过缓造成的电容C的充电过程过于缓慢，同时给到反相器正常工作时，复位管脚的电压已经大于2V，造成复位管脚输出总是为高电平，最终造成复位信号也在一直爬坡。

改进方法就是增长电容C的充电时间，我们将电容值扩大到0.1uF，将时间常数扩大到35ms左右，此时的状态如下图所示，横轴每格为5ms，纵轴每格为1V，复位信号状态有显著改善，产品对应芯片复位引脚工作正常。

说到这里，RC复位电路，你好像也没有那么烦了~