

振荡器原理详解(1)
描述
1. 振荡器原理
1.1 振荡条件
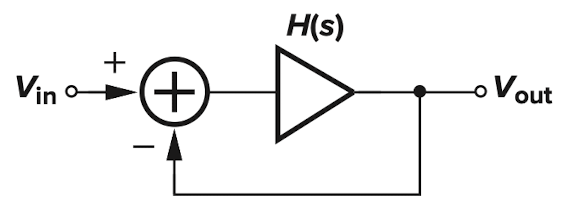
图一
对图一这样的闭环系统,要想实现振荡,最基本的就是要满足不稳定的条件,也就是巴克豪森准则:

其中ω0即为振荡频率。也就是说,在整个环路相移360°时幅值不小于1。

图二
假设H(s)为单极点系统,如图二。由于系统在DC情况下是负反馈,默认有180°相移,而单个极点最多贡献90°相移,加起来一共270°,达不到前面要求的360°,因而无法振荡。那么,假设我们串联两级作为H(s),如图三,会发现两个极点最多贡献180°,而现在在DC是正反馈,没有默认的相移,因此也无法达到360°,所以无法振荡。事实上,环形振荡器至少需要3个极点,如图四,三个极点一共可以贡献270°,加上负反馈的180°,足以达到振荡条件。

图三

图四
除了相位条件以外,还要满足相应的幅值条件。假设每一级极点相同,均为ω0,将图四的环路增益表达如下:

振荡时总相移360°,除了本身的负反馈180°以外,每一级贡献60°。可以计算得振荡频率ωosc和ω0的关系:


此时要求环路增益至少为1,可以求得对每一级低频增益的要求:


因此,每一级低频增益至少为2。
1.2 小信号与大信号
前面说了A0=2是保证振荡的基本条件,那么如果A0>2呢?为了方便理解,我们将图四的闭环传递函数推导如下:


有一个左半平面的闭环实极点,一对复极点。容易看出,A0=2时,这一对复极点位于虚轴上,处于临界稳定态;A0>2时,复极点位于右半平面,系统不稳定。这两种情况都可以保证振荡。忽略s1的影响,可以将时域表达式推导出来:

因此,A0>2时,指数项随时间增长而上升,最终趋于正无穷。这也说明系统是发散的,不稳定的。
事实上,由于电路的供电是一定的,振荡器的输出信号不可能真的到正无穷,最多只会饱和到电源电压。此时已经脱离了小信号的范畴,从大信号的角度分析,假设每级延时为TD,三级振荡器的振荡周期为6TD,频率为1/6TD。容易发现,这和前面的表达式里的频率A0*√3/2不同,一般会比它更低。

图五
怎么去理解这件事呢?如图五,假设一开始每级输出节点都处于中间电平,引入一点噪声之后每个节点开始逐渐振荡。一开始的幅度比较小,认为是小信号,振荡频率是A0*√3/2。随着幅度增长,电路逐渐脱离线性系统的范畴,振荡频率更接近大信号分析的1/6TD。最终振荡频率为1/6TD。
2. 电路实现
根据文章,早在1953年的真空管时代,一位叫Galley的前辈就提出了一个九级的环形振荡器专利,每一级本质上就是一个反相器。这种基于反相器的结构如图六。

图六
如前面所说,一共N级的话,振荡频率为1/(2NTD)。
除此之外,也可以用全差分的方式实现,如图七。

图七
由于篇幅所限,两种电路的具体分析与对比就留到下次再补充了。
-
皮尔斯振荡器的工作原理 皮尔斯振荡器电路详解2024-02-26 5634
-
MEMS振荡器与传统振荡器的比较2023-12-13 1159
-
什么是RC振荡器?RC振荡器的工作原理 基本RC振荡器电路设计2023-08-31 10303
-
一文详解振荡器2023-01-03 13382
-
详解多谐振荡器2019-06-04 3371
-
压控振荡器电路图大全(八款压控振荡器电路设计原理图详解)2018-03-02 93626
-
振荡器,振荡器的分类和原理是什么?2010-03-22 19485
-
振荡器,振荡器是什么意思2010-03-08 9860
-
振荡器工作原理2009-08-21 16954
-
反馈振荡器的原理2009-06-29 7525
-
无稳态多谐振荡器详解.ppt2007-06-15 3389
全部0条评论

快来发表一下你的评论吧 !

