LDO中使用cascode运放的补偿方法

上次讲了一篇文章里关于LDO的buffer设计的部分，那篇文章里还有很重要的一部分是讲如何在全负载范围内对LDO进行补偿，那么这次就继续总结一下。

1. LDO电路结构

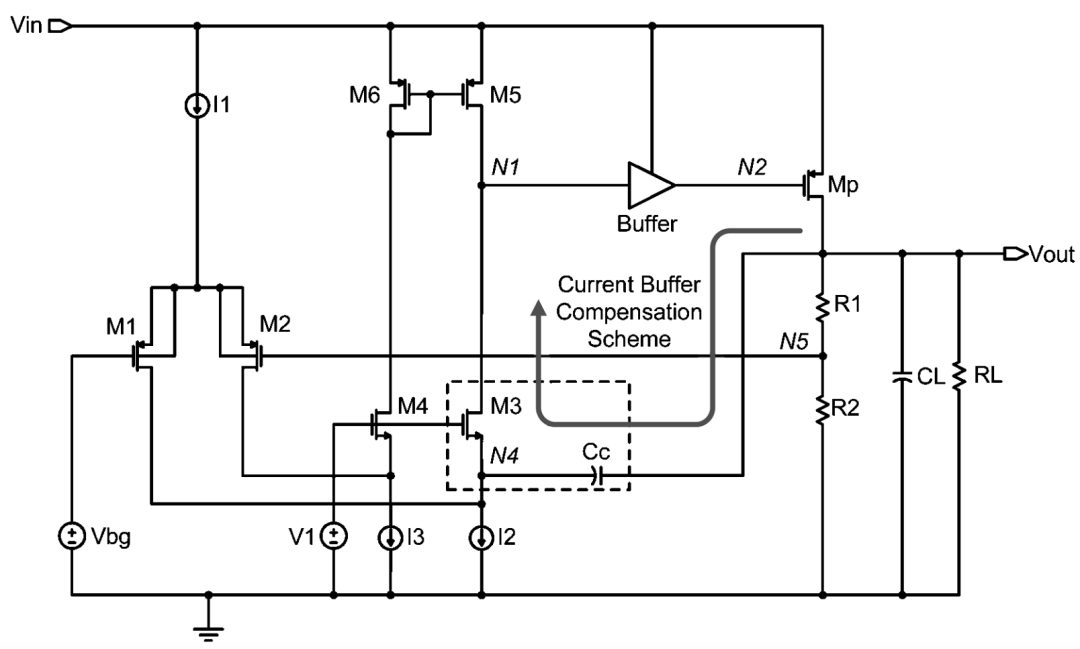
图一

我们先看看这个LDO的基本结构，如图一。这就是常规的一级folded cascode运放+一级buffer+一级pass device输出。正如我们上一篇文章所说，这个LDO的输出接了大的片外电容CL（比如1μF），所以主极点一直在输出端。重复一下我们遇到的稳定性问题： 在轻负载（IL接近0）时，输出电阻大，主极点低；重负载（IL接近LDO最大负载电流）时，输出电阻小，主极点高。 要保证全负载范围内的稳定性，之前我们设计了一个好的buffer，使N2电阻较小，将N2极点推到高频而可以忽略；在这基础上仍需增加一个补偿电容Cc（如图一），用于在某些负载情况下分裂主极点和次极点N1。

图二

将系统框图整理为图二。此处忽略N2处的极点，同时B=R2/(R1+R2)，为电阻串分压比，Roeq=rop||(R1+R2)||RL，为输出节点电阻。从图示处断开环路可以求得环路增益：

其中，我们认为Cc和CL都远大于C1。从表达式可以看出，系统存在三个极点（分母有s的三次方），一个左边平面零点gm3/Cc。接下来，我们可以具体分析不同负载下的零极点分布。

2. 数学分析

2.1 轻负载

在IL=0的时候，Mp的电流只有电阻串上的这部分，也就是Vout/(R1+R2)，通常非常小，比如1～3μA。此时gmp为最小值，为了化简表达式，认为CLRoeq>>gmpro1CcRoeq。则重新化简T(s)为：

可见，左半平面零点抵消了一个非主极点，最终系统简化为普通两阶系统。主极点和次主极点分别为：

容易发现， 此时Cc并未起到极点分裂的作用，主/次极点仍和未补偿时一样 。但由于此时输出电阻大，主极点本来就比较低频，仅靠系统自身即可保证稳定性。

2.2 重负载

随着IL逐渐增大，gmp增大，输出电阻减小。gmp正比于√IL，而rop正比于1/IL，所以总的开环增益正比于1/√IL，随着IL增大而减小。而输出端主极点正比于IL，随着IL增大而增大。 增益带宽积GBW或者单位增益带宽ωu正比于√IL，随着IL增大而增大。 实际上，对两阶系统来说，为了得到足够的phase margin，次主极点需要在ωu之外，并且距离ωu足够远。从这个角度来说，重负载的稳定性补偿会更加困难。

此时，为了简化表达式，认为CLRoeqCcRoeq，重新化简T(s)为：

神奇地发现左半平面零点又抵消了一个极点，系统还是一个双极点系统。主极点和次极点分别为：

p-3dB | IL>>0 =

*此时Cc的极点分裂作用体现了出来。前面说过，IL最大的时候ωu也会最大，容易算出，ωu,max=gm1/Cc。（这里认为B=1，系统为单位增益运放，此时环路增益最大，也是稳定性补偿最恶劣的情况）由前面表达式可以看出，随着电流增大，gmp增大，次极点变高，主极点变低，稳定性变好。*

3. 补偿电容设计

既然两种情况下都可以化简为两阶系统，那么我们就重新统一一下T(s)的表达式，从分子和分母上同时除去左半平面零点部分(1+sCc/gm3)：

这么做的原因主要是希望从全负载范围里找出phase margin (PM)最差的点，在电路设计上保证稳定性。phase margin通常由ωu和次主极点决定：

再用FPM表示次极点和ωu的比例，比例越大越稳定：

这里，ADC是指低频环路增益。依然令B=1，将FPM展开：

其中，只有gmp随负载电流变化而变化。那么，将FPM对gmp求导，令导数等于0，可以得到FPM和PM的最小值：

最终，得出我们关心的结论，Cc如何取值：

先给出我们可以接受的最小PM，带入等式可以得出Cc。容易看出，C1越小，Cc就可以越小，也就是说，接在N1节点的buffer需要输入电容小，这和我们上篇文章里的目标也是吻合的。

最后，贴两张图表示不同负载下的稳定性（这里不再展开说明）：

图三

图四

后记：

把电容接到cascode管源级和第二级输出端的补偿方法并不是这篇文章首次提出。在这之前，已经有很多前辈讲过这种补偿方法。但是，这篇文章是从LDO的角度，给出了电路设计的指导性分析，非常便于大家参考和实践。

另外，笔者最近也看了这种补偿方法起源的几篇文章，之后逐渐整理出来和大家分享。