模拟信号处理电路之运算放大器实现原理

介绍

运算放大器或“运算放大器”有 5 个主要连接：

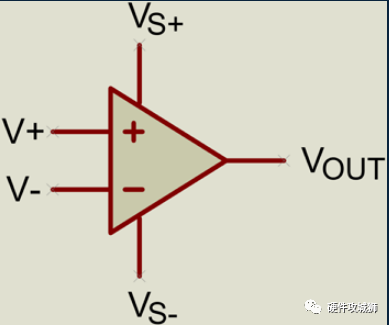
VS+ 和 VS- 称为电源轨，为运算放大器供电。从概念上讲，VOUT可以输出VS+和VS-之间任意电压；实际上，它被限制为略小于 VS+/大于 VS-，具体取决于特定的运算放大器和负载（从运算放大器汲取多少电流）。这是由于内部晶体管上的电压降造成的。

V+ 和 V- 是运算放大器的输入，并且是差分的，这意味着运算放大器根据这两个输入之间的值差进行工作。顾名思义，运算放大器在将差分输入传递到输出之前将其放大（倍增）。乘法值或增益非常高——大多数运算放大器约为 100,000 倍——但是可以使用一些技术使运算放大器具有更合理的增益（例如 2 倍或 10 倍），正如我们将在下面看到的部分。V+也称为同相输入，V-也称为反相输入。

比较器

比较器是一种比较两个模拟电压，然后根据电压较高者产生二进制数字输出（高或低、1 或 0、真或假）的设备。换句话说，比较器回答了以下问题：V+ 是否高于 V-？

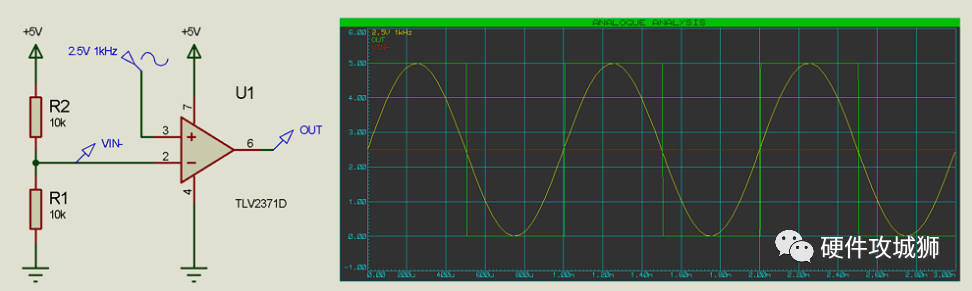
在上面的示例中，我们将运算放大器的正电源连接到 +5V，将负电源连接到 0V (GND)。V- 由分压器（电阻器 R1 和 R2）提供 +2.5V 参考电压。运算放大器提出这样的问题：V+ 是否大于 2.5V？

当 V+（黄色迹线）高于 2.5V（红色迹线）时，输出（绿色迹线）变高/真 (+5V)，当 V- 低于 2.5V 时，输出变低/假 (0V/GND) 。

通过改变 V- 的值，我们可以改变问题 – 例如，V+ 是否大于 1V？

缓冲区

运算放大器输入具有高阻抗，这意味着它们不会消耗相对较多的电流。当提供给运算放大器的源信号也是高阻抗时，这一点尤其重要，这意味着它不能提供太多电流，否则，当运算放大器或负载汲取的电流拉低电压时，信号会失真。

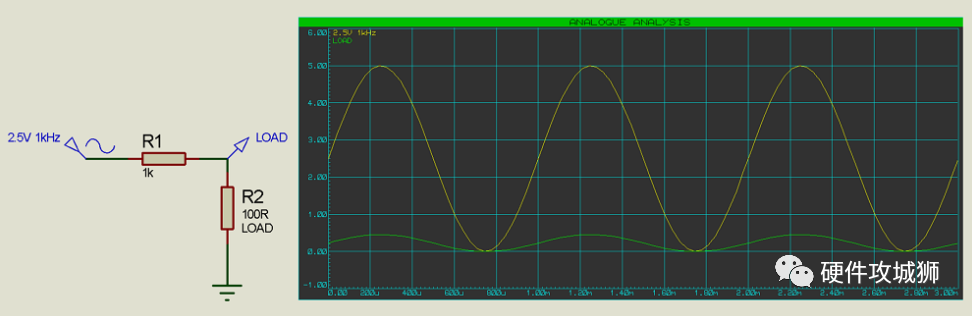
在上面的示例中，负载的输入是高阻抗的（1k 电阻限制可以提供的电流）。因此，信号（黄色迹线）在到达负载时严重失真（绿色迹线）。

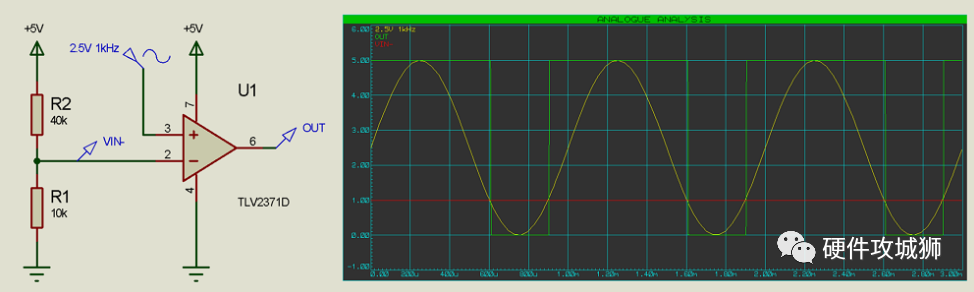
通过将运算放大器的输出反馈回 V-，我们可以为运算放大器提供 1（单位）的增益（乘数），并且运算放大器将从其电源轨（低阻抗）提供额外的电流。

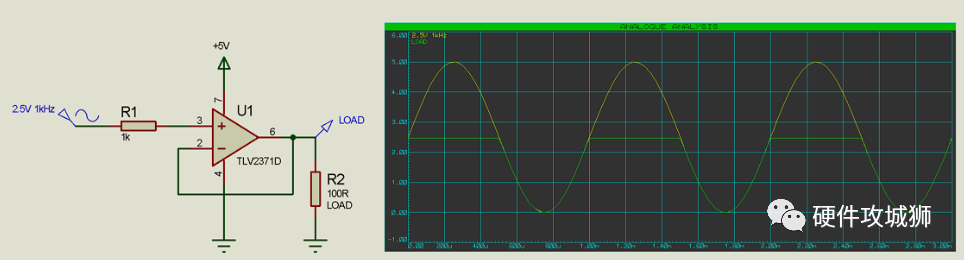
由于构成运算放大器的内部组件上存在压降，我们发现在该负载下，它可以在输出端提供最大约 2.5V 的电压，我们可以通过在正电源上为运算放大器提供 +9V 来解决这个问题:

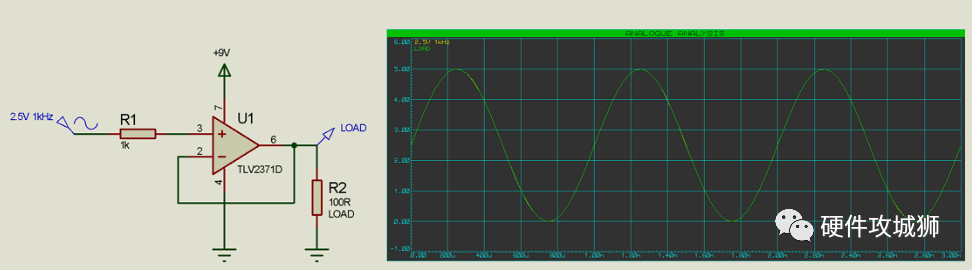
通过在缓冲器配置中使用运算放大器，并为其提供足够的功率/电压，我们可以将高阻抗源转换为低阻抗输出。

要了解缓冲区配置的工作机制，请考虑以下 3 个场景（请记住输出和 V- 是链接的）：

V+ > V-。运算放大器将差值倍增并增加输出电压，从而也增加 V- 处的电压并减小差分输入的大小。

V+ < V-。运算放大器将差值倍增并降低输出电压，从而也降低了 V- 处的电压，并再次减小了差分输入的大小。

V+=V-。运算放大器输出保持不变。

正差分输出

负差分输出

零差分输出

我们可以看到，运算放大器始终会调整输出/V-以减少差分输入，直到输出与V+输入匹配并稳定。另一个术语是输出跟踪 V+ 输入。

放大器

最后，我们讨论运算放大器的同名实现——实际放大。通过缩放 V- 输入的反馈，我们可以在输出上获得除 1 之外的增益（乘数）。

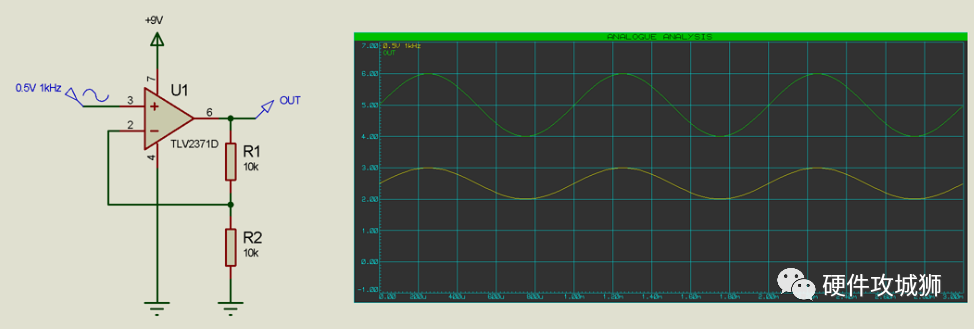
在上面的例子中，我们有一个以 2.5V 为中心的 0.5V 1kHz 正弦波输入。请注意，我们还再次向正极电源提供 +9V。分压器上有一个 1:1 的比率，反馈到 V- 输入，导致增益为 2。输出可能并不完全符合您的预期，因为它以 5V 为中心，但从技术上讲，这是正确 - 所有电压均已乘以 2。2.5V 中心变为 5V，3V 峰值变为 6V，2V 谷值变为 4V（2V-3V 之间的 1V 峰峰值幅度乘以 2V 峰峰值幅度在4V-6V之间）。

如果我们想选择 2.5V 作为放大的中心（或偏移）电压，那么我们必须将增益反馈参考为 +2.5V（如有必要，可能由单独的缓冲运算放大器提供）：

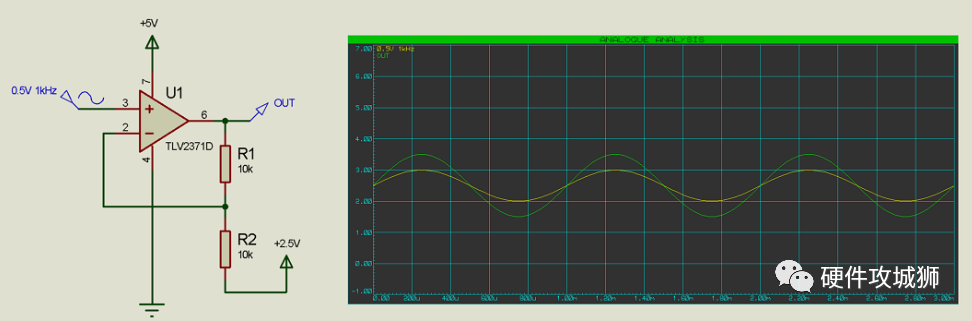
现在我们的峰值为 3.5V，谷值为 1.5V，这仍然给出 2V 的峰峰值幅度（因此增益为 2x）。

当然，我们还可以通过向运算放大器的负电源轨提供负电压（当然还向 V+ 输入提供以 0V 为中心的输入信号）来使输入和输出以 0V 为中心：

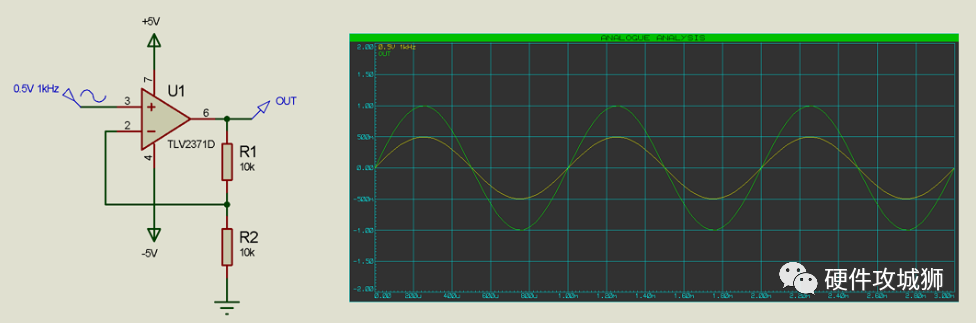
通过改变反馈分压器的比率，我们可以改变增益，例如下面的 3:1 分压器会产生 4 倍增益：

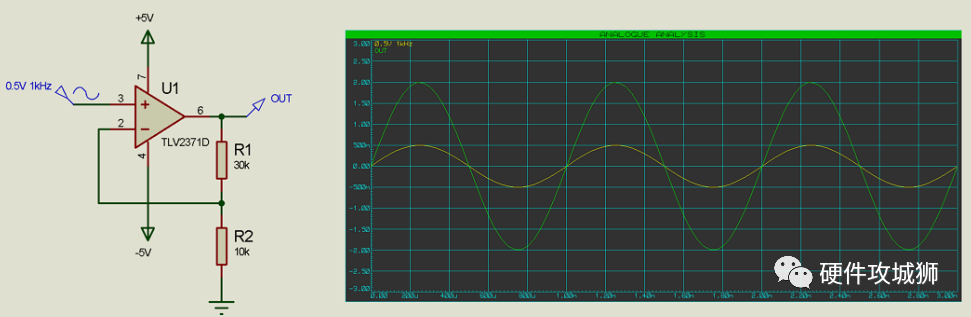
带迟滞的比较器（施密特触发器）

滞后现象可以描述为不愿改变。迟滞本质上是说，一旦我改变了，就需要一些说服才能让我再次改变。当输入徘徊在阈值附近时，这对于防止输出翻转（快速变化）非常有用。例如，我们可能有一个风扇，当温度高于 30°C 时，风扇就会打开；我们可能会发现，一旦风扇打开，温度就会降至 30°C 以下（例如 29.99°C），导致风扇再次关闭 – 一旦风扇关闭，温度就会回升再次升至30°C，风扇再次开启。这个循环可能会非常快速地重复，这可能会损坏风扇电机，并惹恼附近的任何人。向该系统添加迟滞意味着这样的说法：当温度达到 31°C 时风扇打开，但直到温度降至 29°C 以下之前它可能不会再次关闭。

通过将输出反馈回 V+ 输入，可以将迟滞添加到比较器运算放大器配置中：

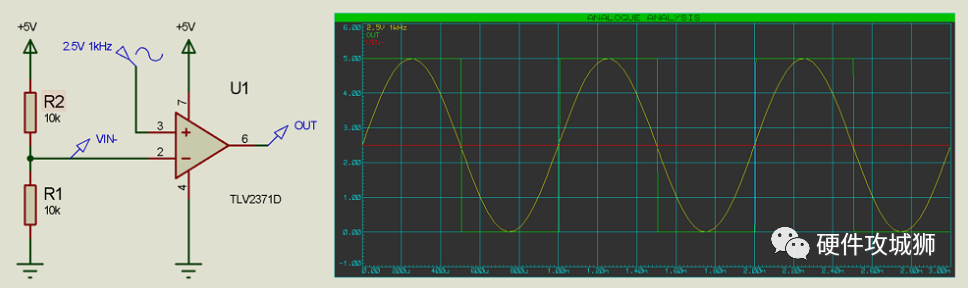
在这种情况下，我们可以看到输出在 2.5V 阈值之后犹豫不决，直到输入又超过它大约 1V。

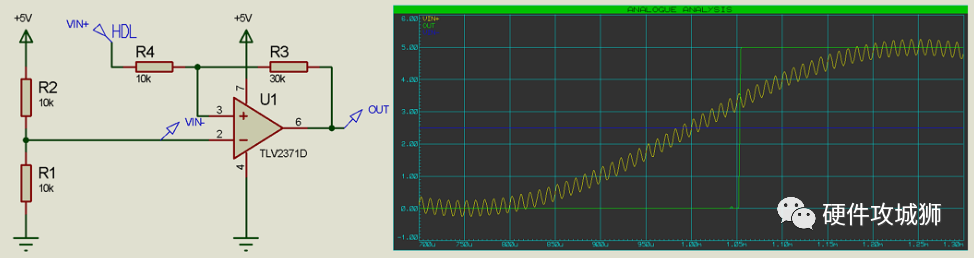
通过向输入添加一些噪声，我们可以看到滞后的用处：

在上述电路中，当噪声输入超过阈值时，输出会快速打开和关闭。

添加迟滞后，我们得到了一个干净的单开关：

运算放大器规格

当然，有许多不同型号的运算放大器可供选择，其规格和成本各不相同。一些规格包括运算放大器对输入变化的反应速度（带宽，这将决定运算放大器可以处理的最大频率）、运算放大器可以工作的最大电压、输出与电源电压的匹配程度（轨），运算放大器可以输出多少电流，等等；供应商网站上的参数搜索和数据表检查将有助于为特定应用选择正确的运算放大器。

结论

运算放大器是模拟信号处理电路中的重要组成部分，也可在数字应用中用作比较器。

审核编辑：黄飞