基于碰撞电离率的平行平面结及晶闸管研究

功率半导体器件设计的基础是平行平面结，结的击穿与体内载流子的碰撞电离密切相关，本次研究的重点结构是晶闸管，而晶闸管的阻断与开启都与体内载流子的运动有关。因此基于碰撞电离率的平行平面结及晶闸管的研究是很有必要的。

(1)应用简化的Fulop碰撞电离率模型对非穿通平行平面结耐压、峰值电场、导通电阻等与掺杂之间的关系进行计算。

(2)对更为准确的Chynoweth碰撞电离率模型进行化简计算。

(3)应用准确的Chynoweth碰撞电离率模型，基于已有的Miller公式，对不同漂移区掺杂浓度下的S参数进行了确定，提出了参数S与漂移区掺杂浓度N的拟合公式，并验证了其准确性。

(4)基于Chynoweth碰撞电离率模型对晶闸管的内部载流子运动及耐压机理进行计算仿真，应用MATLAB对提取的碰撞电离率进行验证。得到了较为准确的对晶闸管转折原因的解释。

非/穿通平行平面结的基本计算

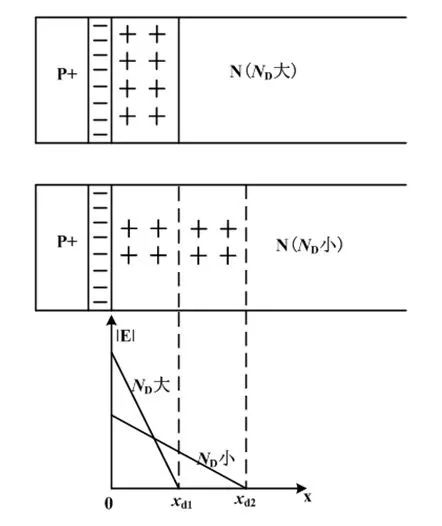
图1 在相同电压下势垒区厚度、杂质浓度与电场的关系

在设计器件时，耐压设计是很重要的一环。 这关系到耐压区掺杂，厚度等一系列问题。这些因素是通过影响耐压区电场来发挥作用的，而电场分布的变化又会影响碰撞电离率的大小。对于平行平面结的情形，耗尽层中的电势分布V(x)满足泊松方程：

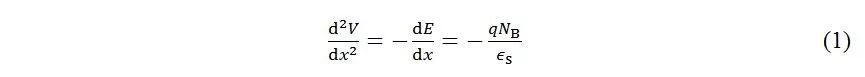
这里的q为基本电荷量，E为耗尽层中的电场，NB为掺杂浓度。由上式可得电场电势表达式：

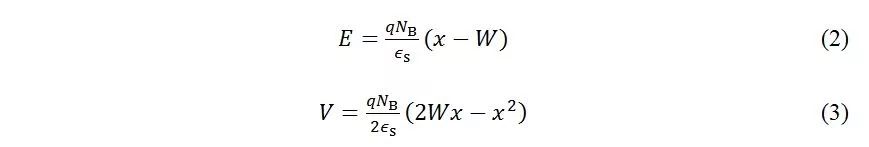
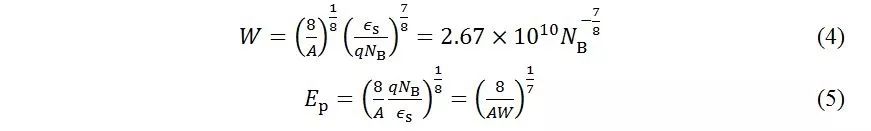
将4式与5式联立消去W，可以得到掺杂浓度与峰值电场的关系：

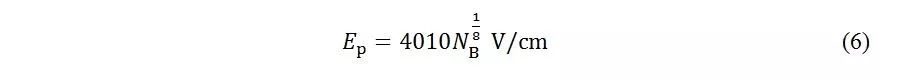
在单边突变结中，耗尽区的扩展与器件的掺杂有关，且根据电荷平衡原理，耗尽区主要向低掺杂一侧扩展。同时扩展宽度W与低掺杂的浓度有关。掺杂越低W越大。电场分布越不集中。因为反向电压与耗尽区宽度满足V =WE P /2的关系式。从而可得：

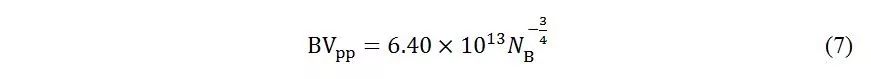
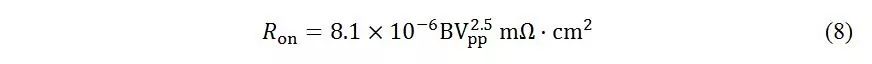
由V=WE P /2可知，电场在耗尽区里成三角形分布，三角形代表耗尽区宽度，高代表峰值电场E c ，轻掺杂情况下耗尽区宽度很大，峰值电场变小，要达到击穿，外加电压要加大。也就是说在低掺杂情况下击穿电压变大了。

从上面的计算可以看出对于非穿通平行平面结，掺杂浓度越低，结的耐压越高，二者存在着如式7所示的关系。电压的增加导致峰值电场的增加。峰值电场又与电离率积分密切相关。本节的计算应用的是误差较大的Fulop模型，但可以对结的耐压设计提供参考。后面将对更为准确的Chynoweth碰撞电离率模型进行化简，并为后续的计算提供依据。

碰/撞电离率积分的化简

碰撞电离（Ionization rate）是描述在强电场情况下，半导体内部载流子由于获得足够能量而碰撞激发产生倍增的一种现象。

高的外加电压，使半导体内部载流子加速运动获得了极大的动能。载流子之间相互碰撞，动能之间相互传递。当载流子获得的能量超过禁带宽度的能量Eg时，价电子会直接从价带跃迁至导带。电子成为自由的电子，同时产生相应的空穴。新产生的空穴电子对在强电场下又可以加速获得能量，继续进行晶格间的碰撞产生新的空穴电子对。

根据能量守恒定律可知这个激发能量大约为1.5倍的E g 。载流子的碰撞电离一直持续下去，势必会产生大量的空穴电子对，此时电流会急剧上升，也就是发生了雪崩倍增效应。

碰撞电离电子空穴对的产生率为：

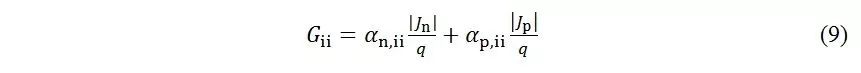
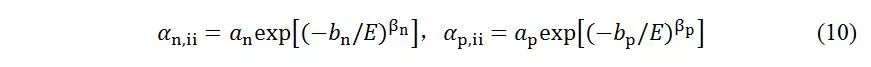
器件仿真中一般使用van Overstraeten的数据。

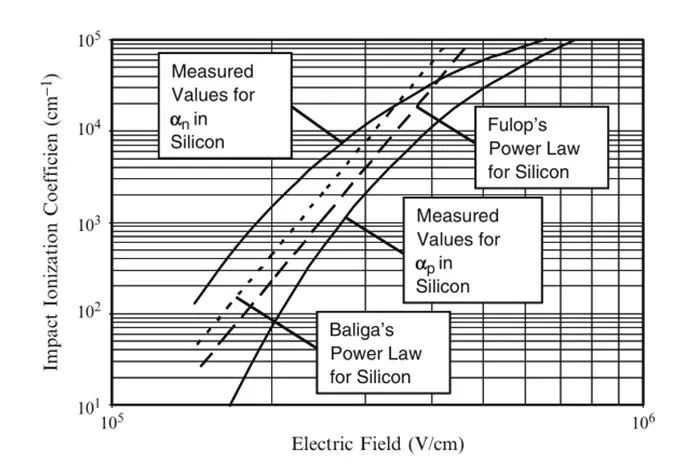
图2 硅中的碰撞电离系数

如图2所示，随着电场的增加碰撞电离率有一个快速的增长。当器件某一局部存在大的电场时此处电离率会很大，导致整体击穿电压的降低。

对于硅器件来说，电子的碰撞电离率是高于空穴的碰撞电离率的，因此对于器件耐压的判定一般是基于电子碰撞电离率来计算的。

碰撞电离是决定半导体器件的重要参数，在某些情况下需要器件发生碰撞电离来达到所需的高电流（如晶闸管、IMPATT二极管等）。而大多数情况下，要对它进行控制，以提高器件的耐压水平和防止有害的寄生效应。例如IGBT设计中，就不希望寄生晶闸管开启。

碰撞电离与器件的耐压水平息息相关，而表征器件发生击穿的方法就是对碰撞电离率进行积分处理，而模型的选择往往所得结果有所不同。相对于简单的Fulop模型，Chynoweth模型要复杂得多，在此模型下，PN结的雪崩击穿条件如式11所示。

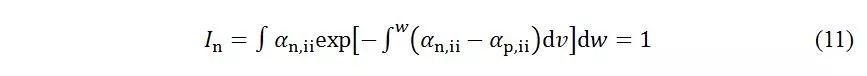
下面讨论关于碰撞电离率积分的化简的问题。

指数积分函数Ei(x)定义为：

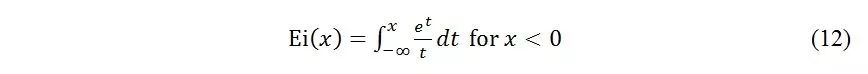
对于11中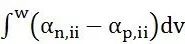定义为函数F(x)。

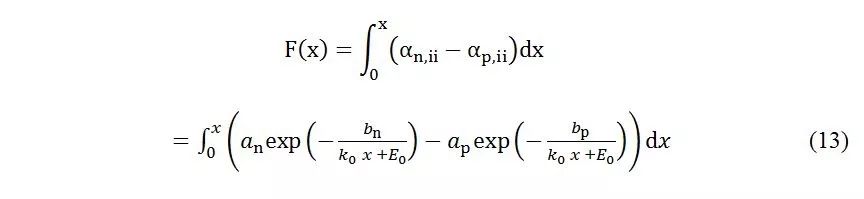
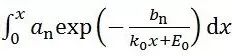
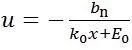当计算式13的第一个积分时，令，则

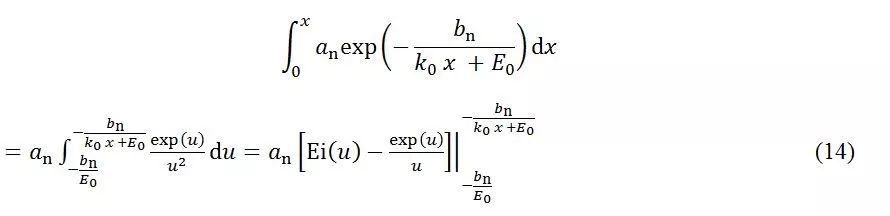
同理第二个积分也可得出，F(x)整理后便得到下面的表达式：

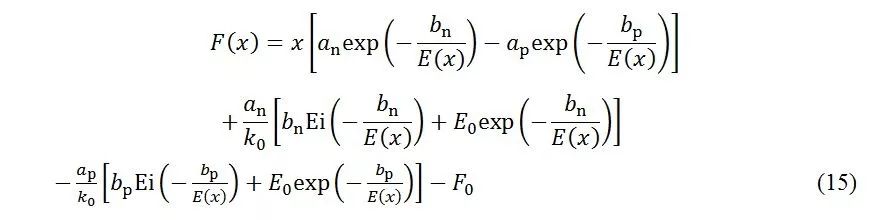
本节从最基本的非穿通PN结入手，分析了掺杂浓度与外加偏压，内部电场的关系。着重研究了Chynoweth碰撞电离率模型的化简。最终将二元积分方程简化为对一元积分方程的形式来求解。