带PID的数字输出控制示例解析

　　PID控制是一种算法，用于控制输出，以便将某个过程保持在精确值。一些例子包括：

　　控制船上的舵的位置以便驶向特定的方向。

　　控制提供给加热元件的功率，以保持特定的温度。

　　控制汽车的发动机油门以保持特定的速度（“巡航控制”）。

　　控制飞机副翼的位置以保持特定的旋转速度。

　　控制水处理厂中化学药品加入水流的速度。

　　PID有三个变量，即输入、输出和设定值。PID算法控制输出，以使输入与设定值相匹配。

　　例如，在控制船舵以驶向特定航向的场景中：

　　输入是指南针或GPS航向。

　　设定点是期望的航向。

　　输出是舵角。

　　输入和设定点之间的差异称为误差，PID算法旨在消除过程中的误差。为了理解为什么需要PID，让我们先来看看更简单的过程控制方法。

　　棒棒控制

　　Bang-bang控制是一种数字形式的控制，输出要么完全打开（最大值），要么完全关闭（最小值），两者之间没有任何东西。当输出也是数字时，这种控制似乎更直观；例如完全打开或关闭的阀门，或者可以打开或关闭的空调。使用空调的例子，输入将由温度传感器提供，并且设定点将是要保持的期望温度。算法很简单：

　　If the measured temperature is above the setpoint then we turn the air-conditioner on， otherwise we switch it off.对于某些应用程序，这可能工作得很好。然而，对于其他人来说，可能会遇到两个问题中的一个或两个：

　　设定点附近的读数快速变化。

　　第一个问题是在设定点附近相对快速波动的读数。例如，假设设定值为20 ℃，根据房间周围的气流或温度传感器的稳定性，读数可能在例如20.1℃和20.0℃之间波动；每次温度读数仅比设定值高0.1°C时，空调就会再次打开，一旦读数再次达到20.0°C时，空调就会再次关闭。这可能会很快发生，这既会让房间里的人感到讨厌，也可能会损坏空调。。如果制冷和制热都可用，我们可以想象一个场景，温度在19.9°C和20.1°C之间波动，空调和加热器相对快速地开关——两者互相干扰，浪费能源。

　　解决方案是在设定点附近增加一些延迟或缓冲，这称为滞后。在我们的例子中，2°C的滞后意味着一旦温度达到20°C并且空调关闭，那么空调不会再次打开，直到温度再次上升到22°C。如果也有暖气，那么在温度降到18°C之前，暖气不会打开（但是一旦打开，在温度升到20°C之前不会再次关闭）。

　　过冲。

　　可能遇到的第二个问题是超调。指令输出和输入测量输出指令结果之间存在延迟时，通常会出现过冲。以在水处理厂向水流中添加化学物质为例：化学物质需要一段时间才能溶解到水中，因此我们只能在添加化学物质的下游一点点处测量结果，也许是pH值，也就是说，在这个过程中会有一些延迟。比方说，我们开始时pH值有点太低，所以我们打开阀门向水中添加碱，以便使pH值升高一点；这开始起作用，但是当我们在传感器上读取pH中性值并关闭阀门时，大量的碱已经被添加到上游，传感器读数远远超过中性值，我们开始获得非常高的pH值读数；现在，系统通过打开阀门向水中添加酸来对高pH读数做出反应，以便再次降低pH值——但当这种影响到达传感器时，我们再次超过中性，读数再次变得过低……该过程重复，输出继续在设定点附近摆动——可能比触发纠正反应的原始误差幅度更大。

　　如果我们看看控制船舵位置或汽车发动机油门位置的例子，那么同样更直观明显的是，需要一个比bang-bang更好的控制系统——如果只需要一个小的航向修正，我们不想将船舵摆动到最右（右舷）或最左（左舷）;或者让汽车油门在踏板到金属和完全关闭之间摆动——我们需要介于两者之间的东西。

　　比例控制

　　比例控制（PID中的P）只做它所说的，并且控制输出与输入和设定点之间的差值成比例（与误差成比例）。如果输入和设定值之间的差异很小，那么我们仅对输出进行小的调整，如果差异很大，那么我们对输出进行大的调整。如果船只是稍微偏离了航向，那么我们只是稍微转动一下方向舵——我们不会把它转到底。对于某些系统来说，比例控制可能就是所需要的。然而，对于其他系统，会遇到下一种问题：

　　积分

　　使用比例控制时，几乎总是会有一定程度的稳态误差，这意味着系统不会完全达到设定值，因为接近设定值的比例控制量太小，不足以克服影响系统的某些偏差（可能是电流或风）。在下图中，过程稳定在设定值以下一点。

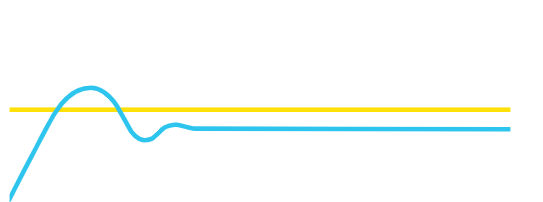
　　PID的积分（I）部分查看系统偏离设定值多长时间，并提升输出以克服该偏差。例如，如果汽车上的巡航控制设置为60英里/小时，但仅使用比例控制时，速度停留在57英里/小时（由于空气或其他阻力），那么PID的“积分”部分将随着时间的推移增加发动机功率，以使速度达到60英里/小时的设置。同样，对于某些控制器来说，PI控制可能就是全部所需。然而，在稳定之前，PI本身倾向于在设定点附近至少有一些过冲和振荡，特别是当设定点和输入读数之间存在大的初始差异时（例如在启动时或当对设定点进行大的调整时），因为PID的积分部分将在过渡期间累积所有的误差，并因此变大（比需要的更大），并且没有任何其他东西来抑制它，那么将再次减小它的唯一事情将是在相反方向上的一些累积误差。PID的D部分解决了这个问题：

　　导数

　　微分（PID中的D）元件通过根据其接近设定值的速度来缓和/抑制输出，从而最小化或消除过冲；如果输入读数非常快地向设定值移动，那么PID的微分部分将促使输出变缓，以便最小化或消除过冲。在数学中，曲线的导数是曲线在特定点的角度或梯度，即变化率，这就是这个术语的含义。在下图中，红线代表陡峭的梯度（这将导致PID算法中的大D校正），蓝线代表浅梯度（这将导致PID算法中的小D校正）。

　　调谐

　　PID算法中的每个元素——比例元素、积分元素和微分元素——都可以调整或加权，使其在算法中产生更大或更小的影响，正确的值因应用而异。PID调节是一个很深的主题，其全部深度超出了本文的范围，但是很好地理解P、I和D中每个元素的作用是一个很好的起点。选项包括为特定类型的流程、手动调整和模拟查找一些默认值。

　　手动调谐主要包括按顺序调谐P、I和D元件：

　　首先，I和D权重设置为零，P权重增加，直到系统开始在设定点附近振荡。然后，P权重被设置为该值的一半。

　　接下来，增加I权重，直到任何稳态误差被足够快地校正，但是不要太多以至于系统变得不稳定。

　　最后，增加D权重，直到任何过冲都被充分抑制，但没有抑制到系统响应迟缓甚至变得不稳定（尤其是在输入中有一些噪声的情况下会发生这种情况）。

　　带PID的数字输出控制

　　如果PID控制的输出是数字的，例如继电器或电磁阀，则可以使用脉宽调制等技术将数字输出有效地转换为模拟输出。PWM频率根据应用来选择，并且取决于系统，可以实施额外的约束，例如仅在占空比高于特定水平时才切换输出。

　　这是一个使用PICCOLO微控制器的烤箱PID控制示例，在中模拟变形VSM.

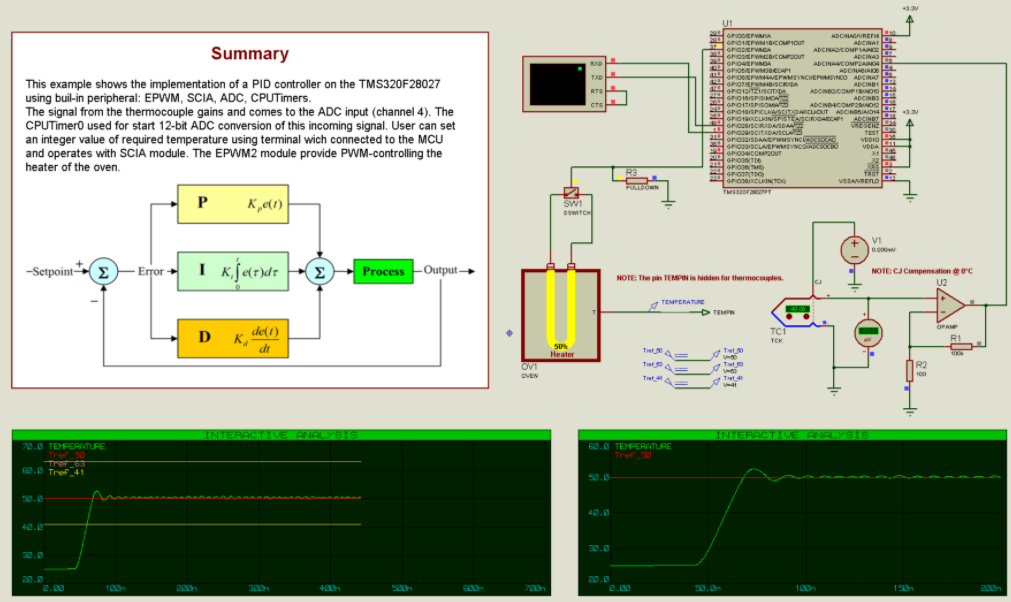
　　审核编辑：黄飞