用于微结构建模的NCM523正极三维重构及量化表征

用于微结构建模的NCM523正极三维重构及量化表征

背景介绍

锂离子电池作为电动汽车的主要动力来源，已经取得了长足的发展，其能量密度大幅增加。然而，要大规模全面替代传统燃油车，仍需要确保锂离子电池的高安全性、长循环寿命和快充能力。正负极作为电池的关键部件，其结构设计对电池性能影响很大。在电池厂中，电极开发通常采用反复试错的方法，即制造出具有不同结构的电极，然后采用一系列电化学测试方法对它们的性能进行评估。基于此，电池厂可以建立电极结构和电池性能之间的映射关系，并能够基于特定的需求来设计电池。这种方法虽然很可靠、直观，但是往往需要耗费大量的人力和物力。因此，一些研究尝试通过仿真的方法来优化电极结构。

最常用的模型是Doyle和Newman提出的伪二维（P2D）电化学模型。该模型基于多孔电极理论和浓溶液理论，通过求解一系列的偏微分方程来获得电池的内特性和外特性。许多研究人员使用该模型优化了电极结构，例如孔隙度、极片厚度和电池长宽比。这些优化使得电池的能量密度和功率密度显著提高。然而需要注意的是，P2D模型将电极颗粒假设为均匀分布的球体，因此该模型无法解析电极颗粒尺度上错综复杂的微结构。

事实上，电极的微结构对电池性能至关重要，尤其是寿命和安全性能。活性颗粒和孔隙的异质性分布会导致非均匀锂化状态和“热点”的形成，锂枝晶可能会在这些“热点”迅速生长，最终引起严重的容量衰减和安全问题。因此，必须对电极微结构进行解析，建立介观（颗粒）尺度的电池模型，并揭示电极微结构和电池性能之间的映射关系。

基于微结构建模的第一步，也是最关键的一步就是电极结构的三维重构。目前已经有很多种数值方法用于重建随机的电极结构，包括高斯随机场法、模拟退火法、基于过程的重建和随机网格法等。虽然这些方法具有简单、便捷的优点，但是随机重建的结构往往依赖于球体和椭圆体等标准形状。这种对电极颗粒形貌的简化和平滑处理无法准确捕捉真实的微结构特征，因此具有很大的局限性。所以通过基于图像的方法来获取电极微结构至关重要。

本文通过聚焦离子束扫描电子显微镜（FIB-SEM）获得了NCM523正极的二维图像集，然后通过图像处理的方法将其重建为三维结构并对电极的关键结构参数进行了量化，揭示了电极内部结构的异质性。

实施过程

2.1 样品准备和FIB-SEM测试

这项工作中使用的电极样品来源于一个1 Ah的商用软包电池。干电池在通过注液和化成步骤后，在手套箱中被拆解，其中正极被裁剪为一个很小的体积。随后将其封装在铝塑膜中并抽真空，以防止被空气氧化。

二维图像集是通过FIB-SEM来获得的，工作原理如图1所示。通过离子柱铣削从暴露的表面向内部去除薄层材料，然后对每个新暴露的表面进行成像。因此，可以获得一系列对比度良好的连续SEM图像，为三维重建提供输入。

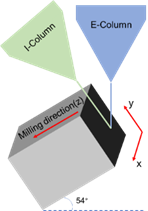
图1 FIB-SEM工作原理

2.2 图像处理和三维重建

由于FIB-SEM仪器本身的限制，只能在电子柱成像平面上获得清晰的图像，而在其他两个平面上都会观察到图像有偏移。在这里，我们采用中值滤波器来平滑三个平面上的图像，消除图像噪声和位移问题。中值滤波后的图像如图2d-2f所示，三个平面上的图像质量基本一致，并且都表现出较高的清晰度。

图2 滤波前后图像对比

电极包含三个不同的相：活性颗粒（AM）、导电剂-粘结剂（CBD）和孔隙（Pore）。为了分别研究各相的结构，采用了基于灰度值的交互式阈值分割方法，如图3a-3c所示。然后对三个相进行三维重构，结果如图3d-3f所示。此外，如图3g所示，这些分割的相还可以再无缝组合，并使用三种不用的颜色进行描绘。

图3 对三个相的分割和三维重构

2.3 关键结构量化表征

活性颗粒、导电剂-粘结剂和孔隙的体积分数是电极的基本几何特征，对于理解和模拟电极行为至关重要。因此，需要从重建的三维结构中精确计算出它们的体积分数，以便深入了解这些项在电极中的组成和分布。此外，活性颗粒的尺寸和形态对固液相界面的动力学反应和颗粒内的锂扩散过程具有重要影响；孔隙的连通性和迂曲度也会影响到锂离子在电解质中的传输。因此，必须分别对这两个相进行定量分析。

结果和讨论

3.1 体积分数和逐层面积占比

图4描述了三个相的体积分数和逐层面积占比在电极厚度方向上的分布情况。从体积分数中可以看出，活性颗粒作为主要的电极成分，占总体积的近70%；作为锂离子传输通道的孔隙也占了相当大的比例，约为23%；相比之下，作为添加剂的导电剂-粘结剂仅占总体积的8%左右。

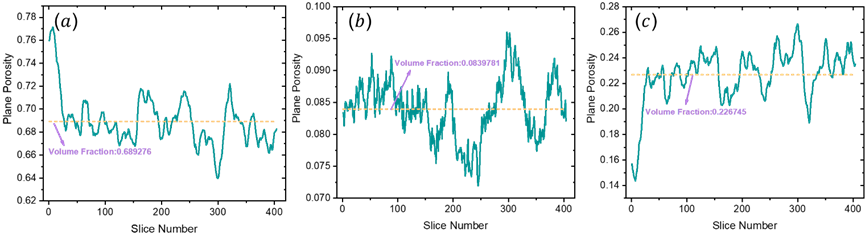
图4 三个相的体积分数和逐层面积占比

图四中切片数的增加表示切片位置逐渐从隔膜移动到集流体。从逐层面积占比中可以看出，从隔膜到集流体，三个相的平面占比在其体积分数附近上下波动。值得注意的是，在隔膜附近，活性颗粒的平面占比明显超过其体积分数，而孔隙的平面占比则明显低于其体积分数，这一结果表明活性颗粒在隔膜附近区域占主导地位。

3.2 活性颗粒的等效半径和球度

对于活性颗粒的分析流程如图5所示，从图5a中可以看出，由于交互式阈值分割中的误差，会导致很多本应分离的颗粒连接在一起，这些小颗粒很容易被误认为是一个完整的大颗粒。为了纠正这一错误，我们采用了一些算法对其进行分割。此外，从5c中可以看出立方体的边缘存在一些不完整的粒子，这些粒子也不是我们想要研究的对象，所以也需要予以清楚。最后的结构如图5d所示。

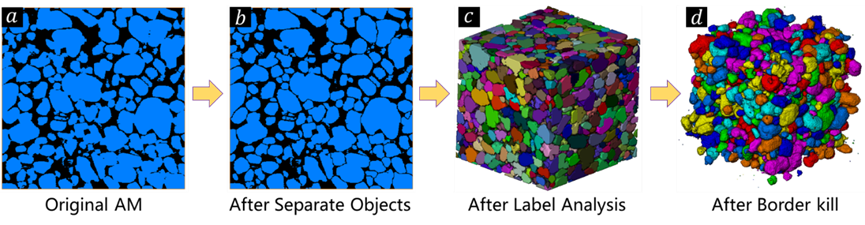
图5 活性颗粒分析的工作流程

如图6所示，通过分析图5d中每个颗粒尺寸和形态，可以得到每个颗粒的等效直径和球度。从图a中可以看出，颗粒尺寸在电极厚度方向上的分布大致均匀，然而，在每个横截面内，颗粒尺寸存在明显的异质性。最大的颗粒的等效直径可达6微米，而最小颗粒的等效直径甚至小于1微米。

图6b显示了这些粒子的球度分布，球度接近1表示粒子趋近于一个完美的球体。在本工作中，这个标准被放宽了，球度值在0.9-1.1之间的颗粒都会被视为标准球体。然而，从图6b中可以看到，只有33%的粒子满足之一标准。这进一步表明在P2D模型中将所有粒子都假设为球体是不合适的。

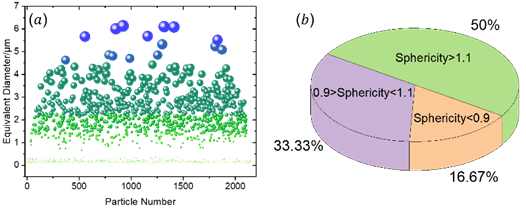
图6 活性颗粒的等效直径和球度分布

3.3 孔隙的连通性和迂曲度

孔隙可以被分为两类：连通孔隙和孤立孔隙。电解质只能在连通的孔隙内流动，进行电荷转移和离子扩散，因此，孔隙的连通性至关重要。从图7a-7c中可以看出，电极内只有一些很小的孤立孔隙，这个对电池性能的影响很小。

迂曲度也是表征多孔介质中孔隙形态的一个关键参数，其定义为渗流通道的实际长度与其直线长度的比值。迂曲度越高，意味着电极的渗透性越低，锂离子的传输路径越长，不利于电池的倍率性能。如图7d所示，可以通过将连通孔转化为骨架模型来计算每个分段通道的迂曲度。

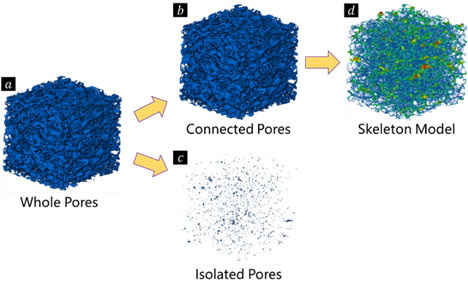
图7 孔隙连通性分析和骨架模型

迂曲度的计算结果如图8所示。可以看出，大多数分段通道的迂曲度在1-1.1之间，这反映出电解质的渗透性很好，电池具有良好的倍率性能。此外，与颗粒大小和形状的分布类似，电极内孔隙迂曲度的分布也是不均匀的。这一结果也强调了有必要对P2D模型进行调整，以便更好的捕捉真实电极内部的异质性。

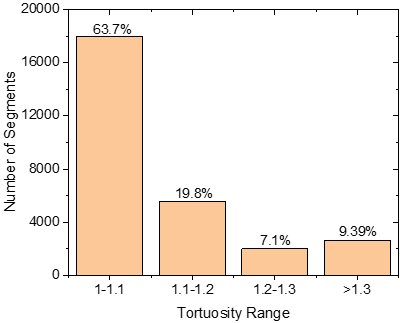
图8 孔隙内分段通道迂曲度的分布

审核编辑：刘清