

IGBT中的PIN结构分析(1)
电子说
描述
IGBT的结构中绝大部分区域是低掺杂浓度的N型漂移区,其浓度远远低于P型区,当IGBT栅极施加正向电压使得器件开启后,集电极、漂移区以及发射极(通过沟道,后文在MOS沟道效应时再详细讨论开启过程)会形成一个PIN结构,其中I是intrinsic的首字母,表示这个区域的掺杂浓度很低。
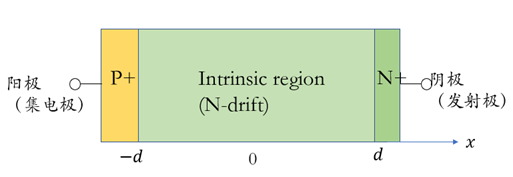
如上图所示,阳极对应IGBT中的集电极,阴极对应IGBT中的发射极。当阴极施加正电压时,PIN处于关断状态,根据前面的分析,阻断状态下主要由掺杂浓度更低I区域承受电压,不再赘述。重点关注阳极施加正电压,PIN处于开通状态的内部载流子工作情况。
在前面,我们讨论了半导体内部的存在固有的复合率,且随着载流子浓度的增加而增加。当PIN结构处于开启状态时,空穴从阳极、电子从阴极注入,所以器件内部的载流子浓度相应增高,从而载流子复合率也会上升。当器件处于稳态时,载流子的注入与载流子的复合应处于平衡状态。
假设处于稳态时的电流密度为 (电流回路中处处相同),空穴浓度分布
(电流回路中处处相同),空穴浓度分布 ,电子浓度分布为
,电子浓度分布为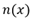 。根据电中性原则,
。根据电中性原则,  。由此,只需要推导出任意一种载流子浓度分布即可。下面以电子浓度为例做简要推导。
。由此,只需要推导出任意一种载流子浓度分布即可。下面以电子浓度为例做简要推导。
稳态状况下的载流子浓度不随时间变化,即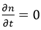 ,所以连续性方程可表达为:
,所以连续性方程可表达为:
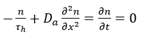
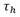 大注入下的载流子寿命。上式左边第一项为复合电流,第二项为扩散电流, 具体可参见第一章的微观电流,并利用了电中性条件下电场
大注入下的载流子寿命。上式左边第一项为复合电流,第二项为扩散电流, 具体可参见第一章的微观电流,并利用了电中性条件下电场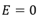 。
。
需要注意的是,这里所采用的扩散系数 不同于自由电子的扩散系数
不同于自由电子的扩散系数 ,
,  被称为双极型扩散系数,其物理解释如下:
被称为双极型扩散系数,其物理解释如下:
半导体中电子和空穴总是成对产生,但是由于其质量的不同,导致其迁移率不同(电子迁移率约为空穴的三倍),从而在相同电场或者相同浓度梯度下,电子比空穴的运动速度更快,导致电子空穴对很快产生空间距离,根据异性电荷相吸的原理,空穴会受到一个与运动速度方向相同的库仑力,加快其运动速度,相反,电子会受到一个与运动速度方向相反的库仑力,降低其运动速度。整体表现为,电子的迁移率和扩散系数减小,而空穴的迁移率和扩散系数增大。

所以,在双极型器件工作过程中,电子的迁移率会降低,而空穴的迁移率会升高,新定义双极性迁移率和双极性扩散系数来表征这个综合效应,表达式如下(推导略),

由此,在稳态状况下,双极性器件的载流子迁移率为0,即没有漂移运动,其运动完全来自于扩散运动。
需要注意的是,上述表征是电子和空穴的综合效应,单独的电子和空穴是存在漂移运动的, 即电子和空穴的漂移运动相互抵消 。
回到扩散方程,其在一维空间的表达式为:

令,  ,上述二阶微分方程的特征解为,
,上述二阶微分方程的特征解为,

系数A和B的求解可借助阳极和阴极边界条件,显然,阴极界面 的空穴电流为0,而阳极界面
的空穴电流为0,而阳极界面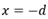 的电子电流为0。
的电子电流为0。
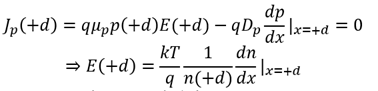
上式推导利用了 ,以及爱因斯坦关系式
,以及爱因斯坦关系式
将电场强度表达式代入 的电子电流表达式,即可得到电流与电荷浓度的关系,即为
的电子电流表达式,即可得到电流与电荷浓度的关系,即为 的边界条件,
的边界条件,
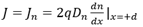
同理,在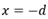 的边界条件,
的边界条件,

利用这两个边界条件,同时利用电中性条件, ,并近似认为电子的迁移率是空穴迁移率的3倍,可以得到载流子浓度与电流的关系如下(详细推导过程略去),
,并近似认为电子的迁移率是空穴迁移率的3倍,可以得到载流子浓度与电流的关系如下(详细推导过程略去),
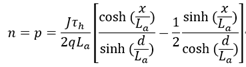

显然载流子在I区的浓度分布是非对称的,因为电子迁移率更大的缘故,载流子浓度最低值靠近阴极。
文末总结
1.稳态状况下的载流子浓度不随时间变化,可表达:
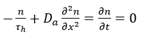
2.半导体中电子和空穴总是成对产生,但是由于其质量的不同,导致其迁移率不同。
3.利用了 ,以及爱因斯坦关系式,可得到电流与电荷浓度的关系,在
,以及爱因斯坦关系式,可得到电流与电荷浓度的关系,在 的边界条件:
的边界条件:
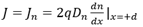
在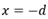 的边界条件:
的边界条件:

4.得到载流子浓度与电流的关系如下:
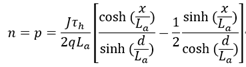
-
IGBT的物理结构模型—PIN&MOS模型(3)2023-12-01 1804
-
IGBT的物理结构模型—PIN&MOS模型(1)2023-11-30 3679
-
IGBT中的PIN结构分析(2)2023-11-28 1490
-
电机驱动器MCU拆解之IGBT分析2023-03-23 2148
-
IGBT的内部结构及特点2021-11-16 4225
-
IGBT模块瞬态热特性退化分析2020-12-10 2065
-
IGBT的基本结构和工作原理等资料合集说明2020-09-10 2895
-
IGBT在固态电源中是如何保护电路的?且看IGBT损坏机理分析2019-12-25 6720
-
简述IGBT模块的内部结构与电路图分析2019-03-05 7385
-
请教分析这个IGBT有没有烧坏2016-01-09 3558
-
IGBT并联技术分析2015-03-11 5766
-
求IGBT失效机理分析2012-12-19 3373
-
IGBT的基础知识--IGBT的基本结构,参数选择,使用注意2010-05-27 13549
全部0条评论

快来发表一下你的评论吧 !

