

零极点的物理本质是什么?如何对系统产生影响?
电子说
描述
每次想弄清楚零极点的物理本质是什么,如何对系统产生影响(大学信号与系统没好好学),网上找一下相关内容,总能看到 ”Hs=A0/(s+a) 极点为s=-a s=jw 所以w=a时增益-20db/十倍频 “类似的结论。
虽然也可以分析电路,但仔细想一想总让人一脸懵逼。s不是等于σ+jw吗,怎么变成了jw,jw又变成了w,而且w=-a又变成了w=a。每次都想把信号与系统重新学一遍(只能怪自己大学摸鱼去了),但看着厚厚的上下册,拖了又拖...... 最近刚好空一点,整理了一些相关内容。
傅里叶变换和拉普拉斯变换:
傅里叶变换 :将时域函数转换为不同频率的正弦波的叠加。
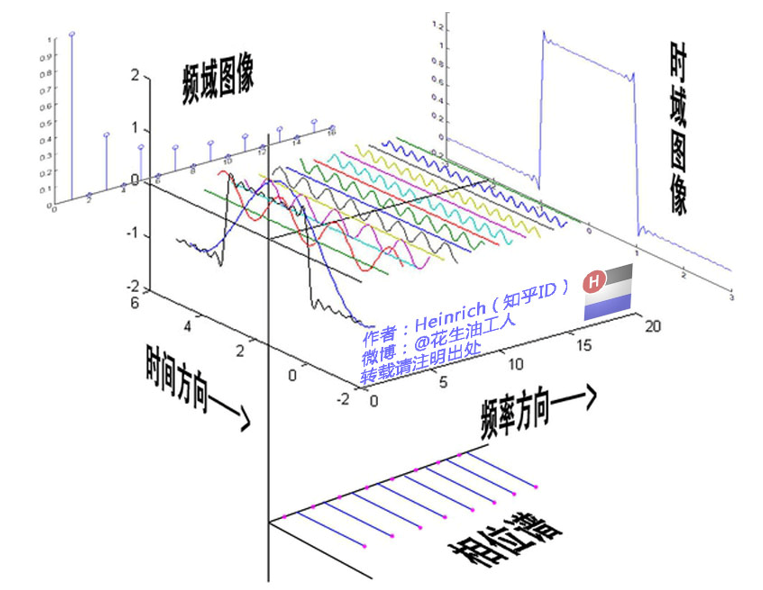
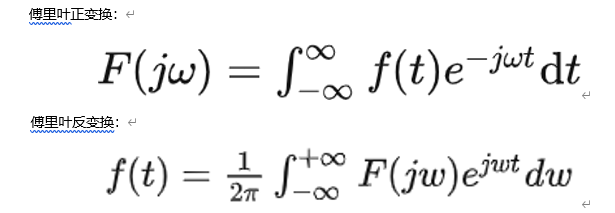
拉普拉斯变换 :
由于傅里叶变换的局限性,要保证f(t)收敛,因此对于非收敛的函数,添加一个衰减因子e ^-σt^ ,使函数在t→∞时,f(t)→0。然后再进行傅里叶变换。


极点的意义:
H(s)=H0/(s-a) 极点s=a 对应的时域原函数:Ht=H0*e^at
由上述分析可知,Hs是Ht×衰减因子做傅里叶变换得到,Gt=H0e^ate^-σt=H0*e^-(σ-a)t 要使Gt收敛,则必须σ>a。
因此可知道极点s=a,是σ+jw=a ,并非jw=a。即σ=a。
极点代表的时域函数可进行拉式变换的收敛域,σ需在极点的右方(见下图,execl做的简易示图,勿喷):
(对于虚数极点s=a+bj,代表σ=a,w=b,a反应衰减速率,b反应震荡频率,虚数极点后续有时间再具体分析)
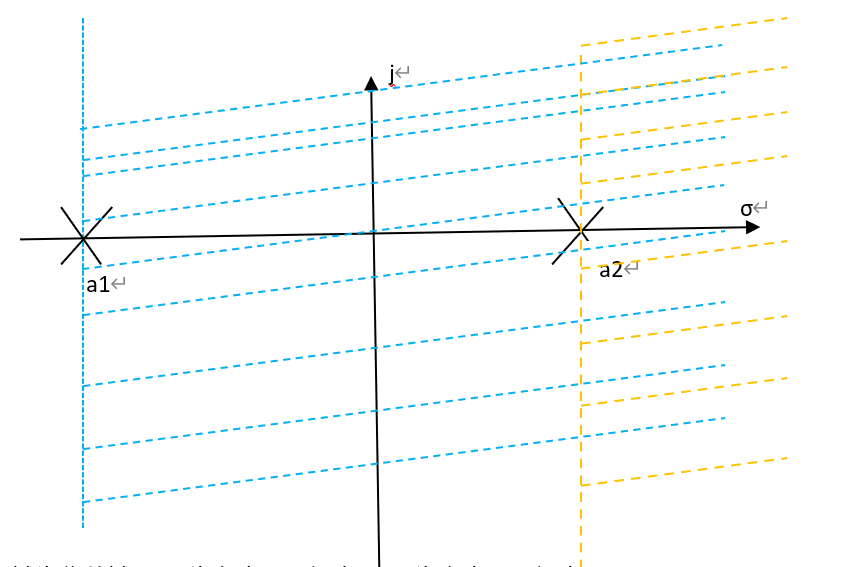
图中阴影部分为收敛域,a1为左半平面极点,收敛域在a1右侧,a2为右边平面极点,收敛域同样在右侧。
由此可由极点位置判断系统稳定性:
左半平面极点:收敛域经过原点,说明σ=0时,时域函数f(t)** e^-σt *收敛,即f(t)收敛。
右半平面极点:收敛域大于零,说明f(t)** e^-σt *中σ必须大于0才收敛,即f(t)不收敛。
另一个问题,为什么s=σ+jw 又有s=jw。其实也就是s域函数与电路的频率响应的转换。
根据拉式变换的微分性质可知道电容的s域参数=1/sc
交流时电容容抗Zc=1/jwc
因此s=jw 只是分别在s域和频域里数学形式上相同,电感同理。
因此知道传输函数Hs,令s=jw可得到电路的频率响应H(w) (此Hw并不是傅里叶变换的Hw)
有了频响函数,电路的幅频特性,相频特性都能很简单的计算出来。
-
零极点仿真分析简介2025-05-28 1020
-
零极点怎么判断滤波器类型2024-08-21 6184
-
什么是零极点电路 零极点仿真原理2024-03-07 4159
-
模拟技术入门之零极点分析(1)2023-11-29 2602
-
零点和极点的作用 复变函数的极点和零点有什么区别和联系?2023-11-08 11360
-
关于dcdc的零点和极点的理解是什么2023-07-28 8598
-
深度解析电路中极点与零点的产生及影响2022-02-22 7922
-
一文搞懂电路的极点和零点2022-02-17 30378
-
这样的零极点系统有什么特点呢?2019-05-20 3295
-
请问什么是零极点?2019-03-13 6255
-
零点和极点的区别及其物理意义2018-03-19 95522
-
电路中极点与零点的产生与影响2016-10-10 1577
-
请问这个电源系统的bode图如何配置零极点?2015-04-07 6161
全部0条评论

快来发表一下你的评论吧 !

