浅析IGBT中的MOS结构—Rds(on)

在推导MOS的IV特性时，我们通过建立了电阻R和电压V之间的关系，从而消除欧姆定律中的电阻R，得到电流与电压之间的关系，但这里所讨论的电阻仅仅是沟道电阻。

对于IGBT中的MOS结构而言，其电阻不仅包括沟道电阻，还包括N-base区域的体电阻。

回顾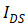表达式如下，

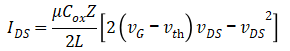
MOS正常工作状态下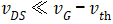， ，可以忽略上式右边第二项，于是沟道部分的电阻可表达为，

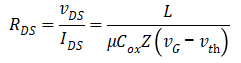
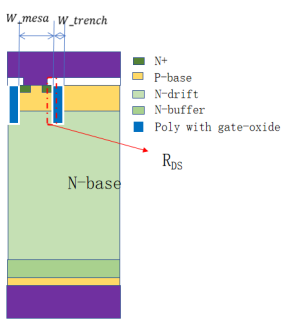
假设如图所示，沟槽之间的MESA宽度为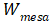，沟槽的宽度为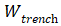，那么对于周期性排布的MOS结构来说，其方阻（电阻乘以面积，即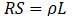）为：

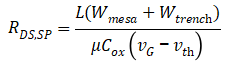
对于N-base区域的体电阻计算，可以做一个简化的推导，简化条件为：

1.电子从MOS沟道注入后，积累在沟槽栅氧的外侧；

2.电子到达沟槽底部后再向下扩散；

3.电子在N-base区域以45°角向背面扩散；

4.扩散路径中各处电子浓度、迁移率相同，即N-base中具有相同的电阻率。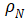

这里对这几个简化条件的合理性做一个说明：

1.因为MOS工作过程中，栅极持续施加正电压，因此靠近栅氧的半导体能带被电子占有的概率更高，所以从源极注入的电子更倾向于在栅氧表面积累；

2.沟道底部距离沟槽底部之间的区域相较整个N-base区域而言，电阻占比很小，计算中可以忽略；

3.稳态工作下，器件内部处于电中性状态，因此内部电场基本可以忽略，电流由扩散电流主导；

4.扩散运动的绝大部分电子分布在45°角的范围内。

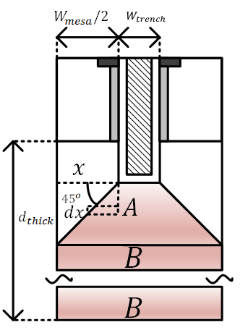
根据电阻的表达式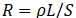：，其中L为电路路径方向的长度，S为电流路径的截面积。显然，可以将体电阻划分为A和B两个区域，A区域为一个等腰梯形，B区域为一个长方形。

A区域的电阻对梯形积分即可计算得到，

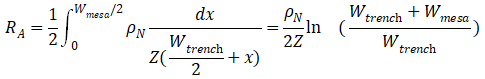
B区域的电阻即长方形的面积，

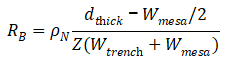
所以，N-base总电阻即将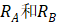相加而得，

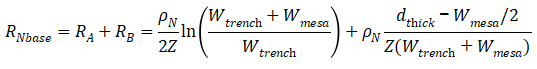
与沟道电阻的方阻计算相似，将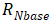乘以面积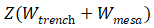即可得到N-base的方阻，并将乘积整理成，

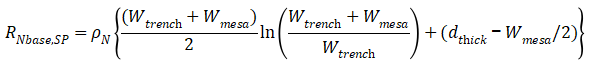
将沟道电阻与N-base电阻相加，即得到MOS的总电阻Rds(on)方阻，

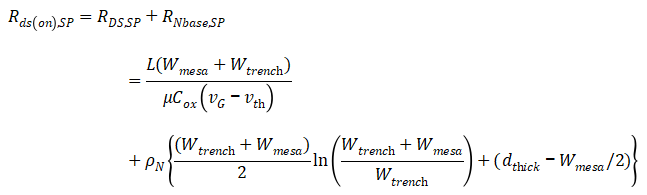
至此，我们就基本完成了对IGBT中MOS结构的静态工作机理分析。

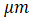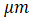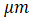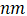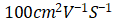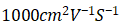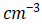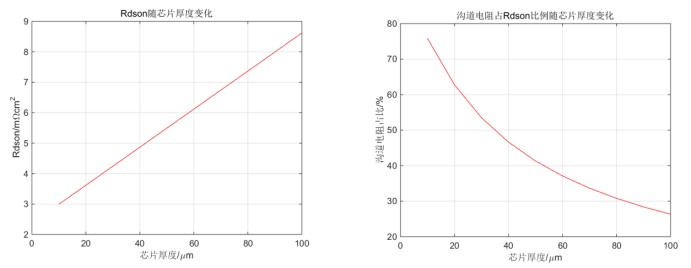
举例，对于一个MOS，其相关参数设计如下，mesa宽度为4，沟槽宽度为1.5沟槽深度为3，栅氧厚度为100，沟道内的电子迁移率，N-base内的电子迁移率，假设在栅极施加电压为10V的条件下，其N-base内的电子浓度为1e16 计算芯片厚度从10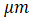增加到100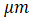，沟道电阻在整体电阻中的占比。