温度传感器(NTC)ADC转换实验

实验环境

Matlab版本： 2021b

操作系统 ：Win10专业版

硬件平台 ：YF-STM32-ALPHA 1R4

实验内容 ：读取温度传感器电压值并转换成实际℃温度显示出来

模型与原理图

本次实验所用到的simulink模型如图5.1所示，电路原图如图5.2所示，其中温度传感器在开发板中的位置如图5.3所示，实验效果为读取NTC温度传感器所在引脚PA4的电压值，然后通过查表算法将其转换成实际℃温度值并通过仪表或“display”模型控件显示出来。

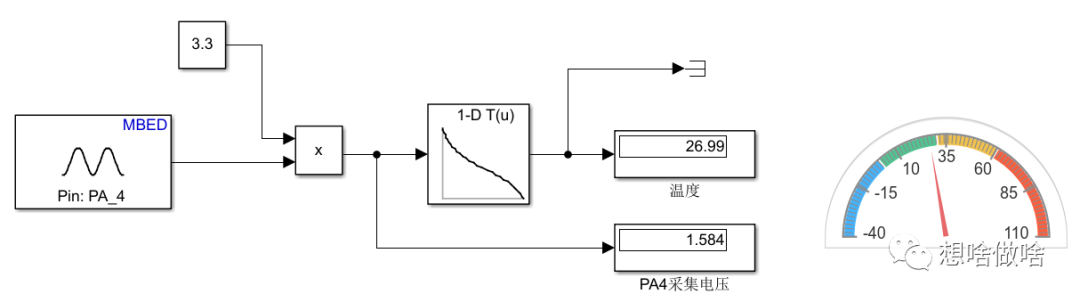
图5.1 NTC温度传感器采集simulink模型

图5.2 温度传感器电路图

图5.3 温度传感器在电路板中位置

基础模型介绍与分析

本次实验所用到的NTC(负温度系数)传感器外观如图5.4所示，因其低廉的价格和使用方便的特性，被广泛应用于家庭与工业电子设备中(空调、电饭锅、洗衣机等)。表5.1为该温度传感器基本使用参数，详细的温度电阻特性参考其特性表链接，里面详细整理了该传感器电阻值与温度的对应关系。电压采集原理图采用“分压式”接法，如图5.5所示，单片机端采集电压公式计算方法 MCU_ADC = Rt*3.3V/(10+Rt)。

图5.4 温度传感器外观

表5.1 基本参数表

型号	B值	使用温度范围
MF52-103/3435 10K ±1％	3435 1%	-55℃~125℃

温度阻值特性表：https://pan.baidu.com/s/1dF19CoL? at =1700414024610

图5.5 NTC温度传感器“分压”测电压接法

Analog Input”模型外观如图5.6所示，通过更改“Pin”栏参数可以读取该引脚的电压值，读取的数值范围为0~1，需要注意的是“Pin”栏参数只有该芯片引脚支持模拟量功能才能使用

图5.6 "Analog Input"模型

为方便读者以往单片机使用习惯和计算方便性，实验中使用到乘法模型“Product”将读取的ADC值乘以3.3倍放大处理，得到的最终值范围为0~3.3，如图5.7所示。

图5.7 "Product"模型使用方法

查表法转换温度值

这是本次实验中的关键算法部分，也是在嵌入式开发中针对A/D方式读取原始传感器数据参数常用的转换方法，即大家熟知的“以空间换时间“法，“ Lookup with Linear Lagrange Interpolation ”模型与参数设置窗口如图5.8所示。

图5.8 " Lookup with Linear Lagrange Interpolation"模型

我们首先通过“温度阻值特性表”得到温度电压表关系，考虑到在单片机中不占用太大存储空间，这里采取每5℃间隔制作表格，一般对于精度要求不是特别高的场合，我们可以大致认为5℃内的温度变化是线性的，其中“V”的电压值计算公式为V = R*3.3V/(10+R)，将其中的R值代入，就可以得到V的最终值，详情请参考表5.2。

NTC_Value_table.xlsx

表 5.2 温度-阻值-分压表

T	R	V
-40	190.5562	3.135457592
-35	151.5975	3.09578892
-30	116.3519	3.038824663
-25	90.0326	2.970107545
-20	70.5811	2.890474689
-15	55.7284	2.797933922
-10	44.1201	2.690245029
-5	35.0362	2.567256118
0	28.0170	2.431967278
5	22.6597	2.289580431
10	18.5600	2.144537815
15	16.2797	2.044277903
20	12.6900	1.845614808
25	10.0000	1.65
30	8.1600	1.482819383
35	6.8133	1.337268115
40	5.7340	1.202631244
45	4.8286	1.074570762
50	4.065	0.953750444
55	3.4146	0.839993738
60	2.825	0.726900585
65	2.5076	0.661604145
70	2.135	0.580593325
75	1.8225	0.508712201
80	1.586	0.451734852
85	1.4006	0.405415504
90	1.236	0.363011748
95	1.0744	0.320154591
100	0.918	0.277468401
105	0.787	0.240762028
110	0.713	0.219630356

点击“Lookup with Linear Lagrange Interpolation”模型参数设置窗口中的“编辑表和断点...”如图5.9所示，弹出的查找表参数设置如图5.10所示，将表5.2中的温度T和电压值V填入该表中的“表数据”和“断点 1”处，注意数据的升降序和填写位置

图5.9 表格参数设置按钮

图5.10 查找表参数填好效果

点击“线性图”按钮查看填写的数据对应的曲线是否正确，如图5.11所示，最终填写好的数据效果如图5.12所示。

图5.11 点击查看线性图曲线

图5.12 填写好查找表数据的模型参数设置部分效果

总结

本次实验以一个基本的温度传感器为例，通过在其中加入查表算法将其转换成我们熟知的摄氏度(℃)温度值，但是在实际场景中经常会出现一些杂波电压或采集的数据与我们所需要的数据稳定的情况，读者朋友可以思考下面对这种问题该如何去解决？以往使用C代码方式一般是在前面加入杂波滤除算法然后再求平均值，simulink中又该如何使用呢？

拓展延申

1、本次实验又用到一个数据显示仪表，但是文章中并没有做过多介绍，其位于“Dashboard”库中，里面又很多显示仪表和按钮开关，在实际模型测试中非常方便，读者朋友可以多去尝试使用。

图5.13 “Dashboard”库位置

2、在查表法建立表格过程中，有一个操作非常繁琐，复制到表格中的数据非常不方便，如果有多种传感器需要建立表格，那工作量是不可想象的，其实这里有个更方便的方法，可以先建立一个excel表格，然后使用matlab打开并导入到matlab中，如图5.14和图5.15所示，然后在matlab中直接定义两个数组变量，然后在“表数据”和“断点1”中引入即可，如图5.16所示，至于该方式更深入的用法，大家可以积极去探索下，这里暂时不做过多介绍。

图5.14 打开Excel表格

图5.15 将Excel表格的数据导入为变量表

图5.16 通过变量数组引入查找表