

抖动的基础知识
描述
一、背景
抖动的定义是“信号的各个有效瞬时对其当时的理想位置的短期性偏离。”简单来说,抖动是指相对于其应当发生跳变的时间,信号实际跳变时有多长时间的提前或延迟。对于数字信号而言,这个有效瞬时就是信号的 跳变点 (或交叉点)。这取决于时间参考是来自于采样数据,还是由外部提供。如果抖动发生在采样点跳变阈值的“错误位置”,并且导致接收电路“错解”了该比特位发射时的真实情况,那么就会出现传输误差。图 1 就是对这种情形的描述。
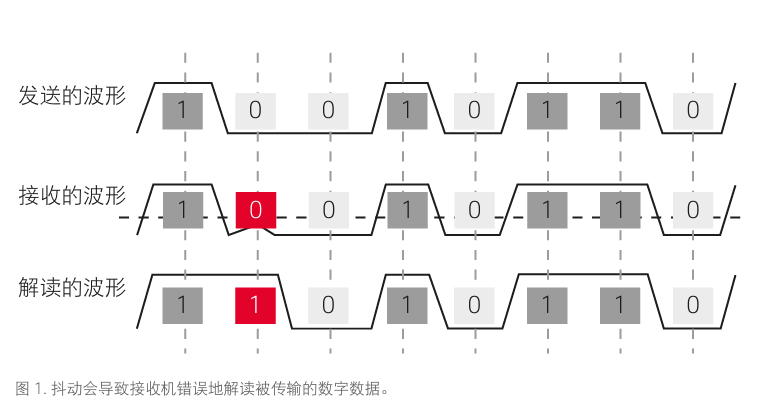
注:对抖动的深刻理解,有助于我们设计类似时钟、serdes、PLL、RF等对抖动指标敏感的电路。
二、抖动源
信号上的抖动会因各种原因而呈现出不同的特点。因此,对抖动源进行分类至关重要。下面列出了容易引起抖动的主要情形:
1、系统情况
这是数字系统本身在模拟环境下的特性对信号造成的影响。与系统相关的抖动源包括:
①辐射信号或传导信号之间的串扰
②散射效应
③阻抗失配
2、数据相关现象
传输数据的码型或其他特性会对到达接收机位置的净抖动(net jitter)造成影响。与数据相关的抖动源包括:
①码间干扰
②占空比失真
③伪随机、比特序列周期性
3、随机噪声现象
这里指的是,系统中随机引入的噪声会导致抖动现象的发生。此类抖动源包括:
①热噪声 — 即 kTB 噪声。它与导体中的电子流紧密相关,并且会随着带宽、温度和噪声电阻的增加而增加。
②散粒噪声 — 半导体中的电子噪声和孔噪声(hole noise),此类噪声的幅度取决于偏置电流和测量带宽。
③“粉红”噪声 — 频谱与 1/f 相关的噪声
上述现象在所有的半导体和元器件中都会发生,因此在锁相环设计、振荡器的拓扑结构和设计及晶体材料性能测试时都会遇到。
4、有界和无界抖动抖动
源通常分为两类:“有界”和“无界”。
有界抖动源会在可识别的时间间隔内达到最大和最小的相位偏差值。这类抖动也叫“确定性抖动”;它们是由系统和与数据相关的(前述的第一组和第二组)抖动源而引发的。
无界抖动源在任何时间间隔内都不会出现最大或最小的相位偏差,而且至少理论上,它们的抖动幅度会趋于无穷大。这类抖动也会被归类为“随机抖动”。它们会因为随机噪声源(上述第三组抖动源)而引发。
信号的总体抖动可以用相位误差函数 φj (t) 来表示。它是“确定性抖动分量”和“随机抖动分量”的总和,这二者都会影响信号质量:
φj (t) = φj (t)D + φj (t)R
其中 φj (t)D 代表“确定性抖动分量”,采用峰峰值(Jpp D)进行量化。它通过把确定性/有界抖动源产生的相位(或时间)上的最大提前量和最大延迟量相加而得到。
φj (t)R 代表“随机抖动分量”,采用标准偏差值(Jrms R)进行量化。它是所有会影响信号质量的随机噪声源的总和。由于我们是假设随机抖动呈现高斯分布,并用高斯分布的平均值和标准方差来定义随机抖动。若要确定随机噪声源产生的抖动,必须确定和评估代表这种随机抖动的高斯函数和它的标准方差。
5、抖动眼图
眼图对抖动进行了最基本、最直观的视图显示。它是把捕获到的波形当中的所有比特周期相互叠加之后,所得到的复合视图。换言之,就是把周期 2 到周期 3 的波形轨迹叠加在周期 1 到周期 2 的轨迹之上;并且以此类推,对所有的比特周期进行叠加。
图 2 是一个理想的眼图,交叉点左右两边的跳变都非常平滑、对称。中间大大张开的“眼睛”就是对每个比特位进行采样的理想位置(“x”标记处)。如果把采样波形的高值或低值设置在这个采样点上,就会使出现比特误码的可能性降到最低。
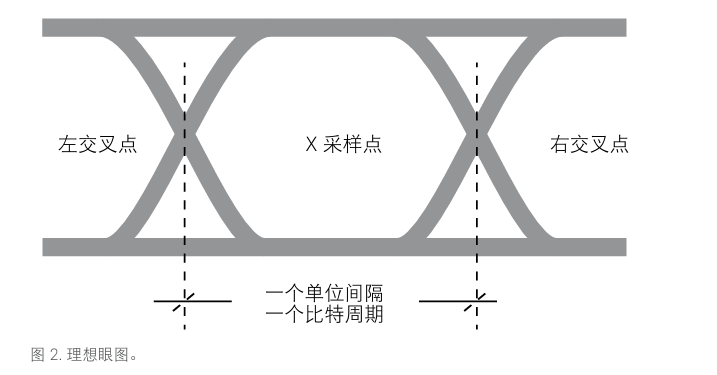
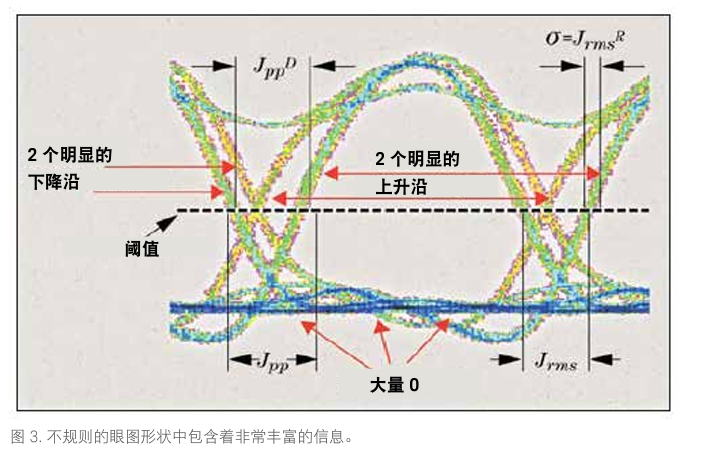
图 3 是一个非理想波形的眼图。但是,这种不规则的形状却给我们带来了大量信息 — 而且不需要进行更复杂的测量。我们可以看到:底部的幅度变化比顶部小,信号携带的 0 的数量明显多于 1 的数量。底部有四条轨迹,因此在一行当中可能会至少出现四个 0。而顶部的轨迹只有两条,因而这个波形在一行当中最多只有两个 1。波形中有两个不同的上升沿和下降沿,这说明其中存在确定性抖动。上升沿的展宽比下降沿大,而且一些交叉点相交于阈值电平以下,这意味着存在占空比失真,而且 0 比特的周期或驻留时间比 1 长。
三、抖动的其它查看方式
简要介绍过抖动之后,我们再了解一些其他测量和查看抖动的方式。抖动会对系统或器件造成不良影响;每种测量方式对于深入了解抖动属性,都有其各自的优势。如能站在全局高度对这些要点加以“整合”,我们就可以透彻地了解抖动,轻松找到抖动根源,并且灵活地选择减少或消除抖动的方式。
1、直方图
直方图是对数值数据分布情况的图形表示;这里选定的参数通常是时间或幅度(在 X 轴上显示)和发生频率(在 Y 轴上显示)。直方图拥有比眼图更深一层的洞见力,它对于了解电路和执行故障诊断非常有用。此外,在数字总线标准中所要求的抖动分离例程中,直方图(尤其是 TIE 直方图)都是必不可少的基本数据集。
在进行故障诊断时,上升时间、下降时间、周期和占空比等波形参数,均可用直方图表示。这些直方图可以清楚地显示出多模性能分布等条件。然后,这些条件可被用来与传输模式等电路条件相关联。
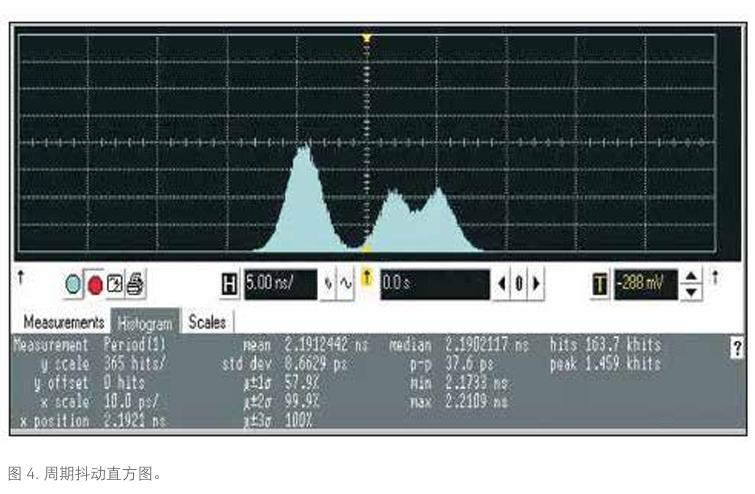
图 4 是一个周期抖动的直方图。左侧驼峰呈现正常的高斯形状,但右侧有两个波峰。进一步分析之后我们发现:这个时钟参考信号的二次谐波和四次谐波是造成抖动的根源。针对一次波形捕获,它可以显示出 TIE 值在所有比特跳变中出现的频率。这是直方图的一个最重要的应用。
2、浴缸曲线
“浴缸曲线”提供了另一种查看抖动的视角,如图 5 所示。“浴缸曲线”的得名是因为其特征曲线看起来很像一个浴缸的横截面。浴缸曲线是 BER 值在完整的单位间隔内,随着采样点的变化而形成的曲线图。(请参见附录提示,以便进一步了解关于单位间隔的详情。)它描述了采样时间与 BER 值之间的函数关系,通常以对数标度进行显示。
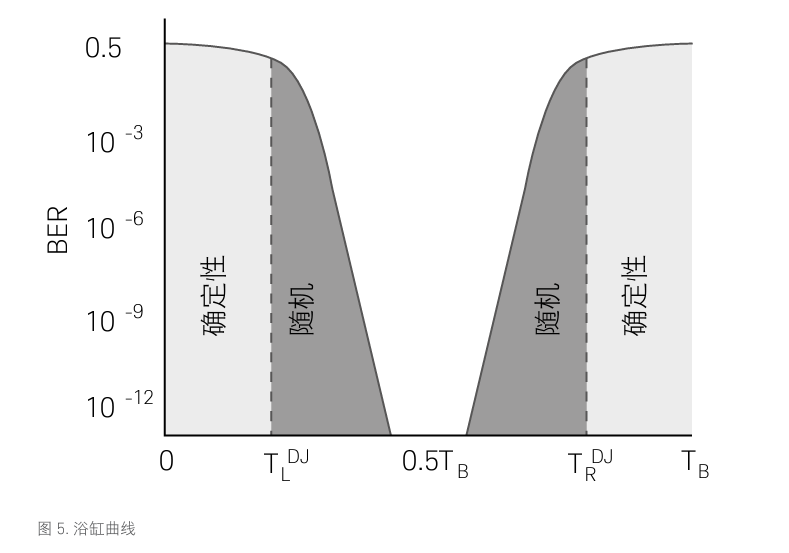
当采样点位于或靠近跳变点时,BER 为 0.5 — 比特跳变的成败概率各占一半。这些区域内的曲线相当平坦,绝大部分是确定性抖动。在一个间隔内,当采样点从两端向内移动时,BER 出现了陡然下降。这些区域以随机抖动现象为主,且 BER 的大小取决于产生随机抖动的高斯过程的标准方差。正如所料,这个间隔的中心位置恰好是最佳采样点。
请注意,有采样周期的中间时间上进行了一次 BER 测量。同样地,通过“眼球”外推法,我们可以估算出这条曲线在单位间隔的中间位置上,BER 值将会超过 10–18。如此一来,即使是 10 Gb/s 的系统,若想得到这个值,也会需要超过 3×108 秒的时间。
浴缸曲线可以直观地显示出预期的 BER 级别的传输误差裕量。在指定了 BER 值(通常为 10-12)的条件下,左右边沿的距离越远,抖动容限就越大。当然,两个边沿之间的距离越近,则容限就会越小。这些边沿与从 TIE 直方图导出的高斯函数的尾部直接相关。浴缸曲线还可用于分离随机抖动和确定性抖动,以及确定随机分量的标准方差。
3、频域抖动的优势
另一种分析抖动来源的方法是在频域中进行查看。确定性抖动源在频域中显示为线性谱图。这种频域视图可以借助相位噪声或抖动频谱分析来生成。所以,它会涉及到相位噪声以及相对于载波或时钟而言,抖动随频率发生的偏移变化。相位噪声测量,由于可在测量过程中进行有效的过采样和带宽控制,因此可以帮助实现最精确的抖动评估。这种测量对于检测设计问题,特别是查找锁相环或晶体振荡器的设计缺陷,可以说是“独具慧眼”。它可轻松识别杂散信号引起的确定性抖动。这类测量有助于优化时钟恢复电路,和发现杂散与噪声的内部成因。
相位噪声测量也可以集成到特定带宽内,生成完全整合的抖动信息;尽管它无法直接转化为数据通信标准所指定的峰峰值抖动。
图 6 是一个锁相环的固有抖动线性谱图。噪声峰值出现在 2 kHz 偏移处。图中还有用于识别确定性抖动源的频率线。这些从 60 Hz 到接近 800 Hz 的线是电源线杂散。2 到 7 MHz 范围内明显的频率线最可能是由时钟参考引起的杂散,它们产生了确定性抖动。
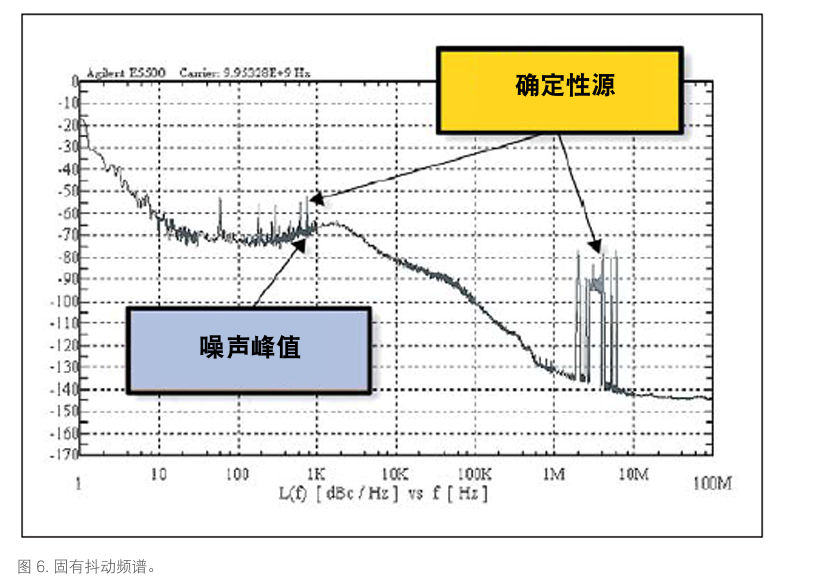
对 TIE 数据进行快速傅里叶变换(FFT) 是了解频域抖动的另一种途径。FFT 的分辨率要比低电平相位噪声视图低很多,但是这种极为简单快捷的方法非常适合查看高电平现象。
四、结论
在开发产品时,处理抖动是非常重要的一个环节。有界抖动(即“确定性抖动”)通常是由系统本身或与数据相关的现象导致。无界抖动是由随机噪声而引发。为了分析这些抖动类型的影响,可以综合借助眼图、直方图、浴缸曲线,以及时域频率等抖动测量方法,充分发挥它们各自的优势,让问题迎刃而解。这些信息可以帮助工程师们找出抖动根源,选择最佳途径减少或消除抖动,从而提高其设计对象的传输性能。
-
QC基础知识2010-06-02 1470
-
labview基础知识2018-03-08 6451
-
高电平的抖动问题2018-09-17 2684
-
通信基础知识教程2010-03-04 917
-
软板基础知识2006-06-30 1504
-
电子电路基础知识2008-01-15 247728
-
电池基础知识(集全版)2009-11-10 2902
-
电池隔膜基础知识2009-11-17 1515
-
计算机基础知识介绍2015-12-03 994
-
使用Eclipse基础知识2016-02-26 953
-
synplify基础知识说明2016-06-17 2261
-
电源管理基础知识电源管理基础知识电源管理基础知识2017-09-15 1689
-
时钟抖动解秘—高速链路时钟抖动规范基础知识2022-11-07 686
-
抖动与抖动测试的基础知识2023-02-10 3406
-
优质LDO基础知识分享2023-03-26 2091
全部0条评论

快来发表一下你的评论吧 !

