如何通过Matlab进行零极点求解？

　　本文主要尝试回答以下三个问题：

　　（1）系数已知的传递函数怎么求其零极点？

　　（2）系数为变量的传递函数怎么求其零极点表达式？

　　（3）只知道一组节点方程，如何推导系统传递函数？

　　01

　　系数已知的传递函数怎么求其零极点？

　　1.1 问题

　　如果我们拿到了一个传递函数，其所有系数是已知的，怎么计算其零极点？

　　1.2 解决方法

　　Matlab可通过两种模型描述系统的传递函数，这两种模型是：传递函数模型、零极点模型。它们之间是可以互相转化的。如果一个系统传递函数的所有系数已知的，我们只要将其描述成传递函数模型，接着将其转换成零极点模型。一旦完成转换，我们就可以观察到系统的零极点大小。此外，我们还可以画出传递函数的零极点图，更加直观的看到零极点的分布位置。

　　EG1：如果a=1，求解G=（2*s+1）/（a*s^2+2*a*s+1）的零极点，Matlab代码如下：

　　

　　图↑ 代码

　　

　　图↑ 转换为了零极点模型

　　

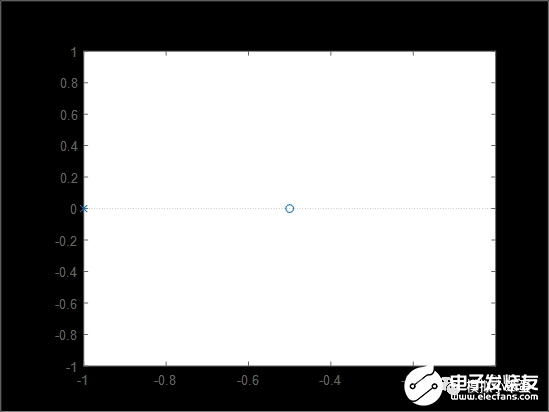
　　图↑ 零极点MAP图

　　1.3 写在最后

　　Matlab默认的传递函数模型一定是拉普拉斯形式的，它的输入一般包括直接输入和矩阵输入。如果使用直接输入的方式，需要在输入之前定义Laplace算子，只有这样Matlab才能视其为传递函数模型。

　　step（ ）、bode（ ）等分析方式只对传递函数模型有效

　　Laplace变换和其反变换只能针对符号表达式进行。也就是说，你对一个时域函数进行Laplace变换后得到的Lalace表达式，虽然在我们看来就是传递函数，但Matlab并不会视其为传递函数模型（除非定义Laplace算子后重新输入一遍Lplace表达式）

　　02

　　系数为变量的传递函数怎么求其零极点表达式？

　　2.1 问题

　　你有没有面临过这样一种情况：当你设计一个OP时，为了计算出它准确的传递函数，你首先画出包含各种寄生电容效应的小信号模型图，然后经过了艰难的计算，终于让你算出了传递函数的表达式。为了稳定性设计，你需要知道它的零极点分布情况。这时候你需要接着对传递函数进行第二次的求解，目的是为了求得零极点表达式。只有这样你才能清楚地知道零极点和哪些参数相关，来指导你在设计上实现优化。

　　但有时候，零极点表达式的计算是很困难。

　　基于上述的问题，尤其是当一个传递函数包含未知参数（多于1个）时，我们有没有可能借助Matlab工具计算出零极点公式呢？回答是：如果传递函数是二阶的，利用Matlab求零极点表达式是容易实现的。但对于更高阶的系统而言，想通过Matlab来求得解析解是极其困难的。

　　我们通常求解传递函数的零极点，其实就是求解传递函数其分子或分母的根，那么该问题本质上就是一个求方程解的问题。该问题或可借助Matlab工具辅助解决。

　　Matlab的符号运算工具箱提供了一个solve（）函数，该函数可以用于一般线性或非线性方程的解析求解，可以用来试着解决我们所关心的问题。

　　2.2 solve（）函数简介

　　solve的调用形式：

　　solve（eq）

　　solve（eq， var）

　　solve（eq1， eq2， …， eqn）

　　solve（eq1， eq2， …， eqn， var1， var2， …， varn）

　　eq为符号表达式，var为指定的要求解的变量。如果不声明要求解的变量（第一和第三种形式），则matlab自动按默认变量进行求解。

　　下面试着以一个通用一元二次方程的求解例子来理解solve（ ）函数。

　　EG2：试对一个典型的一元二次方程y=a*x^2+b*x+c进行求解。Matlab的实现代码和结果如下：

　　

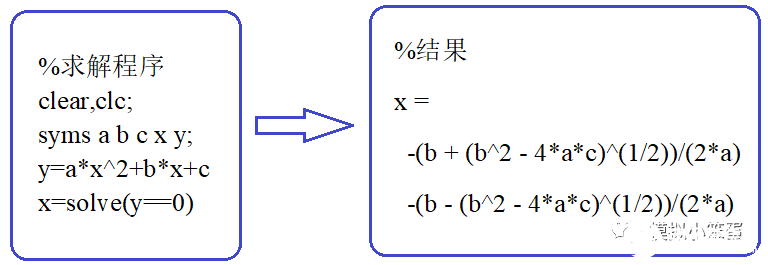
　　图↑ 程序及结果

　　程序计算得到的结果是一元二次方程的通解，对于该结果我们应该是相当熟悉的。

　　2.3实际传递函数根的求解

　　EG3：下图为拉扎维书上一个共源极放大器的例子，给出了该电路的精确传递函数。

　　我们先观察该传递函数，发现它是一个二阶系统。由于所有二阶传递函数的分母的其实都是a*x^2+b*x+c的形式，表达式中的各个电阻、电容可以申明为变量。如此一来，此例的实现和EG2并没有什么不同。令分母等于0，求解的结果便是系统的极点了。此例中零点可以直接观察得出。

　　

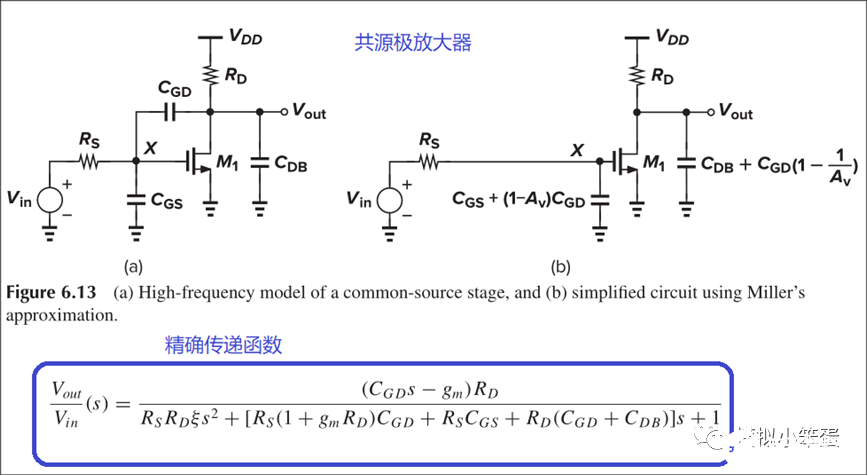
　　图↑ 拉扎维书上的内容

　　思考这样一个问题：我们真的需要借助Matlab对诸如此类的二阶系统求零极点表达式吗？

　　如前所述，我们很清楚一个二阶方程a*x^2+b*x+c=0的通解是什么，那么就可以直接应用该公式进行极点求解，这时候用Matlab就有点多余了。

　　那么对于更高阶的方程，比如三次方程，Matlab能够胜任解析求解吗？答案是不能。因为一个通用的一元三次方程是没有通解的，因此想通过简单申明变量、借助Matlab求其解析解的想法注定难以实现。需要注意的是，虽然三阶方程没有通解，但并不代表其没有解，它的解是根据判别式的不同而不同的。而如果明确知道这个判别式，便可以将其作为一个新的约束方程，和传递函数进行方程联解，这时候是有可能求出结果的。

　　在实际模拟电路的设计中，我们通常会通过“假设-保证假设成立”的方式来简化方程求解。刚才说到的“判别式”像极了我们电路设计时的种种假设条件，所有的计算都有赖于这个前提的成立。关于eg2，在书中拉扎维不就假定主极点远远小于次极点来简化零极点计算的么。倘若这种假设是合理的，这将为快速估算提供新的途径。但是，这种堪称宇宙无敌的假设法，一般人是用不了的，比如我就经常碰到这样的问题：自认为完美的假设，在一圈计算下来之后才发现前提是不成立的。两种假设之间的差别或许就代表着我和大神之间的距离，这多少有点打击自信心。

　　至此可以做个小结：

　　对于包含变量的传递函数，如果其是二阶的，利用Matlab求零极点表达式是容易实现的。但对于更高阶的系统而言，想通过Matlab来求得解析解是极其困难的。

　　Matlab解出的表达式即使是准确的，仍需要我们自己去对公式进行近似。或许近似的公式不绝对准确，但却可以用于指导设计。

　　2.4写在最后

　　对于电路系统：

　　对于一个电路系统，它有可能是单输入、单输出的，也有可能是多输入、多输出的。对于前者，其传递函数是一个一元方程；而对于后者，其传递函数通常是一个方程组。但无论是哪种情况，都可以使用solve（）函数尝试对其求解 。

　　关于Matlab的符号计算：

　　计算精确：符号计算基于数学公式、定理并通过一系列推理、演绎得到方程的解或者数学表达式的值，对操作对象不进行离散化和近似化处理；

　　应用范围有限：实际科研和生产中遇到的问题绝大多数都无法获得精确的符号解，这时我们不得不求助数值计算；

　　对符号计算态度：用其来完成公式推导和解决简单的对计算时效性要求不高的问题，综合符号计算和数值计算各自的优点，视问题特点混合使用符号计算和数值计算。

　　关于solve（）：

　　solve（）函数适用于单变量方程（比如只有x一个未知数 ）或多变量方程（比如本文例子中有a，b，c，x，y多个变量）的求解。但该函数能求解的前提是求解对象确实存在解析解，如果没有，那么只能求解数值解，但数值解需要传递函数的各系数已知。

　　03

　　只知道一组节点方程，如何推导系统传递函数？

　　3.1 问题

　　针对一个小信号模型，如果我们只能根据KCL/KVL列出节点方程，因此可以得到一组节点方程。我们能否借助Matlab工具根据节点方程组推导出传递函数呢？

　　3.2 解决方法

　　

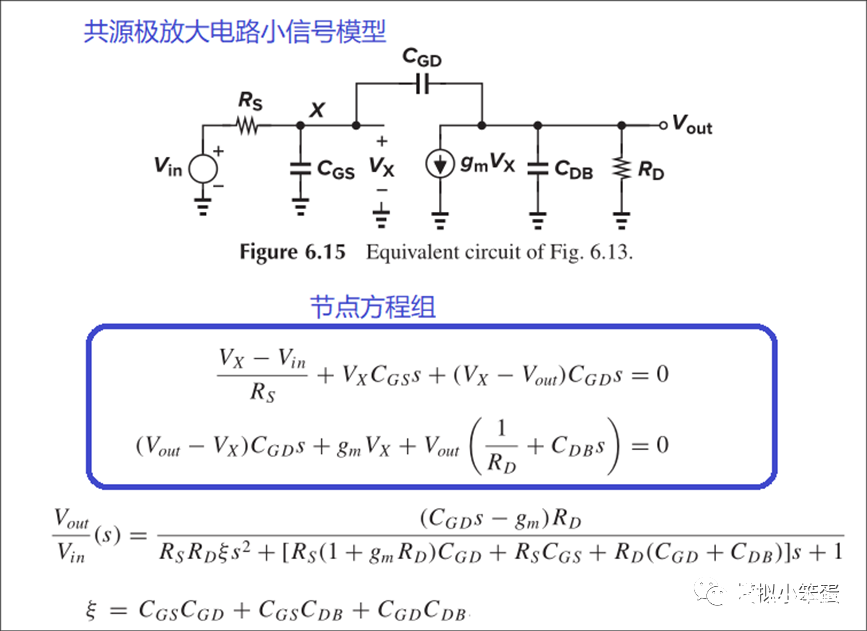
　　图↑ 书上的一个例子

　　如上图，这是拉扎维书上的一个例子，我们试着编写程序，看看能否利用两个节点方程推导出传递函数。

　　程序如下：

　　

　　图↑ 代码

　　运行结果：

　　

　　图↑ 运行结果

　　直接求出的H1结果是正确的，但式中还带有变量Vx，虽然上下式中都有，可以化简掉，但该结果总是不那么理想。因此对H1进行合并同类项后得到H2，可以看到H2完全按照降幂排列，且已经化除了Vx，表达式和书上的完全一样。

　　看来，利用Matlab是可以实现传递函数的推导的！

　　3.3 写在最后

　　其实推导传递函数本身并没有什么难度，即使手算无非也就是多花点时间，Matlab只是能让我们偷个懒而已，况且你是否敢完全相信软件的推导结果呢？

　　更有意义的是如何面对一个传递函数，比如了解它的零极点分布，了解怎样在参数之间取舍才能得到一个稳定的系统。而这，软件似乎无能为力。

审核编辑：黄飞