

模拟IC设计之OP带宽的计算方法
模拟技术
描述
OP单位增益带宽的计算
在实际的建立过程中, 运放由于有限的带宽, 建立速度不可能无限大, 因此就存在建立误差。只有保证运放的闭环带宽足够大, 才能保证 MDAC 的建立精度满足系统要求。
假设运放闭环的时间常数为τ,MDAC 的反馈系数为β 。闭环系统的输出表达式为:
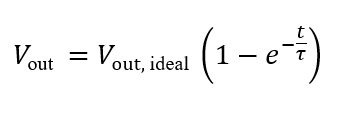
公式(1)
为了便于计算和分析, 可以将放大相的 MDAC 闭环电路近似为单极点系统。线性建立情况下时间常数和运放 GBW 的关系为:
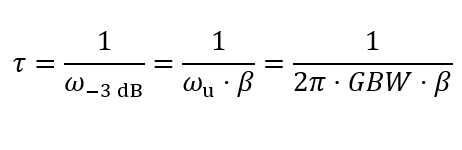
公式(2)
上式中,ω-3dB表示闭环系统的-3dB带宽,ωu表示运放的单位增益带宽。
建立误差为:
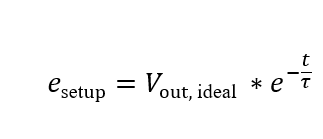
公式(3)
接下来我们将这个误差量折算到ADC的最前端,折算的方法是将该误差除以前向增益。根据前文的ADC架构图,设当前级为第i个流水级(i=1~M),折算到输入端的误差为:
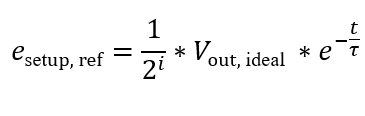
公式(4)
建立误差最大值应该小于系统整体分辨率的1/2。则有:
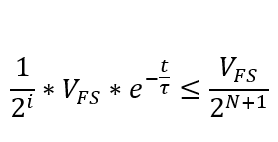
公式(5)
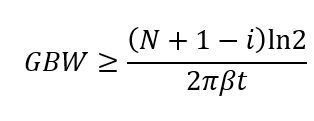
公式(6)
t为分配给MDAC的输出建立时间。若FCLK表示时钟频率,则可用表示分配的建立时间的大小,带入上式:
公式(7)
若α=1/2,则表示MDAC的输出需在时钟一半周期以内完成建立。式(7)表明, 系统采样频率越高, 对运放的带宽要求也越高, 对于多位的 MDAC, β越小, 那么也要求更大的带宽。而更大的带宽,往往意味着更大的功耗,因此高速应用的 ADC 和多位结构的流水线级意味着更高的功耗。
根据公式7,对一个9bitADC尝试计算,计算结果如下表所示:
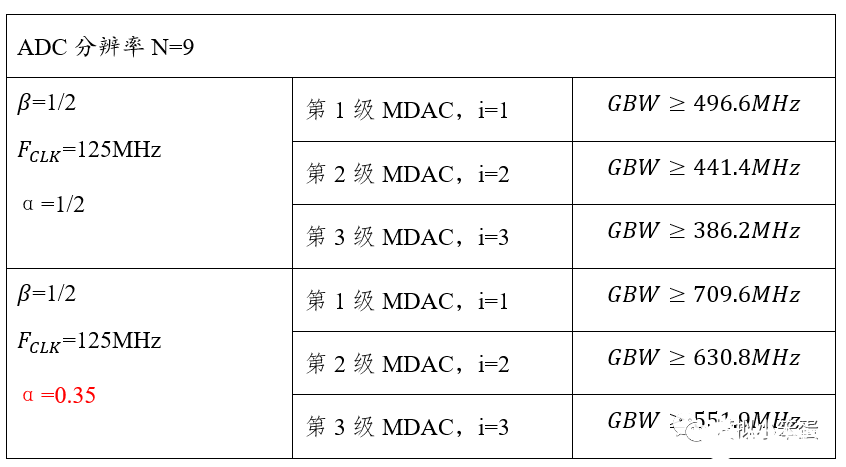
注意:
β值受Cp的影响,实际会小于1/2。α实际中也小于1/2,因此实际GBW要比上表得到的值更大。
公式7也适用于S/H中OP的计算,但要取β=1,i=0。
电路设计中的计算是非常重要的,但在计算之外,还有更高的境界,那就是“经验”的运用,即知道如何留余量,留有多大余量,条件受限的时候怎样“丢车保帅”等,或许这就是模拟电路所谓的“艺术性”真正所在的地方吧。
一个人,学会了所有的理论,懂得了如何去计算,他一定可以设计出鲁棒性很好的电路吗?我想答案是不一定。之所以是“不一定”,是以对这个世界的敬畏心,将小概率预留给真正意义上的天才,我相信有这样的人存在。但对于大多数人而言,理论和实践之间的鸿沟需要拿经验的桥梁才能跨越。
有两个最最朴素的理由,使我相信经验的价值。其一,我们使用的计算模型很多时候是简化模型,与客观世界之间存在误差;其二,系统性问题非单一原理所能解释。这两点都决定了我们设计出的东西一定存在一个边界。而经验的价值在于我们可以通过“留有余量”和“加固设计”的方法来达到扩充边界的目的,使我们设计出的东西具备更强的适应性。
审核编辑:黄飞
-
【SOC的多种计算方法】2024-06-05 5307
-
电荷放大电路的带宽 和IV转换电路带宽计算方法不一样吗?2024-09-03 450
-
阻抗计算方法2013-06-10 3190
-
机器视觉计算方法2015-08-14 7918
-
Rstart的计算方法2021-10-29 2059
-
IFFT的计算方法2008-10-30 14182
-
AGP、PCI-E总线带宽的计算方法2009-05-09 3943
-
互阻放大器带宽计算方法2011-07-11 8640
-
甲类单端的简易计算方法2016-01-19 1084
-
油藏数值模拟有限元并行计算方法研究_张允2017-03-20 1036
-
特征阻抗的计算方法2017-06-09 3030
-
公路坡度的表示和计算方法综述2021-08-11 1120
-
EMC计算方法和EMC仿真(1) 计算方法简介2023-02-14 4434
-
EMC计算方法和EMC仿真(1) ——计算方法简介2023-12-05 2902
-
模拟IC设计之OP的指标计算方法2023-11-30 1873
全部0条评论

快来发表一下你的评论吧 !

