

模拟IC设计之OP的指标计算方法
描述
我们知道,一个处在系统中的组件,总会有一些指标是需要满足的。自然,pipelinedADC中的OP也要满足一定的增益和带宽指标。
PipelinedADC中的OP主要分布在S/H电路和MDAC电路中。单就运放指标计算而言,无论是S/H还是MDAC,都可以作为同一类问题处理——即运放闭环系统的性能问题。运放有限增益导致即使时间足够长,输出仍然存在一个直流误差;运放的有限带宽导致在限定的时间窗口期内,输出并不能实现100%精度的建立。要使误差在系统允许范围内,运放的增益和带宽必须要达到一定限值以上。
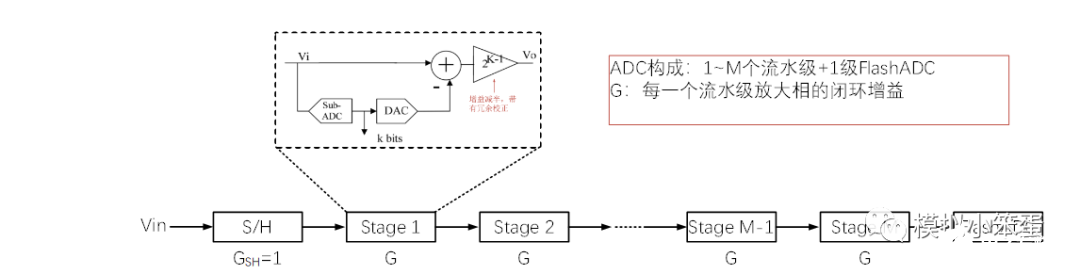
图:ADC架构图
在计算之前,我们有必要先了解一下ADC的架构,这对理解计算过程是有帮助的。我们看上图,它由S/H电路、1~M个流水级和一个FlashADC组成。图中G表示每个流水极放大相时的闭环增益。对于1.5bit结构,G=2。
OP增益指标的计算
假设运放的增益为A,且暂不考虑寄生电容Cp的影响, MDAC闭环时的反馈系数为β,由于运放带来的有限开环增益误差, 可以证明输出电压表达式为:
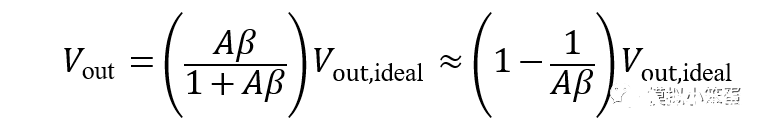
公式(1)
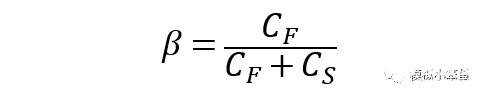
公式(2)
其中, 是Vout,ideal是理想的输出电压如下(具体参考:如何推导一个1.5位MDAC的输出函数?):
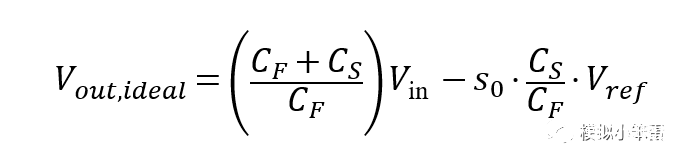
公式(3)
因此, 增益误差为:
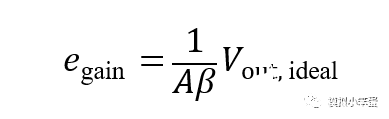
公式(4)
接下来我们将这个误差量折算到ADC的最前端,折算的方法是将该误差除以前向增益。根据前文的ADC架构图,设当前级为第i个流水级(i=1~M),折算到输入端的误差为:
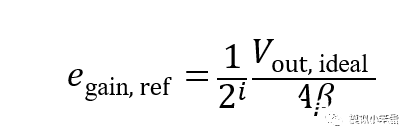
公式(5)
从MDAC传输曲线可看出,其最大输出摆幅是(3/4)*VFS(具体参考:如何推导一个1.5位MDAC的输出函数?)。计算时我们按VFS进行,则上述最大增益误差应该小于整体精度的1/2。则有:
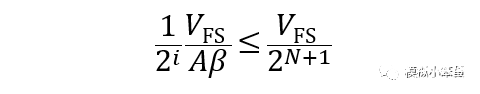
公式(6)
推出:
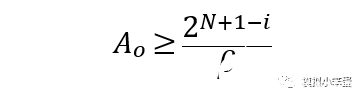
公式(7)
根据上式,假设一个9bit的ADC,我们尝试计算,结果如下表所示:
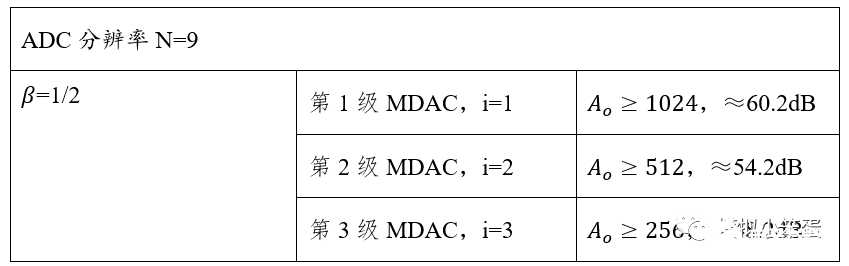
注意:
β值受Cp的影响,实际会小于1/2。因此考虑Cp影响后,因此实际要比表中的计算值更大。可以证明,只需要用代替上述公式中的β就可以得到考虑寄生后的表达式。
公式7也适用于S/H电路中OP的计算,但要取β=1,i=0。
审核编辑:黄飞
-
【SOC的多种计算方法】2024-06-05 5274
-
阻抗计算方法2013-06-10 3189
-
机器视觉计算方法2015-08-14 7916
-
Rstart的计算方法2021-10-29 2055
-
pcb载流能力的计算方法2008-03-06 1144
-
多传感器航迹融合的评价指标及计算方法2009-06-22 512
-
高频开关电源系统可靠性指标MTBF的计算方法2010-11-08 1043
-
IFFT的计算方法2008-10-30 14178
-
甲类单端的简易计算方法2016-01-19 1084
-
油藏数值模拟有限元并行计算方法研究_张允2017-03-20 1036
-
特征阻抗的计算方法2017-06-09 3030
-
公路坡度的表示和计算方法综述2021-08-11 1118
-
EMC计算方法和EMC仿真(1) 计算方法简介2023-02-14 4428
-
EMC计算方法和EMC仿真(1) ——计算方法简介2023-12-05 2890
-
模拟IC设计之OP带宽的计算方法2023-11-30 1803
全部0条评论

快来发表一下你的评论吧 !

