

图像处理算法——边缘检测
描述
图像处理领域中涉及很多特征,角点特征,边缘特征,形状特征,纹理特征,颜色特征,直方图统计特征等等(还有很多^_^)。这些特征有些是比较底层的特征,如角点特征,边缘特征,颜色特征等,有些则是较为高层的特征,如形状特征,纹理特征,直方图统计特征。
这里我们主要谈论底层特征中的边缘特征,提取这些特征的手段叫作边缘特征提取或叫作边缘检测。边缘检测常用的算子中分为一阶检测算子和二阶检测算子,这里提及的算子有些类似数学中的微分的概念(要有一定的数学基础哦)。边缘检测的另外一种形式也被成为相位一致性,这个概念我到后面再谈及,有了这个概念之后帮助我们从图像频域分析边缘提取这一过程。
表1 图像处理边缘检测算子分类表格
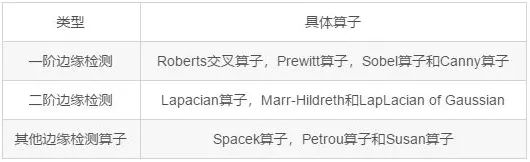
基于边缘检测的分析不易受整体光照强度变化的影响,同时利用边缘信息容易凸显目标信息和达到简化处理的目的,因此很多图像理解方法都以边缘为基础。边缘检测强调的是图像对比度。对比度从直观上的理解就是差异的大小,若对于灰度图像来说就是灰度值(亮度值)的差别,若对于彩色图像则是颜色的差异了。这些差异可以增强图像中的边界特征,因为这些边界就是图像对比度较大的体现。
这就是我们感知目标边界的大体机制,因为目标的表现就是与它周围的亮度差别。
一、水平差分算子、垂直差分算子
亮度变化可以通过对相邻点进行差分处理来增强。对水平方向的相邻点进行差分处理可以检测垂直方向上的亮度变化,根据其作用通常被称为水平边缘检测算子(horizontal edge detector),这样就可以检测出垂直边缘Ex;对垂直方向的相邻点进行差分处理可以检测水平方向上的亮度变化,根据其作用通常被称为垂直边缘检测算子(vertical edge detector),这样就可以检测出水平边缘Ey。
Ex = |Px,y - Px+1,y|
Ey = |Px,y - Px,y+1|
将水平边缘检测算子和垂直边缘检测算子结合,就可以同时检测出垂直边缘和水平边缘,即:
Ex,y =|Px,y - Px+1,y + Px,y - Px,y+1|
由此可以得到
Ex,y =|2 x Px,y - Px+1,y - Px,y+1|
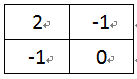
图1 一阶差分模板
利用泰勒级数分析可以知道相邻两点的差值是一阶导数的估算值,误差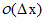 。
。
如果在相邻两个差分点之间插入一个像素来实现,相当于,相当于用两个相邻点的一阶差分作为新的水平差值Exx,其中
Exxx,y = Ex x+1,y + Ex x,y = |Px+1,y - Px,y + Px,y - Px-1,y| = |Px+1,y - Px-1,y |
利用泰勒级数分析可以知道一阶微分的估算值是由一个像素隔开的两个点的差值,误差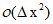 。
。
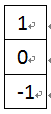
图2-1 改进的一阶差分模板My

图2-2 改进的一阶差分模板Mx
二、一阶边缘检测
(a) Roberts交叉算子
Roberts交叉算子实现的基础是一阶边缘检测,利用两个模板,计算对角线上而不是坐标轴上的两个像素的微分。这里命名这两个模板分别为M+,M-
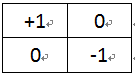
图3-1 Roberts交叉算子模板M+
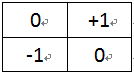
图3-2Roberts交叉算子模板 M-
(b) Prewitt边缘检测算子
边缘检测类似微分处理,它检测的变化的部分,必然对噪声和图像的亮度变化都有相应处理。因此,把均值处理加入到边缘检测过程中一定要非常谨慎。我们可以把垂直模板Mx扩展成三行,而水平模板My扩展成三列。这样就得到Prewitt边缘检测算子。
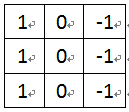
图4-1 Prewitt算子模板Mx
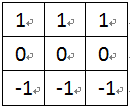
图4-2 Prewitt算子模板My
(c) Sobel边缘检测算子
如果把使两个Prewitt模板算子中心像素的权值去两倍的数值,便得到有名的Sobel边缘检测算子,它是由矢量方式确定边缘的两个掩码组成的。Sobel很受欢迎是因为它比Prewitt算子等同时期的其他边缘检测算子性能更好。

图5-1 Sobel算子模板Mx
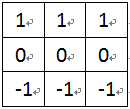
图5-2 Sobel算子模板My
Sobel算子的通用形式综合了一条坐标轴上的最优平滑和另一条坐标轴上的最优差分。值得注意的是,大的边缘检测模板的好处是它减少噪声的平滑效果更好,然而边缘模糊却成为一个大难题。
(d) Canny边缘检测算子
Canny边缘检测算子可以说是当前最受欢迎的边缘检测方法。它由三个主要目标形成:
无附加响应的最优检测
检测边缘位置和实际边缘位置之间距离最小的正确定位
减少单边缘的多重响应而得到单响应
Canny指出高斯算子对图像平滑处理是最优的。Canny边缘检测一般处理的步骤可以粗略的分为以下四个步骤:
应用高斯平滑处理
应用Sobel算子
应用非极大值抑制(非极大值抑制实质上是找到边缘强度数据中的最高点)
滞后阈值处理来连接边缘点(阈值处理需要两个阈值,即上限阈值和下限阈值 )
三、二阶边缘检测
一阶边缘检测的前提是微分处理可以使变化增强。找图像变化率最大的地方不仅可以通过一阶变化率的极值寻找,同时也可以通过二阶变化的过零点来寻找。
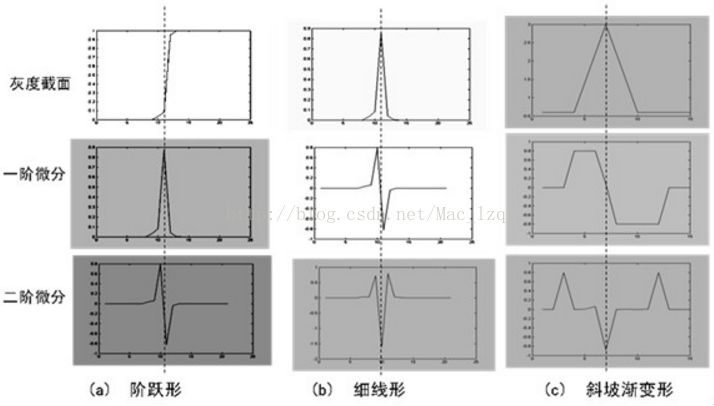
(a) Laplacian算子
二阶微分可以利用两个相邻一阶微分的差值来近似。这也和数学中的概念相一致。
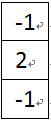
图6-1 垂直二阶模板
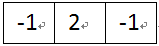
图6-2水平二阶模板
如果把水平二阶算子和处置二阶微分算子结合起来,可以得到一个全Laplacian模板算子。
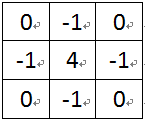
图7 Laplacian边缘检测算子
(b) Marr-Hidreth算子
Marr-Hidreth也是利用高斯滤波。该算子的曲面图是墨西哥帽子的形状,所以有时也被成为“墨西哥帽子”算子,如下图所示。
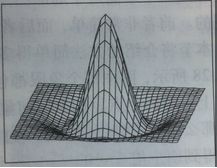
图 8 LoG算子的形状
实际上,如果把高斯平滑和Laplacian算子结合起来,可以得到一个LoG(Laplacian of Gaussian)算子,它就是Marr-Hidreth的基。
各算子的效果比较:
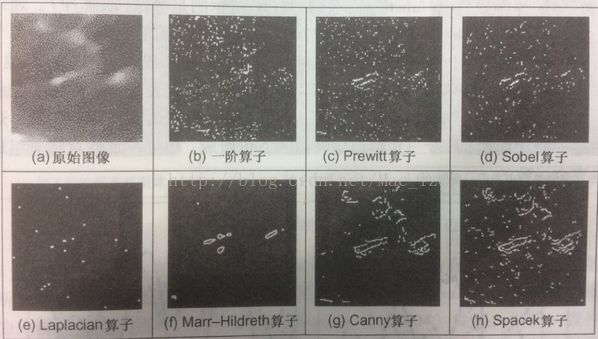
图 8 LoG算子的形状
四、其他边缘检测
边缘检测作为视觉处理的初级阶段,方法有很多种,这里我们再提及两个设计最优的边缘检测方法,Spacelk方法和Petrou方法。有兴趣的朋友可以进一步了解。这里需要提及的是Spacek算子使定位信噪比和峰值分离比的乘积最大化。Spacek算子比Canny算子具有很高的性能。Petrou算子使用的模板比较大,以便保存最优性,因此Petrou算子可以处理比较大的计算复杂度,但在使用的时候,应当具体问题具体分析。
五、相位一致性
边缘检测算子的比较突出了它们的一些内在问题:不完整轮廓问题、阈值选择问题和噪声响应问题。因为光照强度在图像的不同区域是不一样的,选择单个阈值通常不能适用于图像中的所有区域。这些问题单靠简单初级的处理难以解决。需要优化方法或者使用较为高级的手段才能达到一定的效果。
相位一致性(Phase congruency)方法是一个特征检测算子,它由如下两个优点:
可以检测大范围的特征
对局部(和平滑)光照变化具有不变性
这两个优点其实就是一致性检测具有局部对比度不变性:即使阶梯边缘强度变小,其变化位置并不改变。
-
基于FPGA的实时边缘检测系统设计,Sobel图像边缘检测,FPGA图像处理2024-05-24 3338
-
基于FPGA的边缘检测和Sobel算法2017-11-29 12227
-
如何利用FPGA实现Laplacian图像边缘检测器的研究?2019-07-31 2464
-
Labview图像处理——边缘检测2020-12-01 6695
-
常见图像传统处理算法是什么?2021-09-28 1592
-
虹膜图像预处理算法2010-01-13 752
-
基于Simulink的视频与图像处理算法的快速实现2010-04-29 822
-
医学图像边缘检测算法的研究2010-07-05 896
-
DSP6748图像处理算法2016-05-19 1200
-
基于DM642的红外测温与图像处理算法研究2017-02-07 1271
-
有趣的图像处理算法2018-01-12 5165
-
图像处理算法的优化2018-11-29 3690
-
机器视觉工业缺陷检测常用的图像处理算法2021-06-15 8400
-
单片机车道线检测模型(4)——图像处理算法2021-11-16 715
-
FPGA图像处理算法有哪些2023-09-12 1727
全部0条评论

快来发表一下你的评论吧 !

