电池工作温度如何影响电池性能？

过去的研究表明，材料/电解液界面稳定性对于电极材料在电池中性能发挥有着重要的影响。电极材料在电池循环充放电过程中往往会发生破裂产生微裂纹甚至最终粉化，加剧电极材料的降解，德国乌尔姆大学Orkun Furat教授等人利用超分辨显微图像技术量化了工作温度对于电池电极开裂的影响，重点探讨工作温度对于锂离子电池正极微结构的降解的影响。使用超分辨技术对SEM图像进行处理提高图像的分辨率和清晰度，进而对超分辨图像数据进行分割，实现定量的结构表征。

研究在不同的工作温度（20 ℃、30 ℃、40 ℃和50 ℃）下对经过200次6C(10 min) 充电循环的LixNi0.5Mn0.3Co0.2O2 (NMC532)进行特征分析，获取了扫描电子显微镜（SEM）图像，确定结构描述符（如：单颗粒的全局粒子孔隙率、裂纹的尺存以及比表面积分布等参数），利用立体形态学方法研究研究局部颗粒孔隙率与颗粒中心距离的关系。研究结果表明：随着循环温度的升高，颗粒孔隙度增大;颗粒孔隙率在颗粒中心处最大，沿颗粒半径向外逐渐减小。在四种循环温度老化条件下，颗粒表面积相似。通过此研究，可以更好地理解电池工作温度对于电池性能的影响，为改进电池电极材料设计和使用提供参考。

相关研究成果“Quantifying the impact of operating temperature on cracking in battery electrodes, using super-resolution of microscopy images and stereology”为题发表在Energy Storage Materials上。

【研究背景】

多晶正极材料的结构退化是限制锂离子电池寿命的影响因素之一，微观结构图像的定量分析有助于锂离子电池的降解物理学的理解，并为验证电化学-机械降解模型提供数据。微/纳米计算机断层扫描(CT)或聚焦离子束(FIB)为基础的成像技术方法对于材料的微观结构表征是非常有价值的。通过成像技术获得数据确定高级结构描述符，详细地了解材料的微观结构信息，从图像信息可以识别单颗粒，通过计算其尺寸与形状获取描述符以及描述符的分布。通过将结构描述符与其他参数的相关联就可以量化不同的参数对于材料微观结构的影响（例如微观结构-性能关系或工作参数对微观结构的影响）。同时，实验获得的图像的结构特征可以用来调整物理模型中的未知参数，用于宏观性质的数值模拟。

目前，三维成像技术（CT）成本高昂，无法对材料的微观结构进行表征。基于二维图像技术的三维形态学定量分析比较困难。但是，这种差异可以利用立体学方法校正，立体学领域涉及从低维观测(如平面剖面)确定三维结构的几何特性。然而，从平面剖面计算粒度分布比较困难。

这篇文章研究电极材料在不同工作温度下循环并在平面切片中成像来表征锂离子电池电极的微观结构，定量分析了裂纹演化与正极活性物质损失之间的关系。采用超分辨技术通过对图像预处理，提高图像分辨率（图1，上行右），识别正极颗粒内的裂纹等精细特征。然后，对超分辨率图像数据进行相位分割，分割为背景、固相、裂纹相计算循环正极材料的描述符（如全局颗粒孔隙率等）, 量化正极材料不同相的特征。从获得的结果以识别单个裂纹，允许计算每个观察到的裂缝的形态描述符(大小，长度和宽度)。这样的描述符(或其分布)允许对循环条件对结构退化的影响进行更深入的研究。通过结合颗粒分割和相位分割(提供有关裂纹位置的信息)，甚至可以确定单个颗粒的孔隙率等进一步的描述符（图1，第二行左）。此外，本文提出了一种计算局部粒子孔隙度的方法，该方法是粒子和相位分割到粒子中心距离的函数（图1，最后一行左）。通常在SEM图像数据中只能看到具有分散尺寸的近球形NMC颗粒的横截面，不清楚横截面相对于颗粒中心的高度，因此无法确定横截面内某一点到颗粒中心的确切距离。为了克服这个问题，我们使用了立体学的方法来估计横切面图像数据的距离。

图1. 循环正极表征的工作流程。首先，使用生成对抗网络，在不同工作温度下循环的正极的SEM图像数据(上行，中心)进行超分辨处理(上行，右)。虚线绿色的方格在绿色的实线方格内以2倍的放大倍率显示。使用卷积神经网络，从超分辨率数据中确定相位分割(第二行，右)。这允许区分背景(黑色)，固相(灰色)和裂纹相(白色)。通过应用传统的图像处理技术(即分水岭变换)，可以在裂纹相内确定裂纹的分割(第二行，中心)，从而识别单个裂纹。为了可视化，固相用灰色表示。此外，可以为固体相和裂纹相的结合计算颗粒分割(第二行，左)，这样就可以识别单个颗粒。请注意，小颗粒已从随后的分析中去除。最后，从这三个部分确定了量化结构退化的各种描述符(最下面一行)。

【核心内容】

图像数据预处理

第一步将图像进行相分割，分割为背景、固相以及裂纹相（图1，第二行右），采用以下形式：

像素值0、1、2分别以黑色、灰色和白色表示，通过分割后的结果计算相的总面积或它们的分数(例如，整体颗粒孔隙率)，从而量化NMC颗粒结构降解的总体程度。然而，相位分割不允许我们识别图像数据中的单个裂纹。因此，需要将裂纹相位划分为与单个裂纹相关的像素集，进一步识别图像中单个裂纹。

第二步将图像中裂纹相划分与单个裂纹相关的像素集（图1，第二行中），采用以下形式：

第三步将通过将粒子和裂纹相的联合集划分为与单个粒子相关的像素集以定量识别分析单个颗粒的微观结构（图1，第二行左），采用以下形式：

其中每个已识别的粒子以随机选择的颜色显示。然后，根据颗粒分割确定每个颗粒的孔隙度值，从而确定颗粒孔隙度的概率分布。

图像超分辨处理

训练神经网络执行超分辨率，即人为地增加低分辨率图像的分辨率，从而在保持原始视场的情况下获得与高分辨率图像相同的分辨率。采用生成对抗网络改善分割结果（SRGAN）。根据给定信息，训练SRGAN用于超高分辨路图像重构，通过训练生成器网络GθG和判别器网络DθD将低分辨率图像数据进行超分辨率处理，将高分辨图像进行清楚的裂纹识别。θG和θD代表可训练参数，分别取值于参数空间ΘG和ΘD。生成器GθG的训练任务是调整其可训练参数，使得输出图像̂̂I = G θG (I low )在感知损失函数（perceptual loss）的指导下，在超分辨率任务中表现更好。文中提到使用了Python的TensorFlow软件包来实现SRGAN架构，并利用随机梯度下降方法Adam对生成器GθG和判别器DθD进行交替训练。已知信息中还展示了SRGAN的生成器和判别器的网络架构示意图，分别在图2a和图2b中可见。

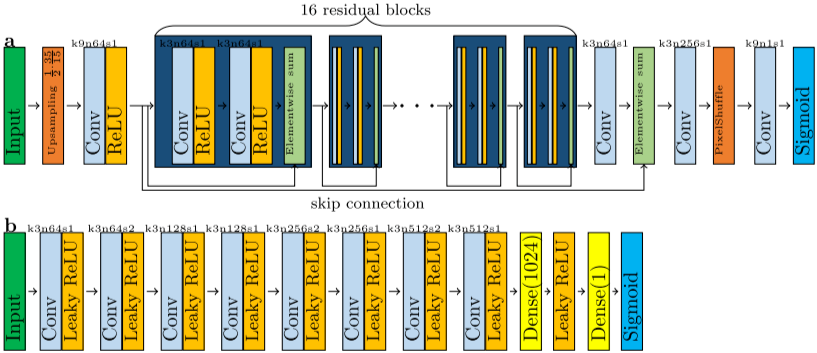
图2. SRGAN。用于执行超分辨率的发生器(a)和鉴别器(b)的体系结构。卷积层数用Conv表示，表示内核大小、特征图个数和步长，如k9n64s1表示内核大小为9、特征图个数为64、步长为1的层。

相位和裂纹分割

使用名为modular U-net的卷积神经网络确定相位分割，其U深度为5，第一个卷积层有32个滤波器。U-net的输出层包含三个通道，使用softmax函数作为激活函数，用于将超分辨率图像中的像素分类为背景、固相和裂纹相。网络的输出Ŷ经过阈值处理，得到相位分割的结果S，其中阈值t用于控制具体的分类策略。

采用以下形式进行分相：

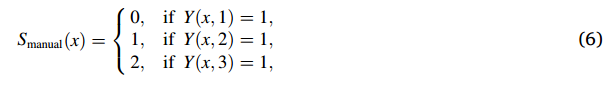
其中x ∈ W，W→{0, 1, 2}。训练过程中每个训练步骤中都会随机选择一对大小为1024×1024像素的训练数据(I, Y)进行训练。在连续进行了200个训练步骤后，使用从验证数据中随机选择的50对切割图像计算加权分类交叉熵来确定验证损失。类似于上述描述的验证过程，如果验证损失不再改善，训练过程将被终止。验证损失是通过计算50对从验证数据中随机选择的切割图像的加权分类交叉熵来确定的。这意味着将每个预测图像与相应的标签图像进行比较，并根据其分类结果计算损失。训练的目标是使验证损失最小化，以提高生成器对低分辨率图像的超分辨率性能。如果在连续的性能检查中，验证损失不再改善，则训练过程将被终止。这可以视为一种早停策略，以防止训练过程陷入过拟合状态。训练完成后，U-net会部署在所有超分辨率图像I上。其输出是三通道图像Ŷ : W × {1,2,3}→[0,1]，其中Ŷ(x,1)、Ŷ(x,2)、Ŷ(x,3)可以被解释为网络确定像素x分别位于背景、固相或裂纹相的确定度。这种“模糊”分割需要进一步处理以得到满足等式(1)中相位分割定义的图像。具体处理过程可能涉及阈值处理和其他后处理步骤，以确保生成的分割图像满足特定的相位分割定义。这可能包括对网络输出的模糊分割进行硬化，将分割结果转化为清晰的类别标签，以及进行其他必要的调整以满足相位分割的要求。

从网络的输出Y，通过Y，得到相位分割S: W→{0,1,2}：

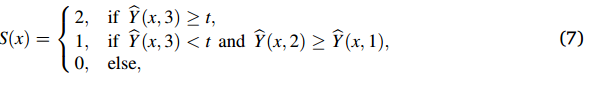
粒子级分割

进一步，通过将粒子级分割与相位级分割结合起来，可以计算出用于每个固体和裂纹相位的粒子级分割。这样，可以识别出每个粒子。值得注意的是，在后续分析中，可能会从数据中去除小颗粒。通过这三个分割结果（相位级分割、裂纹级分割和粒子级分割），可以计算出各种描述符，例如各个粒子的孔隙率。具体到粒子级分割的计算方法，可以使用基于标记点的分水岭转换（marker-based watershed transformation）。这种方法可以被看作是一种区域生长算法，用于划分二值图像中的区域。通过这样的粒子级分割，我们可以获得一个满足等式（3）的粒子级分割方案Sp：W→{0,1,⋯, np}，如图1中的第二行左边所示。

相、裂纹和颗粒的形态学描述符

整体颗粒孔隙率和裂纹强度

为了表征裂纹的总体数量，通过将裂纹相的面积除以在相位分割S(1)，...，S(m)中观察到的裂纹和粒子相的并集的面积来确定全局粒子孔隙度ρ。具体来说，通过计算与相应相位相关的像素数量来计算这些区域。即，全局粒子孔隙度ρ是通过以下公式进行计算：

另一个聚合描述符是表征裂纹频率的裂纹强度λ，通过以下公式计算：

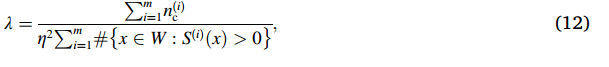
式中η = 14.3nm。

单个裂缝的大小和形状

通过裂纹级分割观察到的每个裂纹，可以计算用于表征个体裂纹的进一步形态学描述符。这些描述符提供了比之前考虑的聚合描述符更详细的对阴极材料结构退化的观察。这些描述符可以包括裂纹的大小、长度和宽度等形态学特征。通过计算这些描述符（或其分布），可以更深入地研究循环条件对结构退化的影响。

利用面积等效直径d表征描述裂纹的尺存：

由于每个分割的裂纹C与通过骨架化裂纹相得到的离散化曲线L⊂W相关联（参见第2.3.2节），将裂纹长度ℓ定义为观察到的曲线L的长度：

对于离散化曲线L的每一个像素点x，可以确定以x为中心，且其圆盘完全被裂纹相包含的最大半径r disk (x)。具体来讲，r disk (x)是满足S(y)<2的所有y点与x的欧几里得距离的最小值，即：

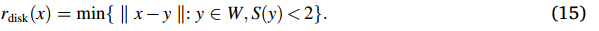
通过平均这些局部裂纹宽度，可以得到裂纹宽度b：

计算在裂缝分段S(1) c，⋯，S(m) c中观察到的每个裂纹的描述符向量(d, r, b)，这样就得到了在20 ℃循环的阴极的裂纹描述符向量的样本x20，其形式为：

其中n20 > 0表示在S(1) c ，⋯， S(m) c中观察到的裂纹的总数。

单个颗粒参数描述

通过粒子级分割Sp和相位级分割S，可以得到关于粒子的更详细的信息，而不仅仅是简单的全局粒子孔隙率。这些描述符可以提供关于粒子自身的特征，例如粒子的形状、尺寸、位置等，有助于更全面地了解阴极材料中的裂纹状况以及与粒子属性的关系。包括单个颗粒的比表面积和孔隙率描述符、局部颗粒孔隙率描述符的确定。

【讨论内容】

以不同循环温度（20 ℃、30 °C、40 °C和50 °C）正极的电化学分析和结构裂纹特征表征结果为基础。利用增量容量（IC）分析和深度学习（DL）模型评估了衰老模式、锂储量丧失（LLI）和活性材料丧失（LAM）。与传统的IC方法不同，传统方法是通过调整LLI和LAM，将C/20模拟的IC曲线与实际获取的IC曲线进行单独比较。通过基于合成数据的深度学习模型，可以快速自动地量化评估衰老模式。图3提供了包括所有可能情况的合成IC数据，包括电极活性物质的丧失和锂储量的丧失。

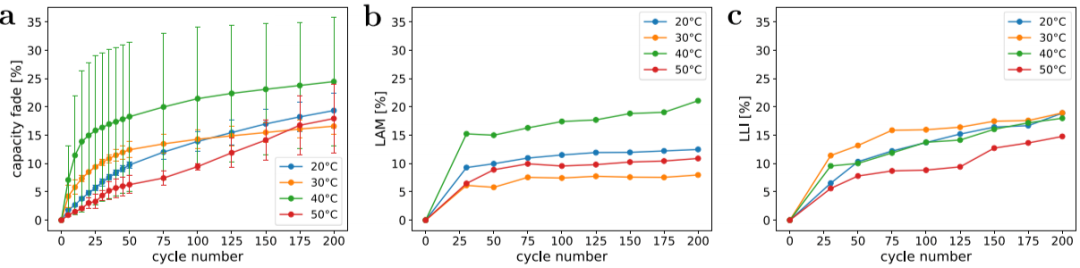
图3. 电化学分析。(a)容量衰减，(b)正极活性材料损耗，(c)锂库存损耗与循环次数的关系。所有数据都基于C/20容量测量。(b)和(c)为增量容量分析所得。

在描述符基础上，所正极进行了结构表征。例如，根据在20 °C下循环的阴极的SEM图像，我们通过使用方程(11)确定了全局粒子孔隙率ρ = 0.0852，通过使用方程(12)确定了裂纹强度λ = 0.241μm ^-2^ 。对于在30 °C、40 °C和50 °C下循环的阴极，相应的全局粒子孔隙率和裂纹强度值列在表1中。

表1 不同循环条件下阴极整体颗粒孔隙率ρ和裂纹强度λ的平均值和标准差

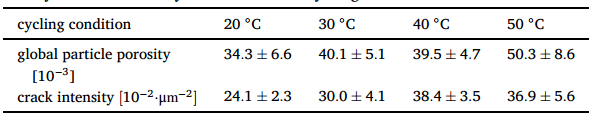
图4a展示了不同循环条件（20 °C、30 °C、40 °C和50 °C）下裂纹大小的箱线图。类似地，图4b和4c分别展示了裂纹长度和宽度的箱线图。需要注意的是，各种循环条件下观察到的裂纹数量分别为：n20=8733，n30=11212，n40=17866，n50=21242。使用调整后的数据集X̃j(j ∈ {20, 30, 40, 50})确定了对应的箱线图，其中省略了具有较小裂纹尺寸的描述符向量。详细的分析结果和解释可能需要参考原文或其他相关资料，图4d-f可作为参考。

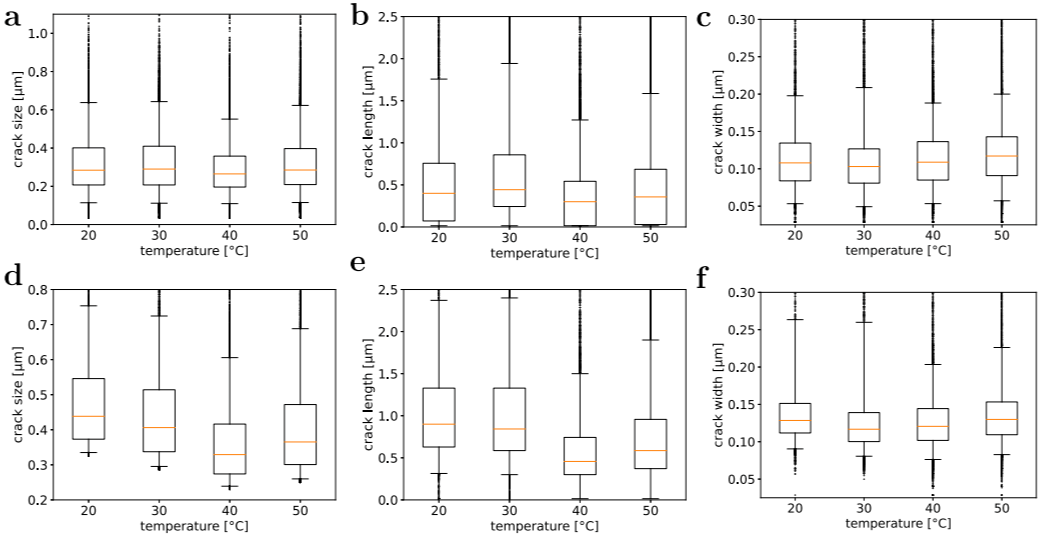
图4. 对于每个循环条件j∈{20,30,40,50}，从数据集X~ j~计算得出的裂缝尺寸(a)、长度(b)和宽度(c)的箱形图。方框的底部和顶部表示第一和第三个四分位数。中位数用框内的红线表示。须线表示第5和第95百分位数，而点表示异常值。对应调整后的数据集X̃j计算得到的裂纹大小、长度和宽度的箱线图在(d)-(f)中展示。

基于给出的结构特征表征，观察到全局粒子孔隙率随着操作温度的增加呈单调增加的趋势，具体数据见表1。温度对粒子孔隙率的单调影响也可以在粒子孔隙率的分布图中观察到，具体可参考图5a。与此相反，裂纹强度在操作温度上仅“大多数情况下”呈单调增加的趋势，除了40 ℃下的循环条件，具体数据见表1。此外，从图4a-c和图5b可以看出，温度似乎对裂纹的尺寸/长度/宽度没有显著影响。综上所述，根据结构特征表征的结果，操作温度对阴极的降解具有显著影响。全局粒子孔隙率显示出与温度的单调关系，而裂纹强度则在大多数情况下随温度的增加而增加。这些结果表明，操作温度是影响阴极结构降解的重要因素。然而，温度对裂纹的尺寸/长度/宽度的影响似乎不是非常明显。

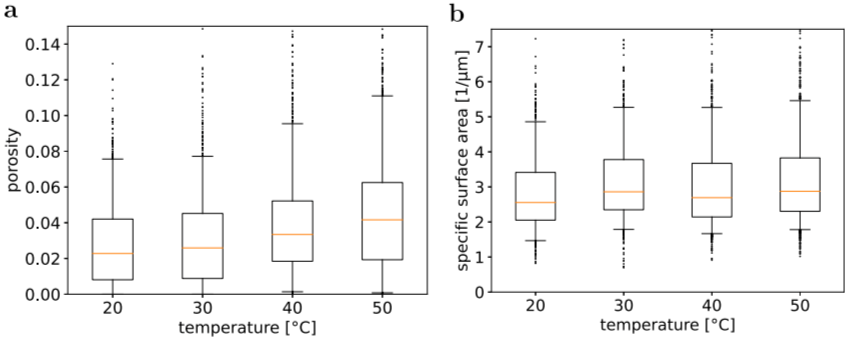
图5. 每个循环条件j∈{20,30,40,50}，由数据集zj计算得到的颗粒孔隙度(a)和比表面积(b)箱形图。方框的底部和顶部表示第一和第三个四分位数。中位数用框内的红线表示。须线表示第5和第95百分位数，而点表示异常值。

当考虑裂纹扩展的影响时，只考虑大裂纹，观察到裂纹宽度和长度随着温度从20 ℃到30 ℃以及从30 ℃到40 ℃的升高而总体下降，然而，从40 ℃到50 ℃，观察到裂纹宽度和长度的增加，见图4d,e。同样，当只考虑大裂纹时，随着温度的升高，裂纹宽度先减小后增大，如图4f所示。在图6中，观察到从颗粒外部到颗粒中心的局部孔隙率单调增加，同样，对于在40 °C循环的阴极，这种观察结果并不明显。40 °C的数据是颗粒损伤和容量衰减趋势的异常值。增量容量分析(图3)显示，40 °C老化电池异常高容量衰减的原因是由于阴极活性物质的过度损失。其原因尚不清楚。从进一步讨论温度损伤趋势中省略了40°C的数据。

对温度上升时颗粒孔隙率增加的可能原因提出了两个假设。首先，由于较快的传输和动力学过程，高温下的电池可以更好地接受电荷，并在每个循环中经历更大的ΔSOC波动。高温下的电池还经历较少的容量衰减，因此可以在其寿命周期的大部分时间内维持较大的ΔSOC。在高温下，较大的ΔSOC波动会引起较大的体积变化，可能增加了颗粒断裂和孔隙的程度。高温下颗粒孔隙率增加的第二个可能原因是由于机械性能随温度的软化。例如，复合正极的拉伸测试表明，在20 ℃和80 ℃之间，复合正极的最大拉伸应力降低了25%，断裂应变降低了55%。

由图5可知，颗粒中心处局部孔隙率最大。这一观察结果与全电池的高倍率充电(正极颗粒的快速衰减)相反，对于均匀颗粒，预计会导致阴极颗粒外部区域出现更多裂纹。对于非均相多晶颗粒，裂纹模式更为复杂。高倍率的充放电也可能导致颗粒中心附近的优先开裂，但目前的电池是在较低的C/2倍率下放电。在颗粒中心附近观察到的优先开裂的其他原因包括制造压延步骤产生的应力/应变和上述或ΔSOC(体积)变化引起的应力/应变，与快速充电速率无关。

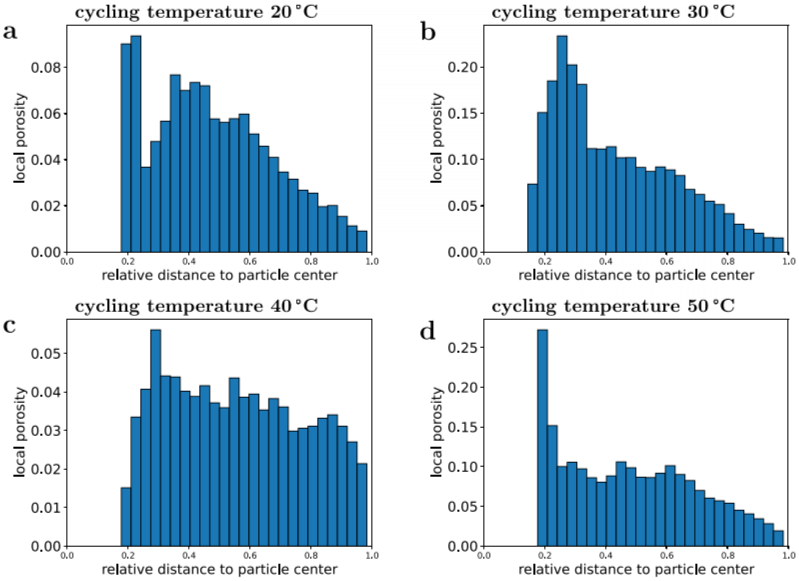
图6. 在20 ℃ (a)、30 ℃ (b)、40 ℃ (C)和50 ℃ (d)循环的正极，局部孔隙度与粒子中心距离的函数关系。

【结论展望】

综上所述，本文利用扫描电镜图像定量分析了锂离子正极在不同工作温度下的结构退化。为此，为了改善分割结果，部署了一个生成对抗网络来解析数据。分割数据的结构表征包括总体颗粒孔隙率和裂纹强度等描述符的聚合，以及各种裂纹和颗粒描述符的分布。此外，利用立体学方法计算了局部颗粒孔隙度作为到颗粒中心距离的函数。为电子显微成像技术在推进材料领域的研究提供了新的方法和见解。

审核编辑：刘清