功率增益、有损元件和级联系统的噪声系数讲解

噪声系数的概念相当直观，即描述信号通过元件时信噪比（SNR）下降的情况。然而，噪声系数的定义中隐藏着一些微妙之处，而这些微妙之处有时却没有得到足够的重视。必须充分理解的一个复杂因素是，噪声系数值是在 290 K 标准温度下，针对已知源电阻（通常为 50 Ω）指定的。

在本文中，我们将讨论另一个重要的微妙之处，即噪声系数定义中使用的功率增益类型。随后，我们将探讨有损元件和级联系统的噪声系数。

重新审视噪声系数定义和信噪比

噪声系数 (F) 定义为 输入端SNR 与输出端 SNR 之比：

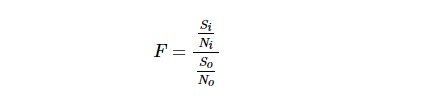
（公式 1）

其中：

Si和So是电路输入和输出处的可用信号功率

Ni和No是输入和输出处的可用噪声功率代入So=GASi可得到以下替代方程：

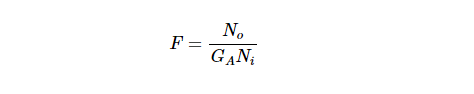
其中GA是电路的可用功率增益。

接下来，让我们来看看可用功率增益的定义。

使用阻抗的模块的可用功率增益

图1说明了如何计算给定源阻抗ZS=RS+jXS下模块的可用功率增益。

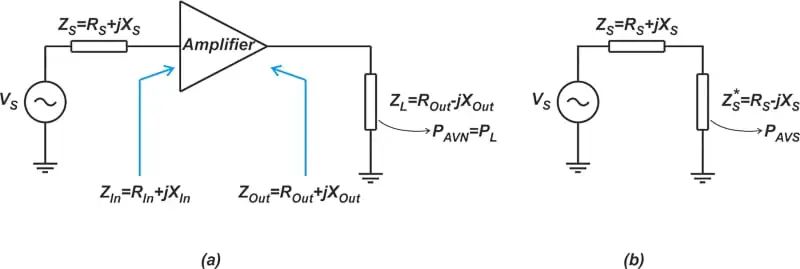
（图1:显示给定电源阻抗下模块功率增益的图表）

假设模块的输入和输出阻抗为ZIn=RIn+jXIn且Zout=Rout+jXout。如图1（a）所示，我们可以将模块输出连接到共轭匹配负载，即ZL=Rout-jXout，并测量输送到负载的功率PL。由于输出是共轭匹配的，因此PL是来自网络PAVN的可用功率。

所需的另一个电量是源PAVS的可用电量。如图1（b）所示，这是源向ZS的复共轭物传递的功率。PAVN与PAVS的比值定义为模块GA的可用功率增益：

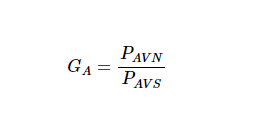
可用增益取决于ZS，而不是ZL。这是因为根据定义，负载阻抗是模块输出阻抗的复共轭匹配，因此已经由模块的输出阻抗设置。请记住，可用增益说明了DUT（被测器件）的源和输入之间的不匹配。

在噪声系数定义（等式1）中，Si是信号源的可用功率，So是可以输送到匹配负载的输出功率。因此，比值So/Si满足可用功率增益的定义。请记住，在射频工作中有几种不同的功率增益定义，例如换能器功率增益和插入功率增益。如果我们在NF计算中使用除可用增益之外的功率增益，我们将获得实际NF值的近似值。例如，实际的噪声系数测量方法通常确定DUT的插入增益。使用插入增益而不是可用增益可能会在我们的噪声系数测量中引入误差。

还值得一提的是，在处理级联级时，可用增益是有用的。级联的总可用增益等于单个可用增益的乘积。为了找到级联的可用增益，应为等于前一级输出阻抗的源阻抗指定每个级的可用增益。

有损分量的噪声系数

在设计射频系统时，我们有时会发现有必要在信号链的特定点引入损耗。例如，在测试和测量应用中，我们可以通过衰减器降低失配不确定性。衰减信号的无源电路必须具有物理电阻，我们知道电阻器会产生热噪声。因此，无源衰减器会降低 SNR 性能。让我们看看如何确定这些组件的噪声系数。例如，考虑为50Ω系统设计的6dB T型衰减器，如下所示（图 2）。

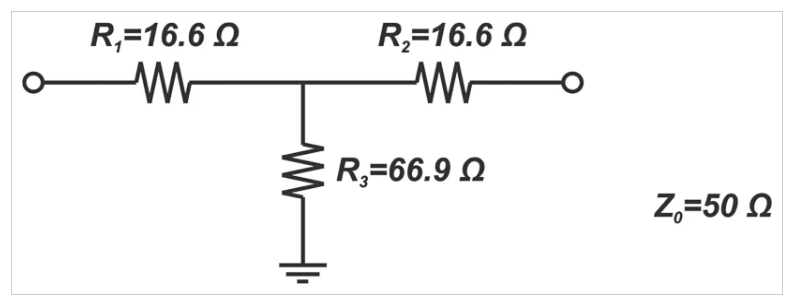
（图2:为50Ω系统设计的6 dB T型衰减器的示例图）

我们可以按照一般程序并通过执行噪声分析来确定该电路的噪声系数。该方法涉及一些繁琐的计算。更有效的方法是考虑电路的戴维宁等效值。衰减器输出端的可用噪声是来自衰减器戴维南电阻的可用噪声。作为一般规则，如果无源（互易）网络的两个端子之间出现的戴维南电阻等于 Rth，则这些端子之间出现的热噪声的PSD由下式给出

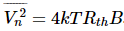
在我们的示例中，衰减器设计用于50Ω系统。添加输入和输出终端，我们得到如图3 所示的原理图。

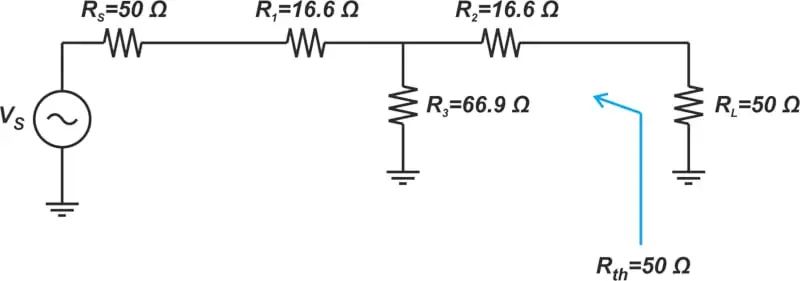
（图3：显示 50Ω衰减器以及输入和输出终端的图表）

根据设计，输出阻抗Rth等于系统的参考阻抗，即Rth=50Ω。由于Rth等于源阻抗Rs，因此衰减器输出端可用的噪声功率等于源阻抗 Rs提供的噪声功率（我们隐含地假设衰减器和 Rs 处于相同温度）。这意味着衰减器输入和输出处的噪声功率相同，即等式1中的Ni=No，从而得出：

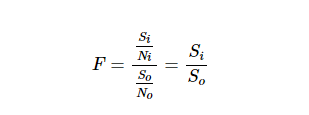
另一方面，我们知道衰减器按其指定值衰减输入信号功率。例如，对于6dB衰减器，Si比So大6dB。考虑到这一点，上述方程表明6dB衰减器的噪声系数为6dB。通常，如果无源衰减器的物理温度为T0=290K，则其噪声系数（dB）等于其损耗（dB）。

如果我们分析图3中的电路，我们会发现Rs产生的噪声在通过衰减器时衰减了6dB。然而，电阻器R1、R2和R3对电路输出贡献刚好足够的噪声，使得衰减器的输入和输出处的总可用噪声是相同的。

如果衰减器处于任意温度怎么办？

上述讨论仅适用于衰减器处于T0的情况。如果衰减器处于任意温度T，我们可以首先考虑衰减器和源电阻都处于T的情况。通过分析这种情况，我们可以确定衰减器 No(added) 添加的噪声，并可以使用这些信息来找到噪声系数。让我们以图3中的电路为例进行检查。如果包括Rs在内的整个电路处于T，那么输出No处的可用噪声功率等于Rs的噪声功率（我们知道它是kTB）：

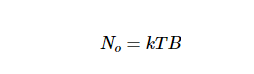
我们可以通过另一个等式找到总输出噪声No：

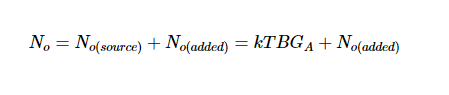
其中：

• No(source)是源于源阻抗的输出噪声的一部分

• No(added) 是衰减器添加的噪声

• GA是块的可用增益

结合这些方程，我们可以找到 No(added)  = kTB(1-GA)。现在，如果我们假设 Rs处于噪声系数定义指定的标准温度T0处 ，则T处有损组件的噪声系数为：

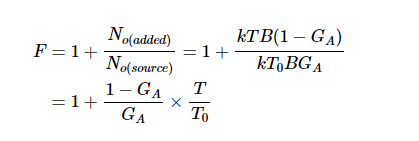
对于衰减器，损耗L等于1/GA，并且上述方程可以稍微简化为：

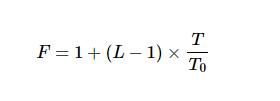
在T=T0的特殊情况下，我们得到 F = L

级联系统的噪声系数

虽然我们通常单独表征电路块，但我们最常用它们作为级联系统的组成块。因此，根据单个块的噪声系数规范来确定整个系统的噪声性能是很重要的。考虑一个由N个双端口设备组成的级联系统，如图4所示。

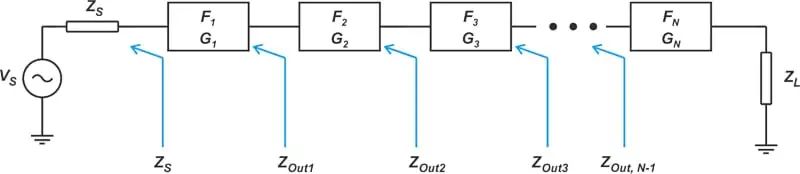
（图4：由N个双端口设备组成的级联系统示例）

在上图中，Fi和Gi表示第i级的噪声因子和可用功率增益。级联系统的噪声因子可以通过应用以下方程（称为Friis’ 方程）来找到：

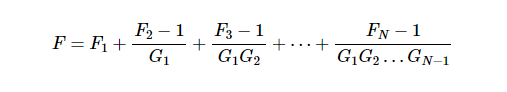
注意，在上述方程中，Fi和Gi项都是线性（而不是对数）量。根据Friis的公式，每个级的噪声因子除以该级之前的总增益。因此，后期阶段对整体表现的影响较小。这意味着第一阶段对整个系统的噪声系数有重大影响。

在处理Friis方程时，应该注意的是，每个级的噪声因子应该指定为其前一级的输出阻抗。例如，参考图4，第二级的噪声因子F2应该指定为Zout1的源阻抗，F3对应于Zout2的源阻抗等等。让我们看一个例子来澄清上面的一些概念。

示例：查找无线接收器前端的噪声系数

求以下无线接收器前端的噪声系数，如图 5 所示。

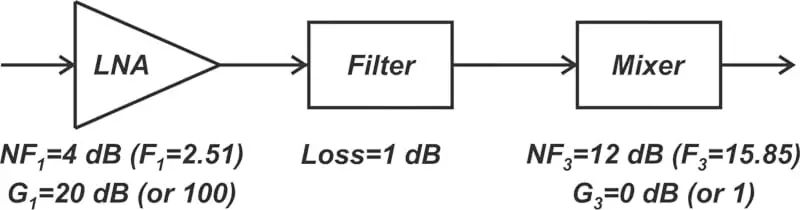
（图5：来自终端系统的无线接收器示例）

LNA和混频器的噪声因子和增益也如图所示。此外，滤波器的损耗为1dB。我们知道，无源衰减器的噪声系数（dB）等于其损耗（dB）（假设物理温度T0=290K）。因此，对于过滤器，我们有：

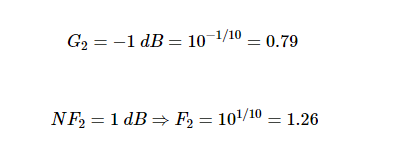
应用Friis’s 方程，我们得到：

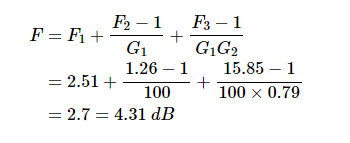
尽管混频器本身具有F3＝15.85，的大噪声因子，但添加滤波器和混频器会使总噪声因子增加相对较小的值，从2.51增加到2.7。滤波器和混频器的贡献较小，因为在这些分量之前有相对较大的增益。

　　审核编辑：汤梓红