

IGBT稳态分析—电流与电荷分布的初步分析(1)
电子说
描述
IGBT作为大功率双极型开关器件,持续工作在大注入、低增益的状态下,关断过程中因为电子电流、空穴电流关断不同步,使得IGBT在关断的瞬态下载流子浓度分布会发生较大变化,导致器件同时受到大电压和大电流的冲击,这是IGBT所特有的一种性质,而关断瞬态失效也是IGBT最常见的器件失效形式。
基于第五章对IGBT物理结构模型的构建,本章将尝试着对IGBT的瞬态,特别是关断瞬态进行深入分析。
本章梳理过程中需要涉及到较多的数学推导过程,笔者尽量将推导逻辑讲清楚,对于具体的推演过程,读者可根据情况选择性阅读。
首先对瞬态(Transient state)做一个基本的定义,瞬态描述的是电流、电压、电荷等物理量随时间t变化过程;与瞬态相对应的状态为稳态(Steady state),稳态过程中上述物理量不随时间t变化。IGBT的导通状态可以近似认为是稳态,而关断过程则近似认为瞬态。
鉴于电压是电场的积分,电场是电荷的积分,而电流是电荷在时间上的微分,所以本质上我们可以用电荷分布随时间的变化来来建立电压、电流等与时间之间的关系,即若能准确地推演出电荷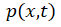 随时间的数学关系
随时间的数学关系 ,即可对瞬态进行准确的数理描述。
,即可对瞬态进行准确的数理描述。
如前所述, IGBT工作在大注入状态下,大注入成立的前提是N-base区域中的少子浓度远大于衬底浓度,即 ,因此只要分析清楚
,因此只要分析清楚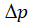 空间分布(为简化推导过程,这里只考虑一维状况)随时间的变化函数
空间分布(为简化推导过程,这里只考虑一维状况)随时间的变化函数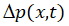 即可,这需要根据边界条件求解电荷的扩散方程。在《IGBT中的若干PN结》一章中,我们已经对少子的扩散方程做过详解,推导了
即可,这需要根据边界条件求解电荷的扩散方程。在《IGBT中的若干PN结》一章中,我们已经对少子的扩散方程做过详解,推导了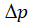 随时间和空间的数学关系,为方便后续理解,这里大致回顾如下:
随时间和空间的数学关系,为方便后续理解,这里大致回顾如下:
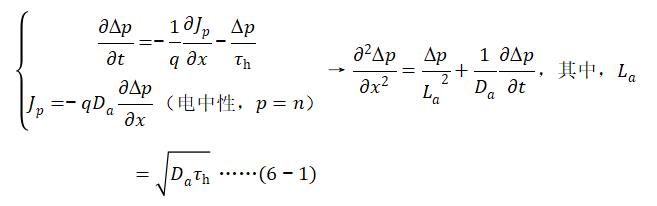
根据不同的边界条件,求解该扩散方程,即可得到相应的多余载流子(少子)浓度分布。欲准确计算关断瞬态的扩散方程,就必须首先得到扩散方程的初始状态值(t=0),作为其时间维度上的边界条件,而t=0的状态对应的是导通状态,即稳态,所以稳态是瞬态的初始状态。
因此必须先对稳态进行准确的分析。对于稳态, ,扩散方程(6-1)简化为,
,扩散方程(6-1)简化为,

因为IGBT的大注入特性,电子和空穴的运动相互影响,这个关系用双极性扩散系数来描述。
-
导体静电平衡状态的基本特征和电荷分布2024-02-26 7925
-
IGBT稳态分析—电流与电荷分布的初步分析(2)2023-12-01 1486
-
开关电源变换器稳态原理分析(电感伏秒平衡及电容电荷平衡)2022-01-07 1277
-
功率变换器中的功率磁性元件分布参数2021-11-09 3333
-
开关电源变换器稳态原理分析(电感伏秒平衡及电容电荷平衡)2021-11-07 900
-
网点电流法怎么解决这个RL电路交流暂态和稳态分析?2018-09-21 3272
-
双馈风电机组变流器IGBT结温计算与稳态分析_李辉2017-01-08 1155
-
均匀传输线正弦稳态分析2009-07-27 1729
-
正弦稳态分析2008-12-04 1091
全部0条评论

快来发表一下你的评论吧 !

