

IGBT的关断瞬态分析—电荷存储变化趋势(1)
电子说
描述
现在我们把时间变量 加入,进行电荷总量
加入,进行电荷总量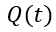 的瞬态分析。
的瞬态分析。
当栅极电压低于阈值电压,IGBT内部存储的电荷开始衰减,衰减过程是因为载流子寿命有限而自然复合,表达式如下:
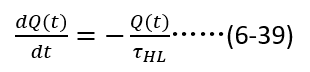
需要注意的是,在求解(6-39)的过程中,不能直接将(6-38)作为初始值,因为在关断的一瞬间,沟道电流的突然消失,即上一节中 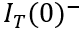 到
到 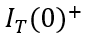 的变化,会导致IGBT体内电荷的突然减小,将电荷初始值记为
的变化,会导致IGBT体内电荷的突然减小,将电荷初始值记为 ,显然
,显然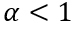 。
。 的具体数值取决于关断之前
的具体数值取决于关断之前 的大小,感兴趣的读者可以自行推导,这里不再赘述。(6-39)很容易积分求解,
的大小,感兴趣的读者可以自行推导,这里不再赘述。(6-39)很容易积分求解, 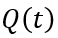 随时间
随时间 成e指数关系衰减,即
成e指数关系衰减,即

例如,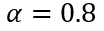 ,假设在
,假设在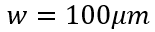 且保持不变的情况(关断过程显然不是这样,下面会再讨论
且保持不变的情况(关断过程显然不是这样,下面会再讨论 随时间变化)存储电荷衰减随载流子寿命变化的衰减趋势如图所示。
随时间变化)存储电荷衰减随载流子寿命变化的衰减趋势如图所示。

显然,随着载流子寿命的减少,电荷衰减速度加快。因为电流表征了电荷随时间的变化率(电荷的时间微分),利用(6-39)和(6-40),乘以系数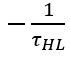 ,也就得到瞬态中电流随时间的变化关系。
,也就得到瞬态中电流随时间的变化关系。
在上一节中,我们定性地说明了在关断瞬间 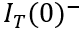 和
和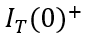 的突变,这里我们推导一下理论上这个变化究竟是多大。
的突变,这里我们推导一下理论上这个变化究竟是多大。
在关断瞬间,沟道夹断,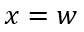 处的电子电流
处的电子电流 ,根据上一章的稳态分析中对电子电流和空穴电流与总电流的关系,参考(6-6)式,
,根据上一章的稳态分析中对电子电流和空穴电流与总电流的关系,参考(6-6)式,

此时多余载流子空穴的分布不变,参考(6-10),

可以计算得到(6-41)第二项的微分表达式,即
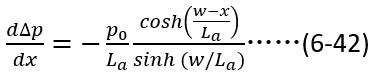
同时,很容易推导双极性扩散长度与空穴扩散长度之间的关系如下(过程省去,读者可以自行推导),
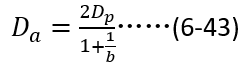
将(6-42)和(6-43)带入(6-41),就可以得到关断瞬间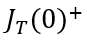 与
与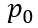 之间的关系为(令
之间的关系为(令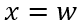 ),
),
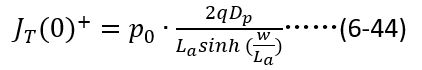
接下来,只需将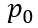 和
和 的关系带入(6-44),即可得出
的关系带入(6-44),即可得出 和
和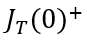 的关系。
的关系。
引用稳态分析中(6-11),即为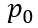 和
和 的关系,因为在这一瞬间,内多余载流子浓度分布并不会发生变化,即,
的关系,因为在这一瞬间,内多余载流子浓度分布并不会发生变化,即,
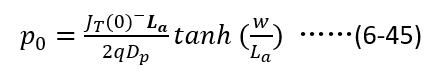
将(6-45)带入(6-44),即得到,

根据(6-46),关断瞬间电流突变的幅度取决于芯片厚度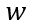 和扩散长度
和扩散长度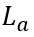 ,后者又取决于迁移率和载流子寿命。
,后者又取决于迁移率和载流子寿命。
令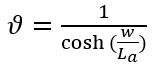 ,电流突变率,
,电流突变率,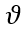 随芯片厚度
随芯片厚度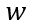 、迁移率
、迁移率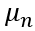 和载流子寿命
和载流子寿命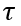 的变化趋势如下图所示:
的变化趋势如下图所示:

-
IGBT关断过程分析2024-07-26 6796
-
IGBT稳态分析—电流与电荷分布的初步分析(1)2023-12-01 1349
-
igbt怎样导通和关断?igbt的导通和关断条件2023-10-19 26373
-
米勒电容对IGBT关断时间的影响2023-09-05 3342
-
IGBT关断时的电流和电压2023-02-22 846
-
讨论一下IGBT的关断过程2023-02-13 2117
-
IGBT栅极电压尖峰分析2021-04-26 8510
-
大功率IGBT驱动的技术特点及发展趋势分析2021-04-20 4428
-
IGBT失效的原因与IGBT保护方法分析2020-09-29 5507
全部0条评论

快来发表一下你的评论吧 !

