绕组磁势谐波产生的原因和机理

 

 

前几期文章介绍了整数槽绕组的磁势。通过讲解我们了解到，绕组的磁势除了基波外还包括了一系列谐波，那么这些谐波磁势产生的原因是什么？机理如何？这些谐波的大小又与哪些因素有关？如何才能削弱甚至消除这些谐波呢？接下来的两期，就把这些问题掰开了揉碎了详细分析一下。本期先讲磁势谐波产生的原因和机理。

1 绕组的电流层分布与磁势

1.1 相关概念

绕组的磁势是绕组的导体中通以电流而产生的，因此绕组的磁势分布取决于导体电流的分布。电机绕组是由一些沿气隙圆周分布的导体以某种方式连接而成的。当绕组中通以电流时，沿气隙圆周就出现了一个“电流层”，这个电流层中各点的电流分布情况就决定了磁势波的分布。为了描述这个电流层的电流分布情况，我们引入一个新概念——“电流线密度”或称“安导强度”。定义气隙圆周某点处单位弧度上的电流总和为电流层在该点的“电流线密度”或“安导强度”。根据这个定义，如果是单层绕组，设气隙圆周上某一槽口宽度为θ(弧度)，θ=2π•[槽口宽度(米)/气隙圆周长]，槽内嵌有N根导体，每根导体中的电流i(安)，假定电流均匀分布于槽口上，则该处气隙圆周在整个槽口宽度θ范围的电流线密度为A=(i•N)/θ(安/弧度)，由于i•N的意义为安培乘以导体数，简称“安导”，因此有些文献和著作中也把“电流线密度”称为“安导强度”。如果是双层绕组，则i•N应为上、下层安导的代数和(上、下层电流方向相同时相加，否则相减)。由于齿顶范围内无导体，因此在齿顶范围内的安导强度应为零。由于不同槽内的导体可能分属于不同的相，在同一时刻不同的槽内导体中电流就不同，所以气隙圆周不同位置处的安导强度也不同，也就是说安导强度是沿气隙圆周分布的空间函数，因此把安导强度在整个气隙圆周上的分布称为“安导强度分布波”，简称“安导波”，它是一个空间函数，用A(x)来表示，其中变量x表示气隙圆周不同位置与坐标原点之间的弧度，单位是弧度，全圆周是2π。

以上是基于槽内安导均匀分布在槽口宽度范围内的情况，如果认为槽内的安导i•N，不是均匀分布于整个槽口宽度上，而是集中在槽口正中一点上，则θ→0而A→∞。这时每个槽产生的安导波变成一个冲激函数(数学中的δ—函数)，在槽口正中一点A=∞，而在其他各点A=0，且该函数沿气隙圆周在一齿距范围内的积分等于槽内的安导i•N。

小结一下：如果认为槽内安导均匀分布在槽口宽度范围内，则安导波A(x)就是沿气隙圆周分布的一系列矩形脉冲波，每个脉冲宽度为一个槽口的弧度范围，在该范围的函数值为A=(i•N)/θ (安/弧度)，每个齿顶范围的函数值为0；如果认为槽内安导集中在槽口中心一点，则安导波A(x)就是沿气隙圆周分布的一系列冲激函数，每个槽口中心的函数值为∞，其余范围函数值为0，函数在每个齿距范围的积分为该槽内安导。

这个“安导波”看起来与电机设计中的线负荷有些类似，它们都是反映气隙圆周上电流分布强度的物理量，但二者有着本质的区别：线负荷A是指电枢圆周上单位弧长上的电流，即A=∑(I•N)/C，其中：I为每根导体中的电流有效值；N为导体数；C为电枢圆周的周长，也就是说，线负荷是指气隙圆周上所有导体中的电流有效值之和(不考虑电流的方向和相位)除以整个气隙圆周的周长，单位是“安培/米”，对于一个特定的电机，当电枢电流一定时，线负荷就是一个定值，它反映了电机在某种负载条件下气隙圆周上电流层总的分布强度，从某种程度上代表了电枢表面的铜耗和电枢反应的强弱，因此电机的热负荷和电枢反应电抗等与线负荷有密切关系，是电机设计过程中的一个重要参数；而“安导波”A(x)是指电枢圆周某处单位弧度上的电流，它是一个空间函数，而不是一个定值。单位也与线负荷不同，安导波的单位是“安培/弧度”。安导波里的电流是指该处导体中电流的瞬时值，在任意固定时刻，由于交流绕组中各槽内导体的电流瞬时值不同，所以气隙圆周上各处安导强度也不同，因此“安导波”不是一个定值，而是一个沿气隙圆周分布的空间分布函数，代表了某时刻气隙圆周上不同位置处的电流分布强度。如果再考虑绕组中的电流为交流电流，则安导波还是时间的函数。由于这里我们只分析磁势的空间分布特征和空间谐波，因此可把时间设定为某一个特定时刻(t=t0时刻)，分析该特定时刻的安导波和磁势波，此时安导波和磁势波就仅是空间的函数。

1.2 安导波与绕组磁势的关系

根据上述安导波的定义可知，安导波沿气隙圆周某一段的积分等于该段弧上的净有总安导，即该段上所有各槽安导的代数和。取气隙圆周上磁场强度为零的一点作为坐标原点，通过坐标原点和坐标为x的任意一点取一闭合回路，如图1虚线所示。

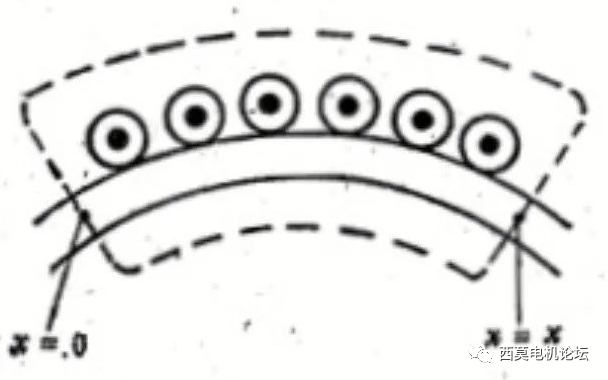
图1 磁势和安导的关系

则由全电流定律，沿闭合回路的总磁压降应等于回路内的总电流，即安导波沿弧段【0～x】范围的积分 ∫【0～x】A(x)dx。由于x=0点的磁场强度为零，因此该点的气隙磁压降为零，于是，在假定铁心的相对磁导率为无穷大，因而铁心中的磁压降可以忽略的条件下，闭合回路的总压降就等于x=x点处气隙的磁压降，称为x点的磁势，用符号F(x)表示。这样可得磁势波F(x)和安导波A(x)之间的关系为：

F(x)=∫【0～x】A(x)dx ⑴

上述分析中，是假定坐标原点的磁场强度为0的条件下给出的。由全电流定律可知，式⑴中的F(x)是相对于坐标原点的磁势，如果坐标原点磁场强度不为0，则还需要在式⑴的右侧加上x=0点的气隙磁压降才是x=x点的磁势绝对值。显然这并不改变整个磁势曲线的形状，只不过整个曲线向上或向下平移了一段距离而已。由于曲线形状不变时，曲线所包含的谐波成分不变，因此从谐波分析的观点看，坐标原点可以任意选取。

2 交流绕组磁势谐波产生的原因

2.1 产生正弦波磁势的条件

以上分析可知，当多相绕组通以多相电流时，在气隙中产生的磁势波由⑴式决定，为电流层中安导波的积分。由⑴式可见，欲使磁势波为正弦，则安导波的波形必须为正弦，而要想使安导波为正弦，则必须使气隙中每增加一个任意小的Δx，安导数都必须按照正弦(或余弦)的规律递增一个sin(x+Δx)-sin(x)，这意味着任意小的Δx内必须要有一个槽存在(有导体存在)，而且相邻两个槽中的安导数都不同，导体中的电流按照正弦规律变化。那么这将是一个什么样的绕组？通什么样的电流呢？首先任意小的Δx范围内都必须要存在一个槽，就意味着要有无穷多个槽，而无穷多个槽也就是没有了齿槽；其次任意两个相邻槽内导体的电流都不同则意味着在一对极距的范围内，每个槽内的电流相位都不同，即每个槽都属于不同的相，也就是说绕组的相数也是无穷多。这样在无穷多相绕组中通以无穷多相对称电流即可得到纯正弦波磁势。

小结一下：产生纯正弦波磁势的充要条件，一是槽数无穷多；二是相数无穷多；三是在这样的无穷多相绕组中，通以无穷多相的对称电流。满足上述三个条件就能产生正弦波磁势。显然这是一个理想的绕组，无穷多相电源也是一种理想电源。在实际的电机中通常是将绕组嵌放在有限的槽内，而且相数也是有限的，电源也不可能做到无穷多相。虽然也有些电机是无槽电机，但这并不能保证所有导体都是独立均匀布置在整个气隙中，至少导体还是有一定的粗细，线径不是无穷小，因此导体的分布仍然是离散的，至于绕组相数和电源相数则更不可能是无穷多。因此这种理想也只能是一个理想，实际电机中不可能实现，随之绕组的电势成为纯正弦也就变成了一种纯粹的理想。

2.2 多相绕组的合成磁势波

既然实际电机是在有限槽数内布置有限相绕组，那么它产生的绕组磁势必然不是纯正弦，不是纯正弦又会是什么样子的呢？

当多相绕组中所通的电流已知时，气隙圆周上的安导波即已知，根据式⑴就可以得到多相绕组的合成磁势波形图。

以三相对称单层绕组为例，绕组的参数为：三相、2极、12槽，q=2、Y=τ=6。假设每个槽内的安导集中分布在槽口中心一点，则根据式⑴，每过一个槽中心点，磁势就会跳变一个台阶，台阶的高度等于该槽内的安导代数和，台阶向上跳变还是向下跳变则取决于该槽内安导代数和的正负，正则向上跳变，负则向下跳变。这样就得到了三相绕组的合成磁势波形图，如图2所示。这是在A相绕组电流达到峰值时刻的绕组磁势波形图，需要顺便说明的是，不同时刻合成磁势的波形图是不同的，但这并不影响磁势的空间谐波次数和大小，对此将在下期详细讲解。

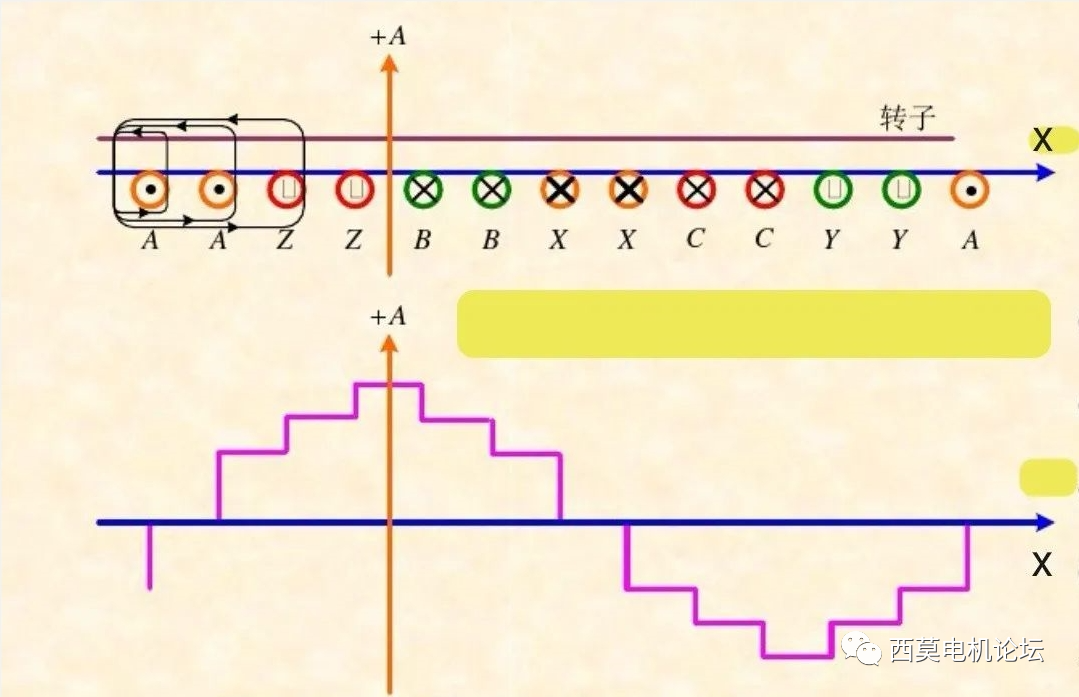
图2 三相单层绕组的合成磁势波

2p=2 q=2 m=3

由图2可见，这个单层绕组产生的磁势是一个阶梯波。从这个阶梯波上可以进一步看出：①每个极对数范围内台阶的数量为每对极的槽数；②相邻两个台阶的高度并不是按照正弦规律变化的，而是在一个相带(q个槽)的范围内，台阶的高度相同，不同相带的台阶高度不同。显然这个梯形波与基波正弦曲线相比，存在着差别，所以说，这种梯形波除了存在基波外，还存在着一系列谐波，这个梯形波与纯正的正弦基波之差就是这些谐波的总和，也正是由于上述两个原因才导致了谐波磁势的出现。对于第①个(阶梯)原因引起的谐波，我们称之为齿谐波；对于第②个(阶梯高度不按正弦变化)原因引起的谐波，我们称之为相带谐波。

2.3 齿谐波和相带谐波产生的机理

如前所述，根据产生磁势谐波的原因不同，可以把磁势谐波分为齿谐波和相带谐波。接下来我们就进一步把齿谐波和相带谐波分离，来看一看齿谐波和相带谐波到底是个什么模样。如图3所示为把合成的阶梯波磁势进一步分解为齿谐波和相带谐波的情况。

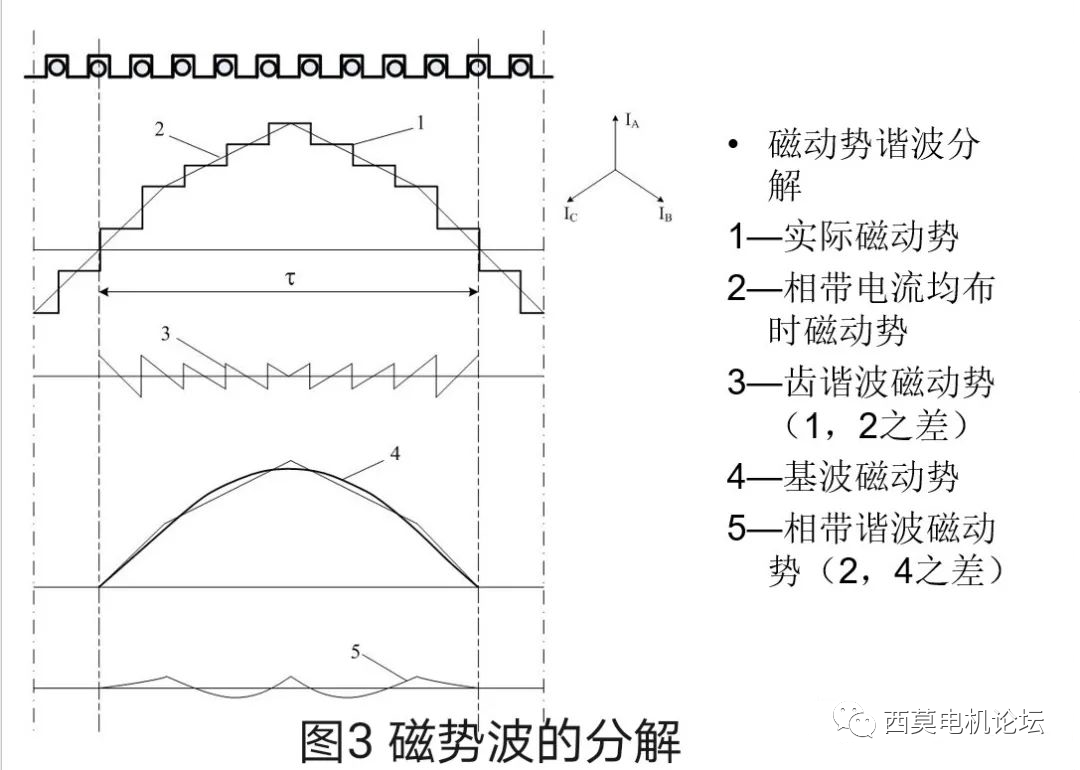
图3中，曲线1为实际的合成磁势波形，它就是图2中所示的阶梯波；曲线4为阶梯状合成磁势的基波，它是一条纯正弦曲线。曲线1包含了基波、齿谐波和相带谐波，也就是说曲线1所示的阶梯波是由基波、齿谐波和相带谐波相加而成的。

先说齿谐波产生的机理。齿谐波是由于阶梯的存在而产生的，而产生阶梯的原因是由于定子开有齿槽引起的，因此称其为齿谐波。当定子开有有限个齿槽时，安导波分布就不是连续的，而是集中在槽口中心点呈离散分布，从而使磁势产生阶梯。如果我们把槽数逐步增加，则阶梯个数就会随之增加，而相邻两槽产生的阶梯高度则随之变小，如果把槽数增加至无穷大，即q→∞，则阶梯就会消失了，随之齿谐波也就不复存在了，磁势就变成了曲线2的形状。

说完齿谐波再说相带谐波产生的机理。虽然曲线2中不存在了阶梯，也不存在了齿谐波，但由于相数仍然是有限的三相，在一个相带范围内，安导强度是相同的，而这个安导强度就代表了磁势的变化斜率，因此在一个相带范围内磁势增加的斜率是相同的，不同相带范围内由于安导强度不同而斜率也不同。正因如此，曲线2中存在着许多个折线段，折线段的数量取决于相带数，在一对极范围内，有多少个相带，就有多少段折线，而折线段的斜率则取决于该相带中的安导强度。曲线2这条折线，虽然不包含了齿谐波，谐波含量比梯形波小了许多，更接近了正弦基波，但它与正弦基波曲线相比仍然存在着差距，说明仍然存在着谐波，而这些谐波产生的原因是由于用折线逼近正弦曲线时，各段折线的斜率并不是完全按照正弦规律连续变化的，而是由于相带的划分而引起的各段折线斜率断续所造成的，因此称其为相带谐波。

综上所述，曲线2所示的折线已不包括齿谐波，但仍然包括相带谐波，也就是说，曲线2是相带谐波与基波之和。

如前所述，相带谐波是由于相数有限而引起的，如果在无穷多个槽的基础上逐步增加相数，则折线段的数量将随之增多，相数增多后每个相带的安导波都按正弦规律变化，则折线段的斜率也会按照正弦规律变化，这样相数越多，折线的形状就会越逼近基波正弦曲线，说明相数越多，相带谐波含量就越小。如果把相数增加到无穷大，则折线就变成了基波正弦曲线4了，此时就即不存在齿谐波也不存在相带谐波了。

归纳一下：

曲线1=基波+齿谐波加+相带谐波 ⑵      

曲线2=基波+相带谐波 ⑶

曲线4=基波 ⑷

将⑵式减去⑶式得到曲线3，曲线3即为齿谐波曲线，即：

曲线1-曲线2=曲线3=齿谐波 ⑸

将⑶式减去⑷式得到曲线5，曲线5即为相带谐波曲线，即：

曲线2-曲线4=曲线5=相带谐波 ⑹

由图3中的曲线3和曲线5可以看出齿谐波和相带谐波的形状。如果再进一步将曲线3和曲线5做傅立叶分解，就可以分别得到齿谐波和相带谐波所包含的谐波分量（略）。从两个曲线的形状定性地分析，可以看出，齿谐波的波长主要取决于齿距，波长约一个齿距的(Z1/p)±1次谐波最强烈，其余波长更短的谐波次数为k•(Z1/p)±1次，这是齿谐波的重要特征。相带谐波的波长主要取决于相带的宽度，波长约为一个相带宽度的2m±1次谐波最强烈，其余波长更短的谐波次数为2km±1次，这是相带谐波的重要特征。

简单总结一下齿谐波和相带谐波的产生机理：齿谐波是由阶梯引起，而阶梯的产生是由于定子开槽使安导波不连续，只在槽口中心跃变导致；相带谐波是由折线引起，而折线的产生是由于一个相带内的安导强度相同，磁势变化斜率相同导致。

本期介绍了绕组磁势谐波产生的原因，分析了相带谐波和齿谐波的产生机理，定性地分析了影响相带谐波和齿谐波的因素，并定性分析了相带谐波和齿谐波的基本特征。下期我们将继续深入分析相带谐波和齿谐波大小影响因素，并进一步讲解抑制和消除磁势谐波的方法及其机理。

　　审核编辑：汤梓红