

IGBT的关断瞬态分析—电荷存储变化趋势(3)
电子说
1.4w人已加入
描述
至此,我们完整地分析了关断瞬态过程中IGBT内部的空穴浓度分布变化从而引起的电荷存储变化,而电荷对时间的变化率即对应电流。(6-47)是通过泰勒展开的一阶近似得到的结果,而瞬态实际过程中需要更为精确的空穴浓度分布,才能获得精确的电压波形,下面我们对(6-47)进行修正。
首先,根据电荷守恒原则,先写出空穴的连续性方程如下(空穴的变化等于体外流入的电荷与体内复合的电荷之和):
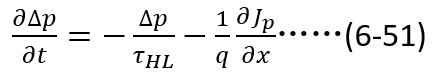
将(6-6)对 求导得到
求导得到 ,并代入(6-51),同时考虑到
,并代入(6-51),同时考虑到
1.IGBT器件内部电流处处相等,即 ,
,
2.大注入 ,化简即可得到双极型扩散方程,
,化简即可得到双极型扩散方程,

其中 。将(6-47)对时间求导,然后将(6-48)代入其中可以得到
。将(6-47)对时间求导,然后将(6-48)代入其中可以得到 ,
,

将(6-47)和(6-53)代入(6-52)得到扩散方程变形如下,

注,上述表达式中 的变量。
的变量。
将(6-54)对 两次求积分,即可得到
两次求积分,即可得到 修正表达式如下:
修正表达式如下:

系数 和
和 可以通过边界条件,
可以通过边界条件,  以及
以及 计算得到,如下,
计算得到,如下,

若将(6-56)代入(6-55),并分离 和
和 后可以得到
后可以得到
对比(6-47),显然(6-57)多了一些修正项。在某时刻 ,若对(6-57)从
,若对(6-57)从 积分,再乘以
积分,再乘以 ,则可以得到瞬态过程中更为准确的电荷总量,积分过程略去,结果如下,
,则可以得到瞬态过程中更为准确的电荷总量,积分过程略去,结果如下,

对照(6-49),(6-58)多了一个修正项 ,一般情况下,
,一般情况下,  ,那么(6-58)就趋近于(6-49)了。
,那么(6-58)就趋近于(6-49)了。
由此可以看出,空穴电荷浓度分布既与基区宽度 有关,也与基区宽度随时间的变化率
有关,也与基区宽度随时间的变化率 有关;而电荷总量则只与基区宽度
有关;而电荷总量则只与基区宽度 有关。
有关。
更进一步地,只要准确得知 与
与 的时间维度表达式,那么就可以得知任意时刻的电荷浓度空间分布以及该时刻的电荷总量与时间的关系,当然这就与外围拓扑电路相关,要得到具体的时间表达式,就需要针对不同的拓扑单独讨论。
的时间维度表达式,那么就可以得知任意时刻的电荷浓度空间分布以及该时刻的电荷总量与时间的关系,当然这就与外围拓扑电路相关,要得到具体的时间表达式,就需要针对不同的拓扑单独讨论。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
IGBT关断过程分析2024-07-26 6816
-
IGBT的关断瞬态分析—电荷存储初始值2023-12-01 1294
-
igbt怎样导通和关断?igbt的导通和关断条件2023-10-19 26400
-
米勒电容对IGBT关断时间的影响2023-09-05 3345
-
IGBT关断时的电流和电压2023-02-22 848
-
讨论一下IGBT的关断过程2023-02-13 2123
-
IGBT栅极电压尖峰分析2021-04-26 8512
-
大功率IGBT驱动的技术特点及发展趋势分析2021-04-20 4429
-
IGBT失效的原因与IGBT保护方法分析2020-09-29 5509
-
电机转速异常,如何快速分析出占空比变化的趋势2018-11-01 5656
全部0条评论

快来发表一下你的评论吧 !

